Алгоритм решения линейного уравнения

1. Записать характеристическую систему.
2. Найти систему п независимых первых интегралов

.

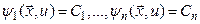1. Построить общий интеграл системы 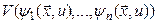, где V - произвольная функция.
2. Найти частное решение, удовлетворяющее условию (9).

Линейное уравнение с частными производными первого порядка может оказаться неразрешимым в окрестности характеристической точки и в том случае, когда каждая характеристика пересекает начальную поверхность 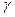ровно один раз.

Пример 1. Рассмотрим следующую задачу Коши:

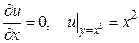. (10)

Характеристическим векторным полем здесь является постоянное единичное ноле (1, 0), характеристиками — прямые у = С, каждая из которых пересекает кубическую параболу 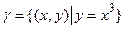ровно в одной точке. Продолжая начальную функцию 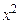(равную 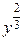на 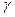) постоянной вдоль характеристик, т.е. независимой от х, получаем "решение" 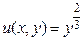— функцию, не являющуюся непрерывно дифференцируемой на прямой у = 0.

Возражение, что тем не менее найденная функция имеет частную производную по х и, следовательно, удовлетворяет уравнению, легко снять, сделав в задаче (10) замену переменных 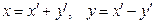. После этого поворота (и растяжения осей) получим следующую задачу Коши:

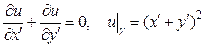
Полученное же "решение" 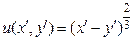не будет иметь частных производных ни 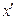по ни по 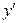на прямой 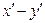= 0.

Пример 2. Решим уравнение

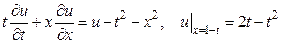. (11)

Составим характеристическое уравнение

.

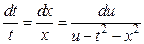Найдем два первых интеграла:

первый имеет вид 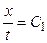, (12)

чтобы найти второй, воспользуемся свойством сложения пропорций ,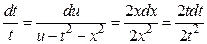

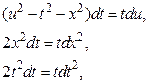
выполним почленное сложение 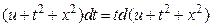в результате получим первый интеграл

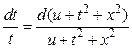или 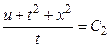. (13)

Общее решение уравнения можно записать в виде

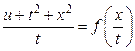, или ,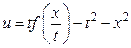

где 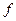- произвольная функция.

Чтобы решить задачу Коши, подставим в первые интегралы соотношение (11)

.

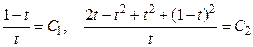Исключим здесь 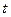и установим соотношение между 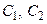, тогда из первого 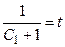, подставим во второе

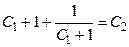. (14)

Подставляя в (14) вместо 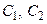первые интегралы (12), (13) и получим искомое решение задачи Коши.

.

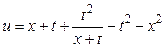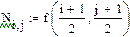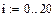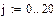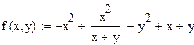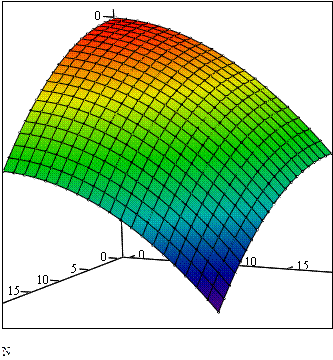
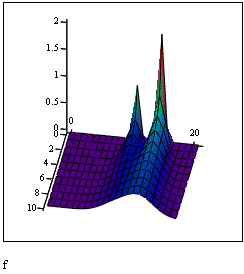
Построение поверхности в пакете Mathcad:

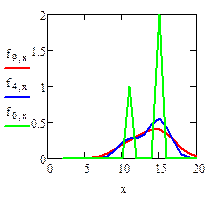
Численное моделирование процесса распространения

Загрязнения в водоёме без течения

Пример 3.Процесс диффузии примесей в воде или воздухе описывается уравнением диффузии:

,

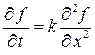где f- субъект загрязнения (соль, тепло, нефть, и т.п.). k- коэффициент диффузии, t- время, x- пространственная координата. Такого рода уравнение решается по следующей конечно-разностной схеме:

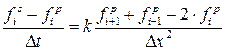или ,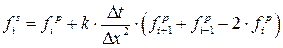

где индекс p- обозначает прошлый слой по времени, а s- следующий; индекс i- обозначает пространственную координату.

Варианты задач для самостоятельной работы

Для каждого уравнения найти:

1. общее уравнение поверхности, используя аналитическую теорию;
2. поверхность, проходящую через заданную линию;
3. выполнить построение поверхности в трехмерном пространстве;
4. составить дискретную модель и применить численное интегрирование;
5. провести сравнение численного и аналитического решения.

1.

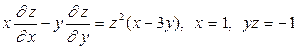
2.

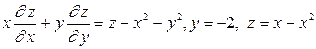
3.

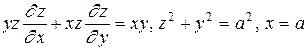
4.

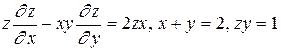
5.

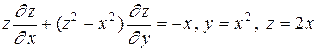
6.

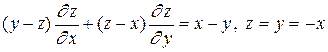
7.

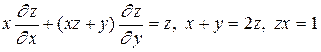
8.

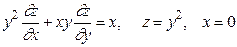
9.

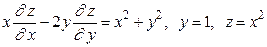
10.

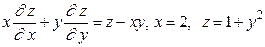
11.

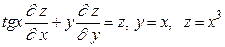
12.

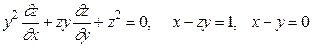
13.

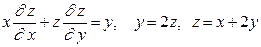
14.

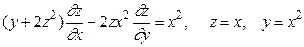
15.

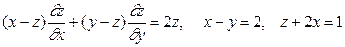
16.

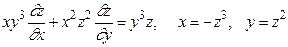
17.

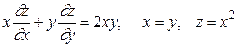
Теоретические вопросы, выносимые на экзамен

1. Предмет вычислительной математики. Математическое моделирование и вычислительный эксперимент.

2. Численные методы как раздел современной математики. Основные этапы решение задач на вычислительной техники.

3. Роль компьютерно ориентированных численных методов в исследовании сложных математических моделей. Понятие о разветвляющихся программах. Основные блоки. Циклические программы.

4. Действия с приближенными числами (абсолютная и относительная погрешности) Основная задача теории погрешностей.

5. Обратная задача теории погрешностей.