Экспоненциальная фильтрация

Рассмотрим задачу построения в реальном времени спектра сигнала, составленного из проекций сигнала в некоторой системе базисных функций.

В общем случае указанная задача формулируется как задача разложения сигнала в ряд

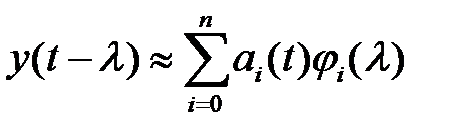, (2.1)

где 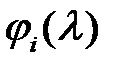‑ базисные функции;

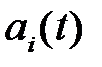‑ спектральные составляющие.

Ошибка разложения (2.1)

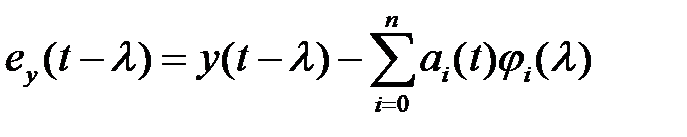. (2.2)

Определим экспоненциально-среднюю ошибку разложения (2.1)

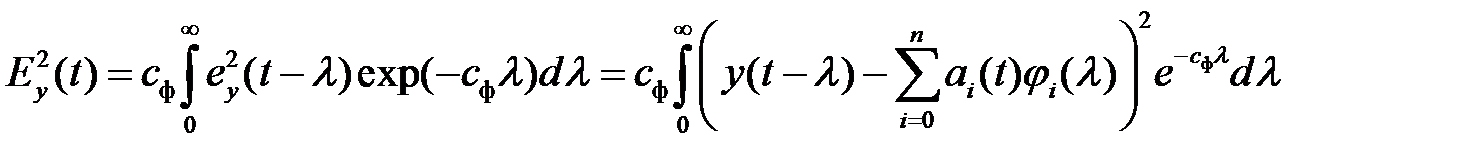. (2.3)

Здесь параметр 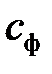играет роль показателя старения данных, обратная величина 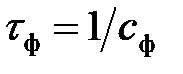имеет смысл постоянной времени фильтра первого порядка, на основе которого усредняется величина квадрата ошибки.

Ставится задача: определить неизвестные спектральные составляющие 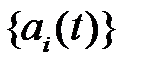сигнала 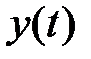из условия минимума экспоненциально-средней квадратичной ошибки (2.3):

.

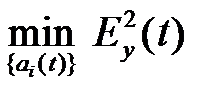Необходимые условия минимума квадратичной функции (2.3)

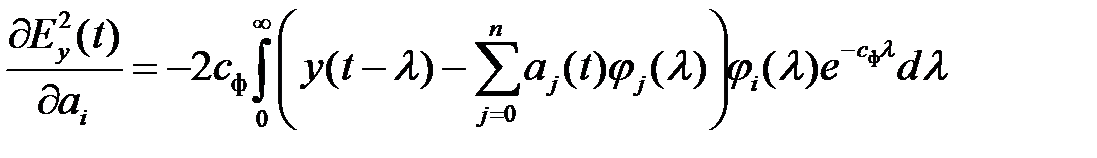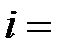, 0, 1, 2, ..., 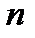. (2.4)

Система соотношений (2.4) представляет собой систему линейных алгебраических уравнений относительно неизвестных :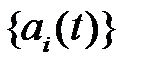

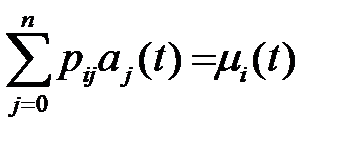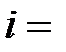, 0, 1, 2, ..., 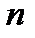. (2.5)

Здесь 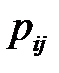‑ базовые корреляционные коэффициенты,

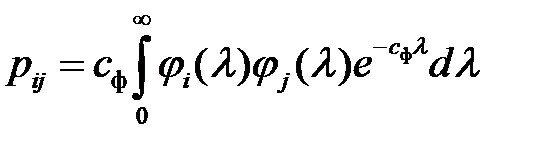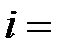; 0, 1, 2, . . . , 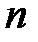; 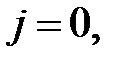1, 2, ..., 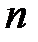. (2.6)

Величины 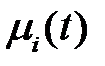являются моментами 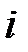-го порядка сигнала :

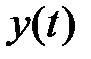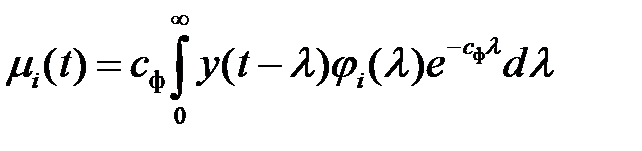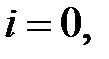; 1, 2, ..., 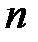. (2.7)

Запишем уравнения (2.5) в матричном виде

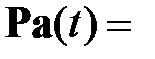μ , (2.8)

где

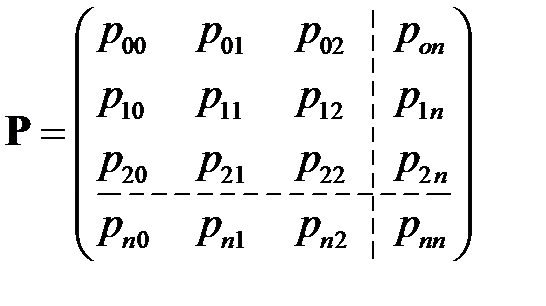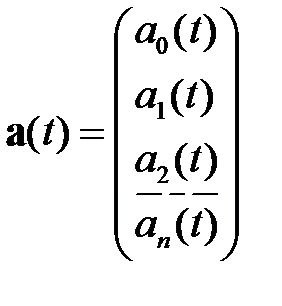, , μ .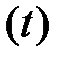

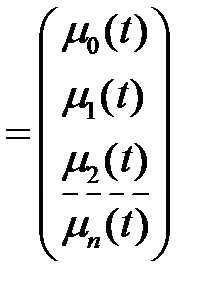Формальное решение уравнения (2.5):

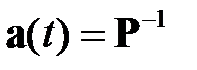μ 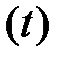, (2.9)

определяет базовую вычислительную формулу для оптимального анализатора спектра.

Таким образом, оптимальный анализатор спектра характеризуется матрицей корреляционных коэффициентов 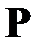, определяемой выбранной системой базисных функций 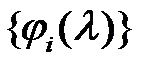. Процедура анализа состоит в вычислении моментов (2.7) анализируемого сигнала 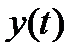с последующими вычислениями по формуле (2.9). Число анализируемых составляющих ‑ 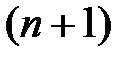, где 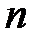‑ порядок анализатора.

В случае использования в анализаторе спектра ортогональной системы базисных функций 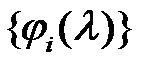, для которых выполняется условие ортогональности

,

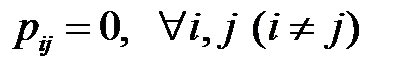формула анализатора (9) предельно упрощается:

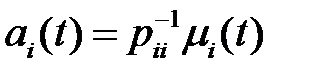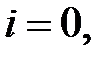, 1, 2, ..., 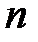. (2.10)

_____________________________

Рассмотрим вариант построения анализатора спектра на основе степенных функций[1].

Предположим, что задано базисное множество степенных функций:

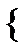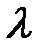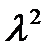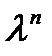
1, , , ..., 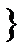. (2.11)

Для построения анализатора спектра необходимо вычислить корреляцонные коэффициенты базисных функций в соответствии с соотношениями (2.7):

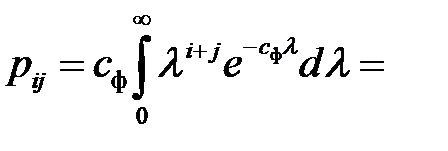
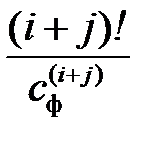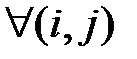, . (2.12)

Далее, соответствующие моменты входного сигнала будут равны

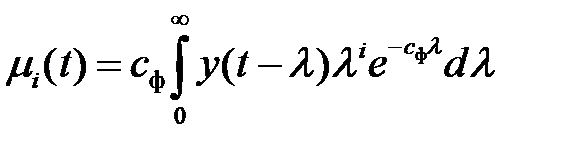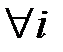, . (2.13)

Произведем замену переменных в соотношении (2.13):

.

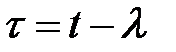Тогда выражение моментов входного сигнала (2.13) может быть представлено в другом эквивалентном виде

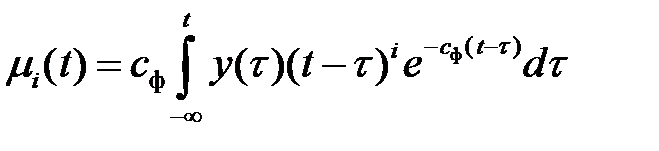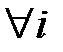, . (2.14)

Дифференцируя выражение (2.14) по времени 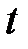, получим систему дифференциальных уравнений

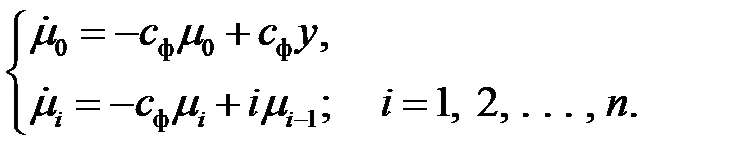(2.15)

Система дифференциальных уравнений (2.15) описывает фильтр, формирующий на своем выходе моменты 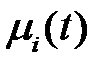входного сигнала 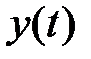. В совокупности соотношения (2.9), (2.12), (2.15) описывают работу анализатора спектра в базисе степенных функций. Структура анализатора спектра представлена на рис. 4.1.1.

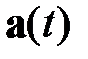μ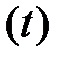

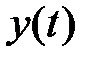Фμ

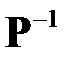Рис. 4.1.1. Структура анализатора спектра.

Здесь Ф_μ – формирующий фильтр моментов входного сигнала, 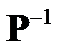‑ обратная матрица коэффициентов корреляции.

Построим уравнения формирующего фильтра (2.15) в дискретном виде. С этой целью воспользуемся процедурой дискретизации дифференциальных уравнений по неявному методу Эйлера.

Как известно, неявный метод Эйлера основывается на следующем дискретном представлении дифференциальных уравнений:

,

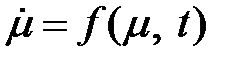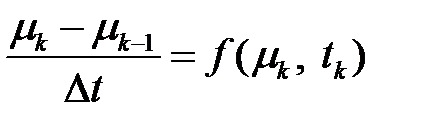(2.16)

где 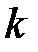‑ шаг интегрирования.

С использованием соотношения (2.16) систему дифференциальных уравнений (2.15) можно преобразовать в систему разностных уравнений

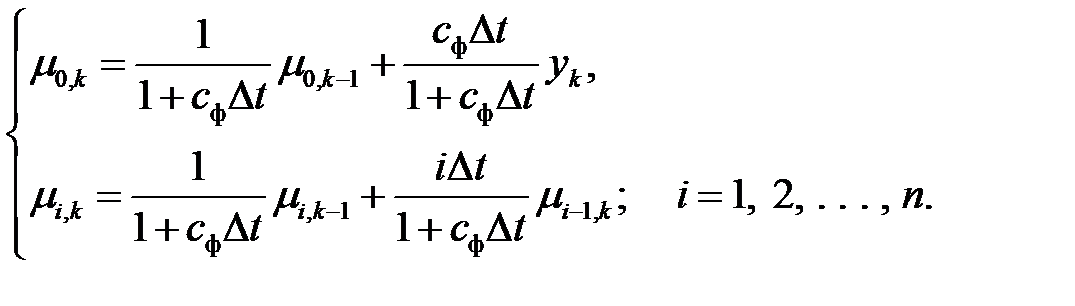(2.17)

Система разностных уравнений (2.17) определяет дискретный формирующий фильтр ‑ анализатор спектра.

Рассмотрим статистическую интерпретацию построенного анализатора.

С этой целью обратим внимание, что произведение 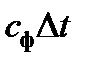в соотношениях (2.17) имеет смысл числа, обратного текущему числу статистических наблюдений:

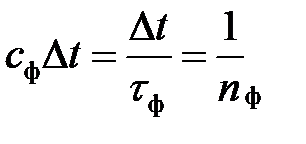, (2.18)

где 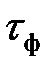‑ постоянная времени фильтра,

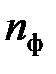‑ число статистических наблюдений, содержащихся в интервале времени, равном постоянной времени 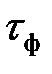, при дискретизации наблюдений с шагом .

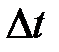С учетом (2.18) первое уравнение системы (2.17) можно представить в виде

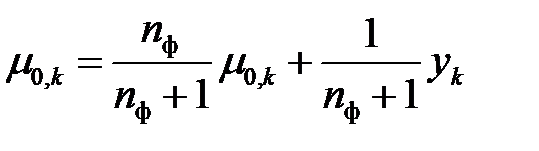. (2.19)

С другой стороны, текущее статистическое среднее величины :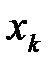

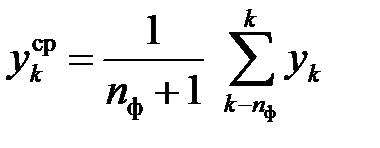, (2.20)

в рекуррентной форме совпадает с выражением (2.19):

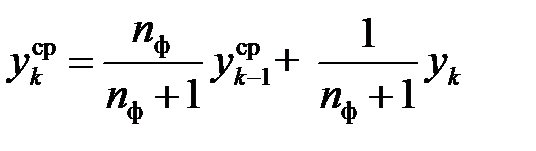. (2.21)

Таким образом 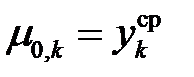. Аналогичные рассуждения можно провести и для остальных уравнений системы (2.17). В итоге можно показать, что анализатор спектра, построенный в соответствии с соотношениями (2.11), (2.12), (2.17), эквивалентен текущей аппроксимации процесса 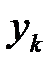полиномом:

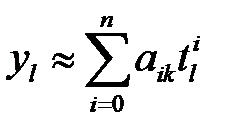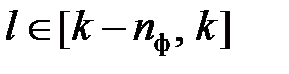, ; (2.22)

обычным методом наименьших квадратов.

Далее, можно показать, что построенный анализатор спектра эквивалентен наблюдателю переменных состояний динамической системы.

Действительно, рассмотрим текущее разложение сигнала 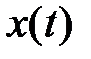в ряд Тэйлора

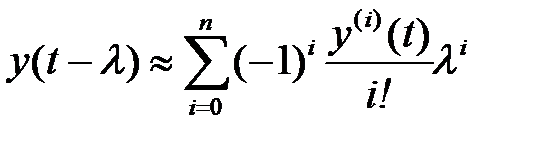, (2.23)

где 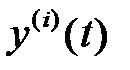‑ 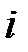-ая производная сигнала .

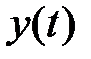Сравнение выражений (2.1), (2.11), и (2.23) позволяет определить равенства

,

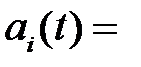
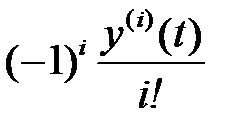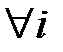
откуда

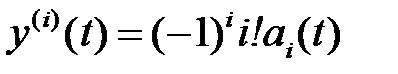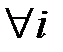, . (2.24)

Известно, что вычисление производных выходных реакций системы служит одним из способов определения состояний динамической системы. Отсюда следует, что построенный анализатор спектра можно рассматривать также как наблюдатель состояния динамических систем. При этом для иных форм представления состояний динамической системы, например, в базисе собственных функций, форма анализатора спектра соответствующим способом также меняется. Здесь в качестве базисных функций анализатора необходимо использовать собственные функции линейной динамической системы.

________________________________

Выработка управления в классической теории основывается на выявлении тенденций изменения ошибок управления, в частности, их интегралов и производных. При наличии помех в сигналах обратной связи и задающих воздействиях целесообразно использовать специальные анализаторы спектра, которые выявляют тенденции изменения ошибок управления на фоне помех.

Например, при выработке сигнала управления, пропорционального величине, интегралу и производной ошибки (ПИД-закон регулирования), может быть использован анализатор спектра на основе экспоненциальной фильтрации в полиномиальном базисе. Построенный анализатор спектра можно использовать для построения ПИД регулятора в соответствии с соотношениями

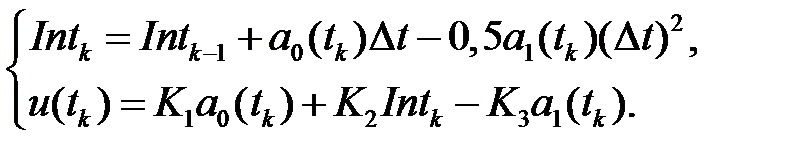(2.21)

Здесь 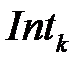‑ интеграл текущей ошибки регулирования; 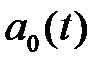‑ нулевая составляющая спектра ошибки, фактически ‑ значение ошибки после экспоненциального фильтра, 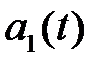‑ производная ошибки, вычисленная в экспоненциальном фильтре с обратным знаком, 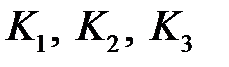– настраиваемые коэффициенты. Кроме того, к настраиваемым параметрам относится также постоянная времени экспоненциального фильтра .

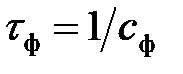Аналогично рекуррентное соотношение для экстраполирующего регулятора будет иметь вид

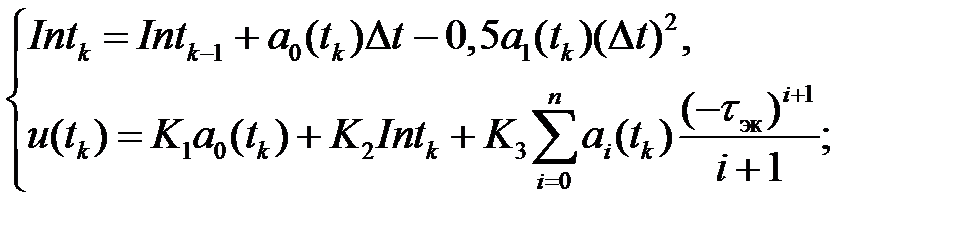(2.22)

где 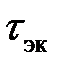‑ интервал экстраполяции. Здесь выражение при коэффициенте 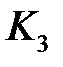представляет собой интеграл ошибки регулирования на текущем интервале экстраполяции [ ].

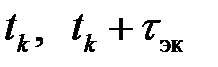В общем случае рекуррентное соотношение для регулятора будет иметь вид

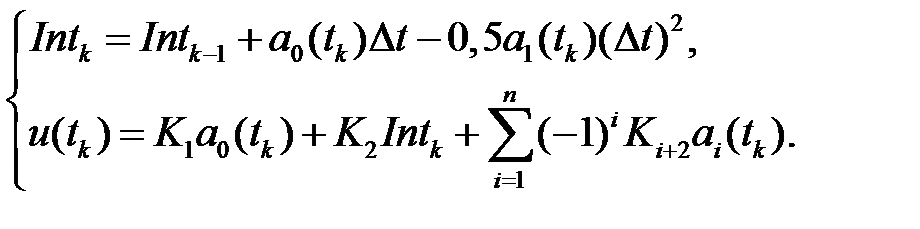(2.23)

Наблюдатели состояния

Для построения управления на основе пространства состояний необходимо проводить оценку в реальном времени вектора состояния объекта управления. Этой цели служат специальные наблюдатели состояния динамических систем.

Для линейных динамических систем:

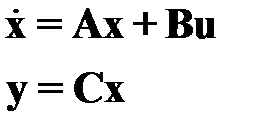, (2.24)

базовым является наблюдатель состояния

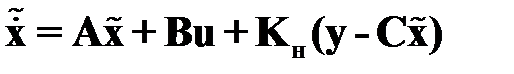, (2.25)

где 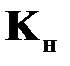‑ матрица коэффициентов наблюдателя.

Вычитая уравнение (2.25) из (2.24), получаем дифференциальное уравнение ошибки восстановления :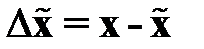

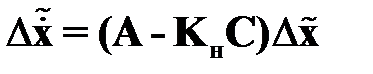. (2.26)

Если матрица коэффициентов наблюдателя 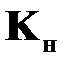подобрана таким образом, чтобы разность имела собственные числа с отрицательными вещественными частями, то решение уравнения (2.26) будет асимптотически устойчивым и ошибка восстановления 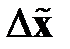будет стремиться к нулю. Соответствующим выбором матрицы 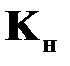можно добиться также определенных качественных показателей переходного процесса 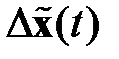по ошибке восстановления.

На основе наблюдателя (2.25) могут быть получены разные виды конкретных наблюдателей.

Так, при случайных возмущениях и помехах решение задачи наблюдения по критерию минимума среднеквадратической ошибки на основе оптимального выбора матрицы коэффициентов наблюдателя 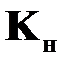получено Р. Калманом[2]. В этом случае матрица коэффициентов усиления наблюдателя 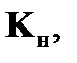определяемого по критерию минимума среднеквадратической ошибки наблюдения на фоне помех, определяется соотношением

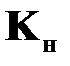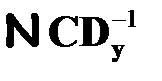= , (2.27)

где знакоопределенная положительная матрица удовлетворяет уравнению

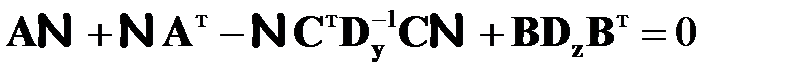. (2.28)

Здесь 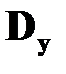, 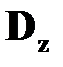‑ матрицы корреляционных моментов (дисперсий) случайных процессов ‑ шумов при измерении выхода системы 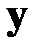и внешних возмущающих воздействий соответственно. При соотношениях (2.27), (2.28) наблюдатель (2.25) называется фильтром Калмана.

Практическая реализация фильтра Калмана основывается на модификациях его структуры в зависимости от конкретных условиях решаемой задачи. Обзор методов построения фильтров Калмана приводится в работе[3].

Оптимальное управление

Постановка задачи

Рассмотрим постановку задачи оптимального управления.

Пусть задан многомерный объект управления, динамические процессы которого описываются уравнениями

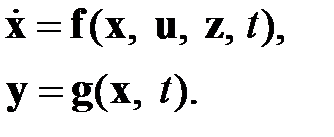(1.1)

Здесь, как и выше, 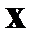‑ вектор переменных состояния, 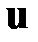‑ вектор управлений, ‑ вектор входных возмущающих воздействий, 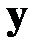‑ вектор выходных реакций.

Качество процессов управления в общем случае оценивается интегральным показателем, который может быть представлен как функционал потерь

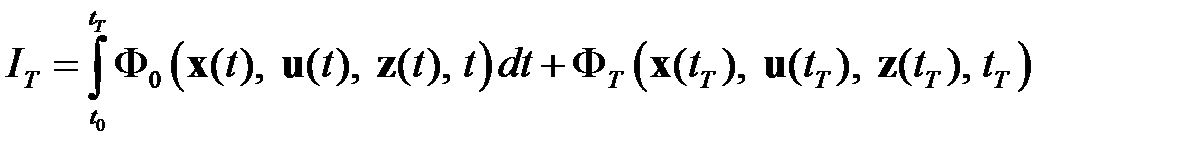, (1.2)

где 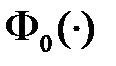‑ функция, оценивающая текущие потери для рассматриваемых процессов, 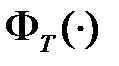‑ функция, оценивающая потери рассматриваемых процессов в терминальной точке 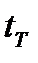. В целом показатель (1.2) состоит из двух составляющих: первая составляющая оценивает интегральные потери для процессов во временном интервале 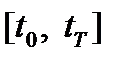, вторая составляющая оценивает потери для процессов в терминальной точке .

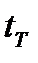Ставится задача: найти управление 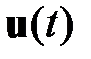динамическим объектом (1.1) из условия минимума интегрального функционала потерь (1.2).

Решение указанной задачи можно выполнить на основе двух подходов.

Первый подход основывается на двух этапах решения поставленной задачи. При этом на первом этапе, исходя из инженерного опыта, интуиции, знаний, определяется структура системы управления. На втором этапе осуществляется оптимизация управления в рамках заданной структуры.

Второй подход основывается на аналитической оптимизации самого управления 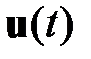. В этом случае используется математический аппарат нахождения экстремума функционала (1.2) при наличии ограничений (1.1).

Рассмотрим в начале первый подход к решению задачи оптимизации управления.

Предположим, например, что структура системы управления задана в виде системы с отрицательной обратной связью, представленной нарис. 4.2.1.

ур

+

Δy

–

у

у

Δх

u

z

u

x

Фн

К

f

g

Рис. 4.2.1. Структура системы управления по отклонению с наблюдателем

Здесь Ф_н – наблюдатель разности желаемого и текущего состояния объекта управления, построенный тем или иным способом. Будем полагать, что наблюдатель является линейной динамической системой. В силу линейности наблюдателя для него будут справедливы соотношения:

х = Ф_н(у), х_р= Ф_н(у_р),

где у_р, х_р – расчетные значения задающего воздействия и состояния объекта управления.

Отсюда следует

Δх = х_р– х.

Управление объектом формулируется обычно как функция переменных состояния объекта, его фазовых координат. В линейном случае такое управление можно представить в виде

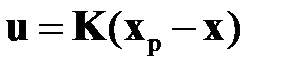, (1.3)

где 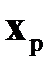‑ расчетное состояние, 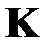‑ матрица коэффициентов, в общем случае нестационарных.

Подставляя (1.3) в (1.1), (1.2), получим соотношения для решения задачи оптимизации:

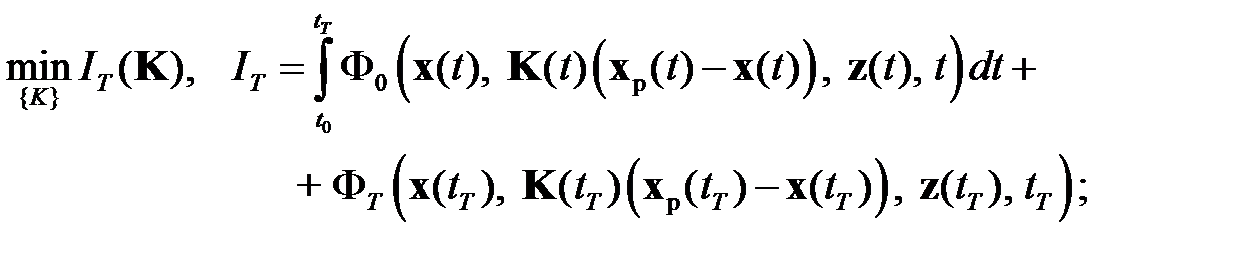(1.4)

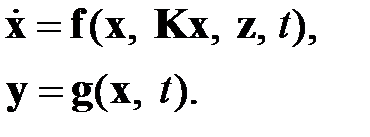(1.5)

Одним из подходов к решению задачи (1.4), (1.5) является следующий.

Создается экспериментальная физическая модель либо вычислительная модель системы управления, состоящая из модели объекта управления (1.5), регулятора (1.3) и подсистемы вычисления функционала потерь качества управления (1.4). В итоге функционал потерь будет обычной функцией 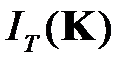многих переменных 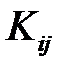, которые составляют матрицу коэффициентов .

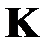Задача (1.4) решается в общем случае итерационными методами. В качестве примера итерационных методов рассмотрим ниже основную идею градиентного метода поисковой оптимизации.

Пусть на 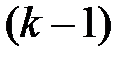-ом шаге решения задачи определено некоторое значение матрицы 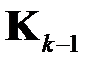. На основе экспериментов с вычислительной моделью задачи (1.4), (1.5) строится линейная аппроксимация

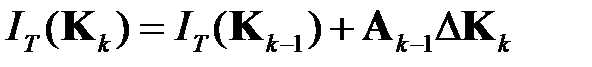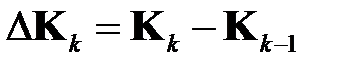, ; (1.6)

где 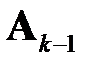‑ матрица коэффициентов аппроксимации.

Уточненное значение матрицы 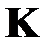на шаге 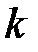определяется соотношением

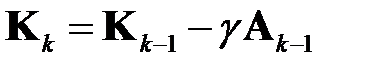, (1.7)

где 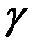‑ коэффициент релаксации.

Коэффициент релаксации 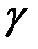определяется из условия

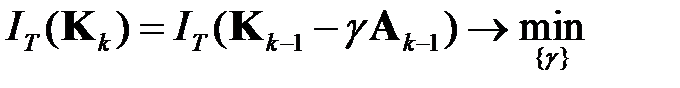. (1.8)

Задача (1.8) представляет собой задачу минимизации функции 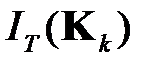по одному параметру ‑ 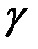. Такая задача решается достаточно просто. Для ее решения существуют эффективные алгоритмы, например, упорядоченного перебора вариантов.

В результате решения задачи (1.8) будет получено уточненное значение матрицы 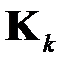и решение может быть итеративно продолжено.

Итерационный процесс решения задачи (1.4), (1.5) сходится при выполнении условия

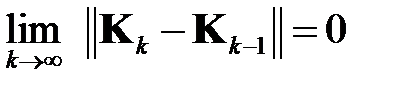. (1.9)

Практическим условием сходимости является

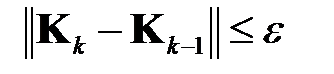, (1.10)

где 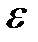‑ достаточно малое положительное число.

В итоге будет получено решение задачи (1.4), (1.5).

_______________________________________________

Второй подход к решению задачи минимизации функционала (1.2) при ограничении (1.1) состоит ваналитическом определении оптимального управления .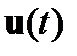

Решение поставленной задачи можно найти математическими методами, так как она представляет собой типовую задачу определения экстремума функционала при наличии ограничений.

Классический подход к нахождению экстремума функционала (1.2) при ограничении (1.1) является сведение задачи на условный экстремум к задаче нахождения безусловного экстремума на основе неопределенных множителей Лагранжа. Соответствующий функционал с множителями Лагранжа для интегральной составляющей функционала потерь:

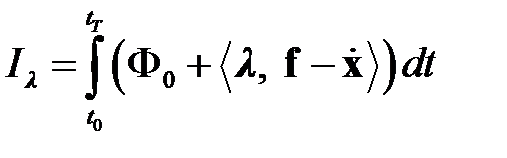, (1.11)

здесь λ – вектор неопределенных множителей Лагранжа,

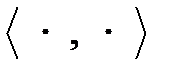‑ скалярное произведение векторов.

Введем обозначение

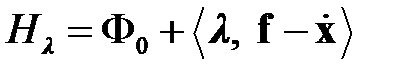. (1.12)

Из вариационного исчисления[4] известно, что необходимые условия минимума функционала (1.12) определяются соотношениями

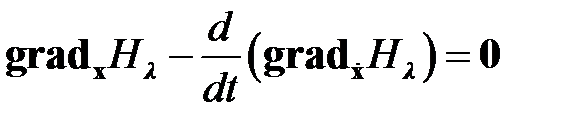, (1.13)

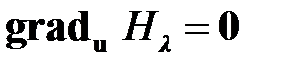, (1.14)

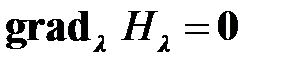. (1.15)

Уравнения (1.13) ‑ (1.15) представляют собой уравнения Эйлера, определяющие необходимые условия минимума функционала Лагранжа (1.11). Здесь 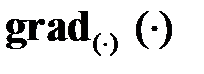‑ градиент скалярной функции по векторной переменной (т. е. вектор частных производных).

Уравнение (1.13) определяет необходимые условия минимума функционала (1.11) при незакрепленных граничных условиях. При задании конечных условий данные уравнения дополняются соотношениями

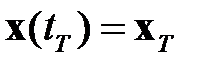
или

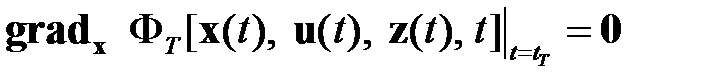. (1.16)

Уравнения (1.13)‑( 1.16) представляют собой исходные уравнения для аналитического решения задач оптимального управления.

При решении задач оптимального управления уравнения Эйлера часто записываются в форме, аналогичной уравнениям Гамильтона в аналитической механике. Это выполняется путем определения соответствующей функции 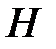аналогично так называемому гамильтониану

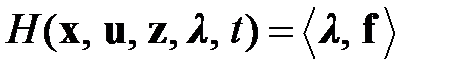. (1.17)

Здесь вектор 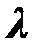отличается от вектора множителей Лагранжа в уравнении (12) тем, что имеет нулевую составляющую равную единице: 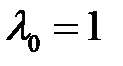. Подобным образом векторное представление 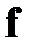в уравнении (1.17) отличается от соответствующего векторного представления правых частей уравнений динамики объекта тем, что имеет нулевую составляющую, равную подынтегральному выражению 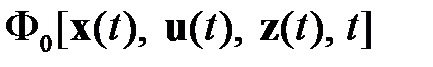, функционала (1.17):

.

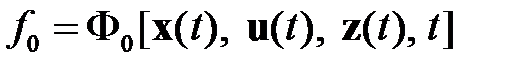Таким образом, вектора 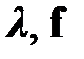теперь являются расширенными на нулевую составляющую и имеют размерность .

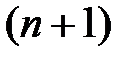В связи с изложенным первое необходимое условие оптимальности в случае «незакрепленных» конечных условий для переменных состояния можно записать посредством 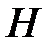в виде

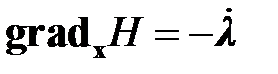, (1.18)

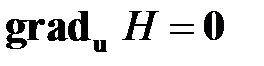, (1.19)

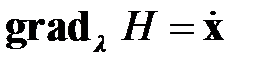. (1.20)

при граничных условиях 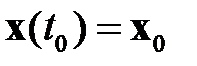и 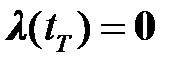. При задании конечных условий для 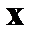последнее граничное условие заменяется: .

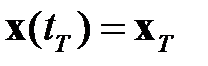Уравнения (1.18)‑( 1.20) называются уравнениями Эйлера-Гамильтона в канонической форме. Решение указанных уравнений позволяет найти управляющее воздействие 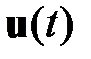, которое минимизирует функционал потерь.

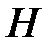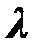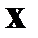Интерпретация постановки задачи оптимизации в терминах аналитической механики следующая. Гамильтониан характеризует полную энергию механической системы, а и аналогичны соответственно моменту и обобщенным координатам. Так как 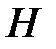представляет полную энергию системы, 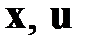следует выбирать из условия минимума (максимума) в каждый момент времени функции 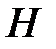. Это условие дает уравнение (1.19). Уравнения (1.18), (1.19) представляют собой уравнения движения системы в аналитической механике Гамильтона.

Понтрягиным Л.С.[5] в терминах уравнений аналитической механики была дана постановка задачи оптимального управления, которая сводит задачу к оптимизации некоторой координаты. В соответствии с принципом оптимальности Понтрягина, вводится нулевая координата

,

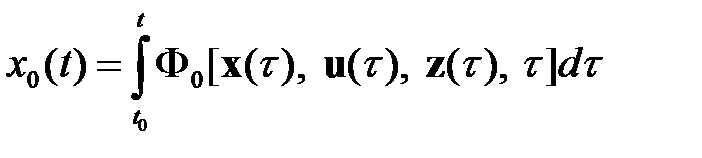так что 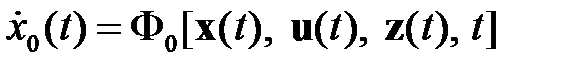. Оптимизация 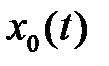в момент времени 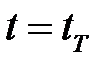соответствует оптимизации показателя потерь (качества), так как

,

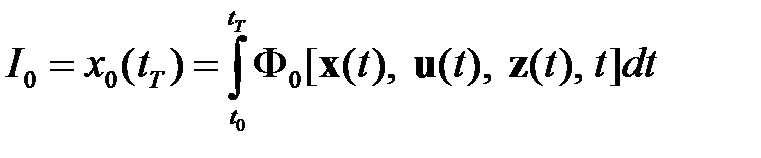что соответствует оптимизации исходного функционала потерь (качества).

Третий вариант аналитического решения поставленной задачи дает принцип оптимальности Беллмана[6].

В этом случае формулируется так называемая функция Беллмана

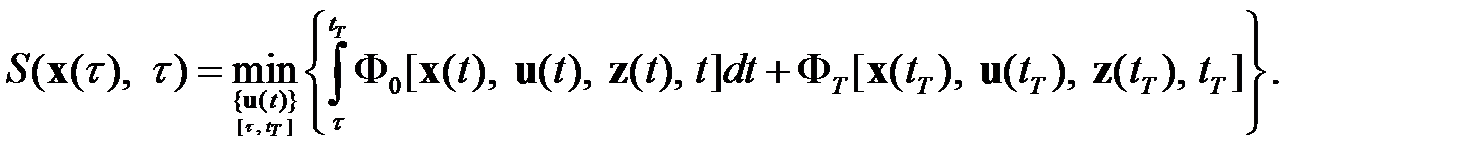(1.21)

Функция Беллмана представляет собой показатель потерь, минимизированный выбором оптимального вектора управления на произвольном интервале времени 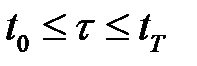. Функция 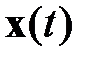, являющаяся решением уравнений

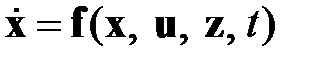(1.22)

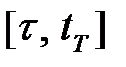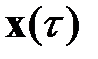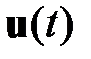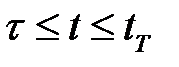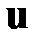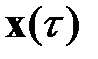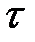на интервале , определяется ее начальным состоянием и управлением при . Поскольку оптимальное управление минимизирует функционал потерь, то устраняется зависимость правой части (1.21) от вектора управления , тем самым функция Беллмана зависит только от аргументов и . При этом обратим внимание, что при 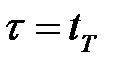функция Беллмана будет иметь значение

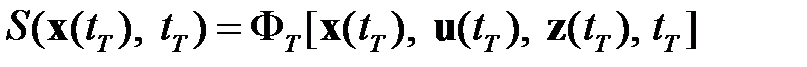(1.23)

Представим (1.21) в виде

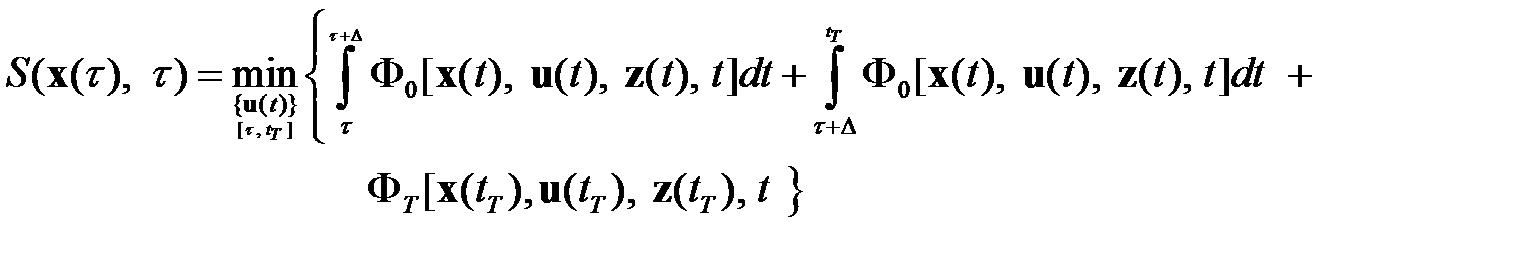(1.24)

Согласно принципу оптимальности Беллмана управление на каждом из последующих участков времени должно быть оптимальным независимо от состояния системы на предыдущих интервалах, т.е. при оптимально управлении функционал потерь должен быть минимальным и на участке 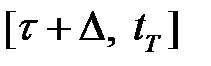. Это порождает рекуррентное соотношение для функции Беллмана, записанной в виде (1.24). Принимая условие, что отрезок времени достаточно мал, можно на основе эквивалентных математических преобразований и предельных переходов получить уравнение для функции Беллмана

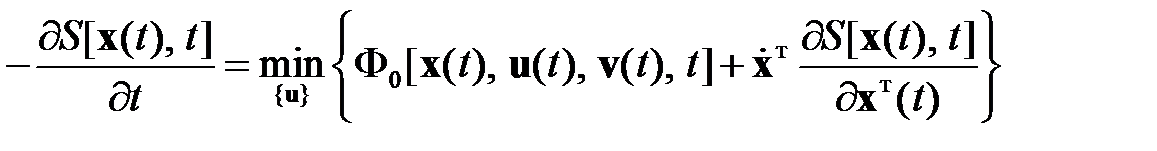, (1.25)

имеющее граничное условие (1.23). Решая уравнение (1.25), можно определить оптимальное управление, которое минимизирует функционал потерь.

Особенность рассмотренных аналитических подходов (1.21)‑( 1.25) состоит в том, что здесь постановки задач оптимального управления не содержат в качестве исходного требования отрицательной обратной связи по выходу объекта. Это связано с тем, что исходной базовой схемой управления здесь является не структурная схема с отрицательной обратной связью, принятая в инженерной практике, а теоретическая схема решения экстремальных задач с ограничениями, принятая в вариационном исчислении. Вследствие этого задачи оптимального управления здесь ориентированы на поиск прямого управления объектом без обратной связи. Решения задач управления с обратной связью здесь получаются лишь в случае, если удается в явном виде выразить зависимость управления от состояния объекта. Однако подобные решения могут оказаться непрактичными.

Типовые задачи

1⁰. Оптимальные линейные задачи

Предположим, что поведение объекта управления описывается уравнениями

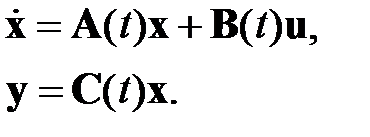, (2.1.1)

показатель потерь

,

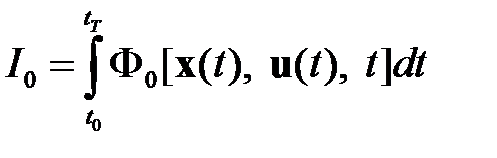где

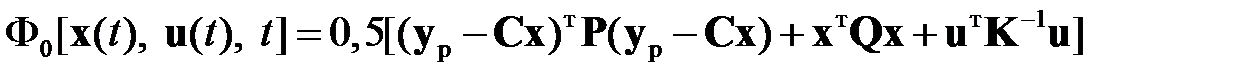. (2.1.2)

Здесь 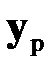‑ желаемое поведение системы; 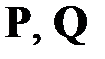‑ симметричные положительно-определенные матрицы, характеризующие веса предпочтений по минимизации ошибки движения системы 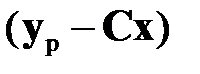и ее состояния 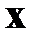; 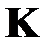‑ симметричная положительно-определенная матрица весовых коэффициентов, ограничивающих мощность управления.

В соответствии с уравнением (2.17)

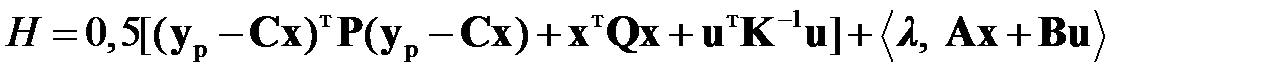. (2.1.3)

Из второго уравнения (2.19) имеем 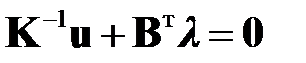. Тогда

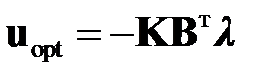. (2.1.4)

Выражение для оптимального управления (2.1.4) записано для вектора 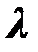. Необходимо выразить управление через вектор состояния .

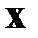Согласно уравнению (1.18) 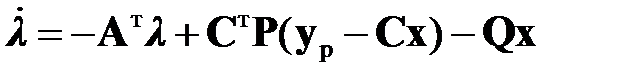. Из уравнения (2.1.1) после подстановки уравнения (2.1.4) имеем 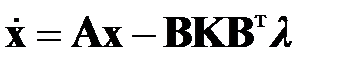. Последние два уравнения можно переписать в виде

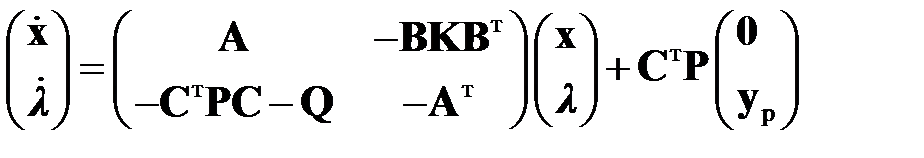. (2.1.5)

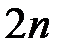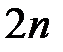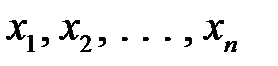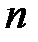Уравнение (2.1.5) состоит из линейных дифференциальных уравнений первого порядка, содержащих неизвестных ; . Они подчинены граничным условиям при 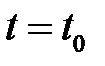: 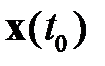= 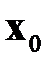, а также 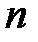граничным условиям на конце интервала времени: либо 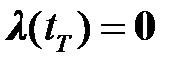, либо 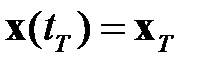в зависимости от постановки задачи. Решение уравнения (2.1.5) позволяет получить оптимальное управление 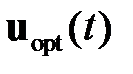в интервале времени .

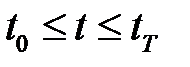Решение уравнения (2.1.5) невозможно осуществлять в реальном времени, так как оно зависит от граничных условий в двух точках: начальной и конечной. Более того, оптимальное управление зависит от значений вектора состояния, которые в соответствии с уравнением (2.1.5) необходимо знать с упреждением. Подобное управление физически нереализуемо. Поэтому данное решение следует рассматривать как решение задачи планирования управления. Полученный план оптимального управления в дальнейшем можно использовать для разомкнутого управления реальным объектом либо использовать стратегию модельно-упреждающего управления.

Рассмотрим вопрос разделения двухточечной краевой задачи, которую представляет собой задача (2.1.5) в две одноточечные задачи, из которых одна решается в реальном времени, а вторая с упреждением во времени[7].

С этой целью введем линейную связь между векторам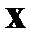и и 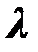, обусловленную уравнением (2.1.5)

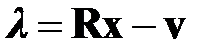, (2.1.6)

где 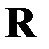‑ квадратная матрица коэффициентов усиления, в общем случае переменных; ‑ переменный вектор.

Подстановка соотношения (2.1.6) во второе уравнение (2.1.5) дает

.

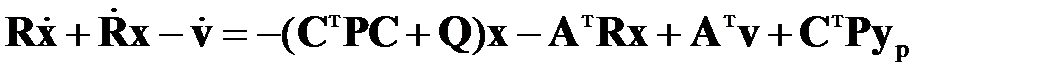Далее, подстановка 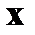из первого уравнения (2.1.5) с учетом соотношения (2.1.6) приводит к уравнению

.

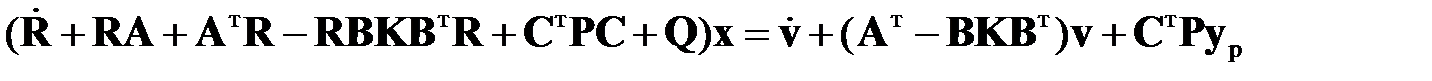Так как это выражение должно выполняться для всевозможных 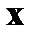, то условием этого служат уравнения

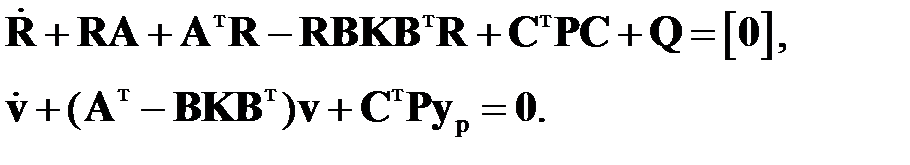(2.1.7)

Здесь первое уравнение представляет систему нелинейных дифференциальных уравнений первого порядка типа Риккати. Второе уравнение (2.1.7) является системой линейных дифференциальных уравнений первого порядка, сопряженной к уравнениям системы, замкнутой по управлению. В случае отсутствия ограничений на 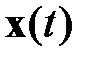в конечной точке 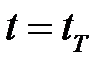краевое условие принимается 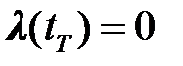. Тогда граничные условия, накладываемые на 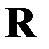и в соответствии с уравнением (2.1.6), состоят в равенстве нулю элементов 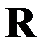и в конечной точке .

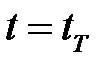Определив 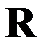и , можно получить закон управления оптимальной системы в результате подстановки уравнения (2.1.6) в уравнение (2.1.4):

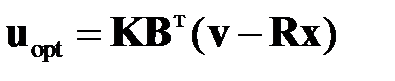. (2.1.8)

Преобразуем полученную систему управления к типовому виду системы управления с обратной связью.

С этой целью произведем замену переменных во втором уравнении (2.1.7)

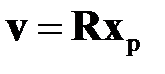, (2.1.9)

где 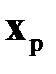‑ расчетное значение вектора состояния .

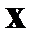При заданном соотношение (2.1.9) представляет собой систему линейных алгебраических уравнений. Если определитель системы уравнений (2.1.9) отличен от нуля, то система уравнений имеет однозначное решение

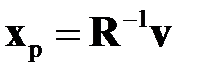. (2.1.10)

Если система уравнений недоопределена, то в качестве решения принимается, например, одно из базисных решений, свободные составляющие решения обнуляются.

При определенных 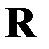и 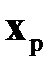закон управления оптимальной системы получается в результате подстановки соотношения (2.1.9) в (2.1.8):

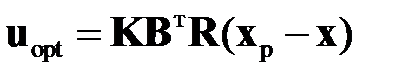. (2.1.11)

На рис. 4.2.2 представлена структура полученной оптимальной системы управления.

+ +

+

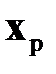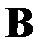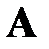Оптимальное планирование

Оптимальный регулятор

Объект управления

Рис. 4.2.2. Структура оптимальной системы управления

Интерпретация построенной структуры оптимальной системы управления следующая.

При решении задачи оптимального управления на стадии оптимального планирования осуществляется расчет матрицы коэффициентов усиления 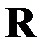и расчетного вектора состояний 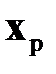. Оптимальное планирование сводится к решению краевых задач (2.1.10) в обратном времени от 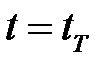к 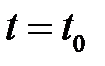при заданных конечных условиях.

После того как получены оптимальная матрица коэффициентов усиления 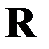и расчетный вектор состояний 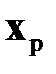, в реальном времени «вперед» от 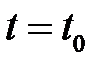к 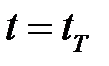решается задача оптимального регулирования состояния объекта управления с обратной связью по ошибке регулирования.

Таким образом, задача оптимального управления распадается на две последовательные стадии решения задачи: оптимального планирования и оптимального регулирования. Отметим, что полученный здесь формальный результат находится в полном соответствии с общей логикой решения задач системными методами: планирование операции (L2) и реализация операции (L3), если под операцией здесь понимать операцию по управлению объектом. Как и в общем случае, планирование операции управления здесь осуществляется в обратном времени, реализация операции – в реальном времени.

2⁰. Решение линейных задач методом динамического программирования

Рассмотрим синтез терминального управления линейным объектом

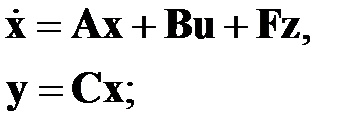, (2.2.1)

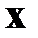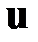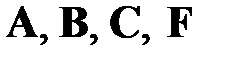где ‑ вектор состояния, ‑ вектор управления, ‑ вектор возмущений; ‑ соответствующие матрицы коэффициентов, в общем случае переменных во времени.

Функционал потерь рассматриваемой задачи имеет вид

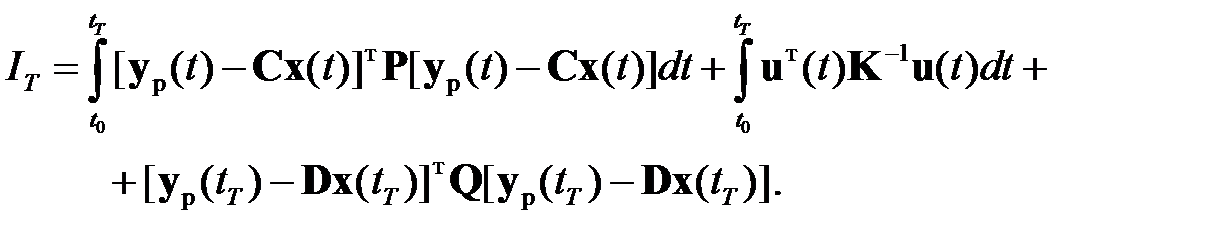(2.2.2)

На основе общего уравнения для функции Беллмана (1.25) с использованием соотношений (2.2.1), (2.2.2) получим уравнение для функции Беллмана в рассматриваемом случае

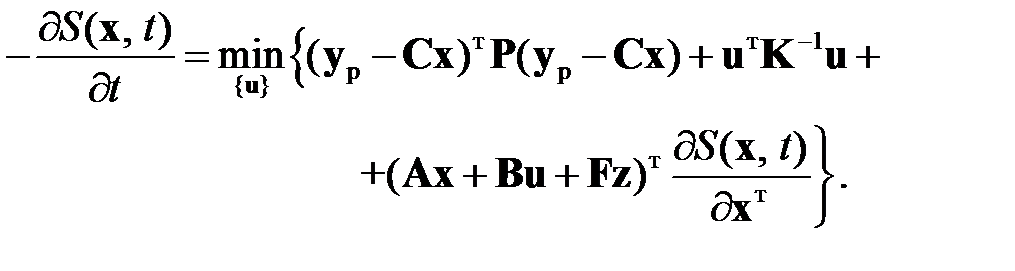(2.2.3)

Вынесем за знак операции минимума члены, не зависящие от :

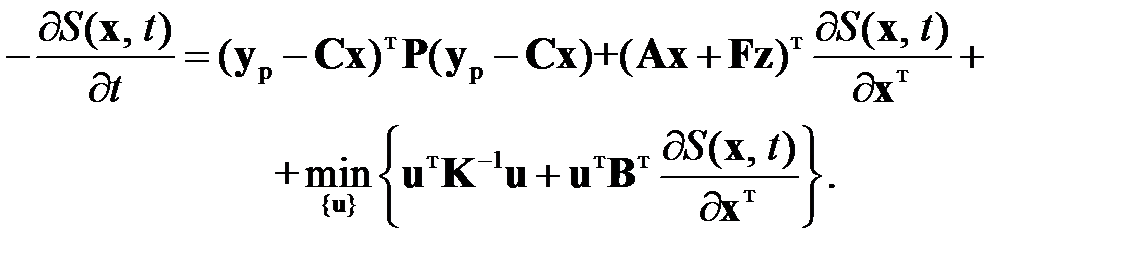(2.2.4)

Поскольку 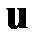не содержится в первых двух слагаемых, минимум рассматриваемого выражения можно отыскать, продифференцировав последнее слагаемое по вектору 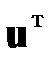и приравняв нулю результат дифференцирования. Тогда

,

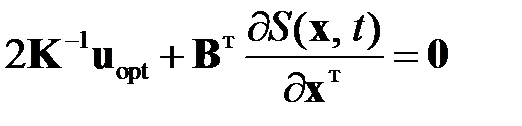где

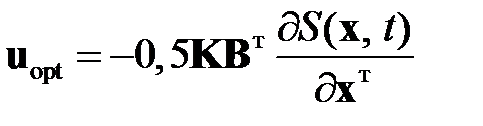(2.2.5)

представляет собой вектор оптимального управления.

Подставляя вектор оптимального управления в выражение функции Беллмана (2.2.4), получим

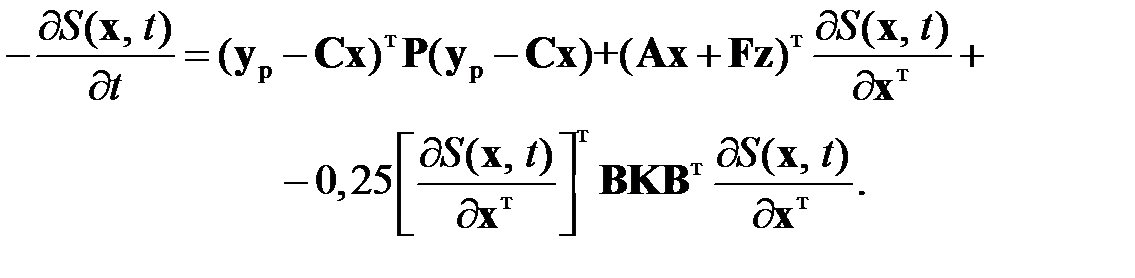(2.2.6)

Решение уравнения (2.2.6) ищется в классе квадратичных форм

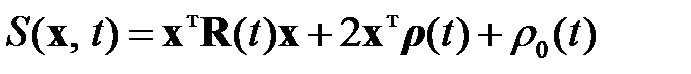, (2.2.7)

где 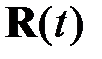‑ симметричная матрица коэффициентов, 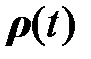‑ вектор-функция, 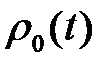‑ скалярная функция.

Из (2.2.7) следует

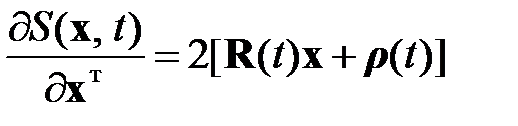. (2.2.8)

Подстановка квадратичной формы (2.2.7) в выражение (2.2.6) позволяет получить уравнения относительно неизвестных , :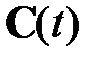

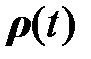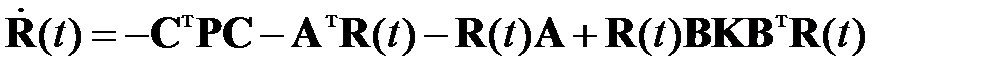; (2.2.9)

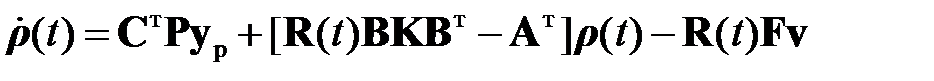. (2.2.10)

Граничные условия для уравнений (2.2.9), (2.2.10) можно получить на основании общего требования к граничным условиям функции Беллмана (1.23). Из (1.23) и (2.2.2) получаем

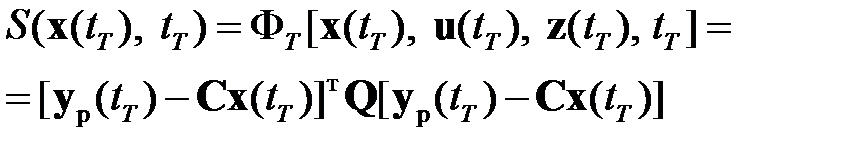. (2.2.11)

Сравнивая при 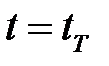выражения (2.2.7), (2.2.11), получим

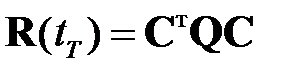; (2.2.12)

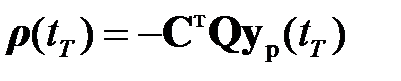. (2.2.13)

С учетом (2.2.5) и (2.2.8) вектор оптимального управления для линейного объекта (2.2.1) при наличии измеряемых возмущений представляется в виде

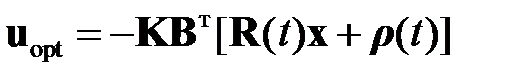. (2.2.14)

Здесь 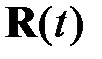и 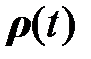определяются уравнениями (2.2.9), (2.2.10).

Как и в предыдущем примере для получения структуры системы управления с регулирующей обратной связью по отклонению произведем замену переменных

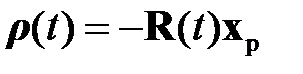. (2.2.15)

С учетом (2.2.15) оптимальное управление будет иметь вид

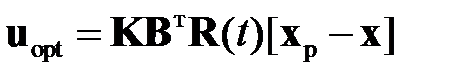. (2.2.16)

Рассмотрим вопрос устойчивости оптимальной системы.

С этой целью определим полную производную функции Беллмана по времени

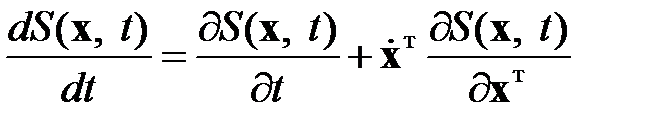. (2.2.17)

Обратимся к уравнению (2.2.3). Если 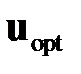, 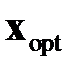‑ соответственно оптимальные управляющие воздействия и отвечающие им траектории координат объекта, то это уравнение можно представить в виде

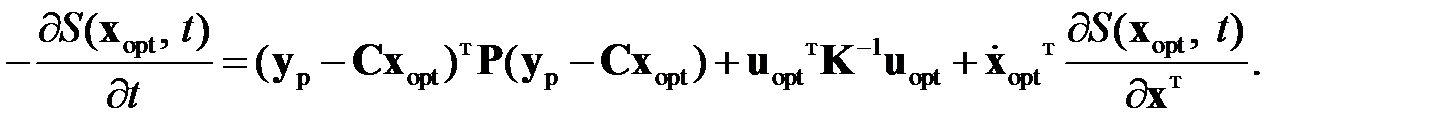(2.2.18)

Подставляя (2.2.18) в (2.2.17) получим

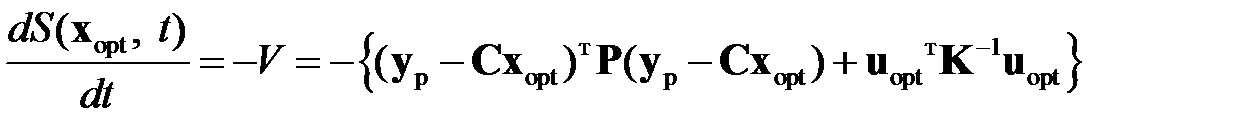. (2.2.19)

Так как 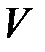‑ положительно определенная квадратичная форма, следовательно, 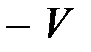‑ отрицательно определенная квадратичная форма. Поэтому функция V стремится с течением времени к минимуму. Данное условие является условием асимптотической устойчивости замкнутой системы управления. При этом функция 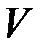выступает здесь как функция Ляпунова, которая лежит в основе метода Ляпунова оценки устойчивости динамических систем.

3⁰. Структура оптимального регулятора

Рассмотренные выше оптимальные законы управления линейным объектом построены на знании вектора состояния объекта. Однако в действительности вектор состояния непосредственно не наблюдаем, поэтому необходимо использовать специальные устройства – наблюдатели состояния, которые восстанавливают состояние объекта по результатам наблюдения. Таким образом, конструкция регулятора состоит из собственно регулятора + наблюдатель состояния.

Для построенной указанным образом системы регулирования справедливо следующее[8].

Пусть даны уравнения объекта, уравнение системы оценки его состояния и закон управления

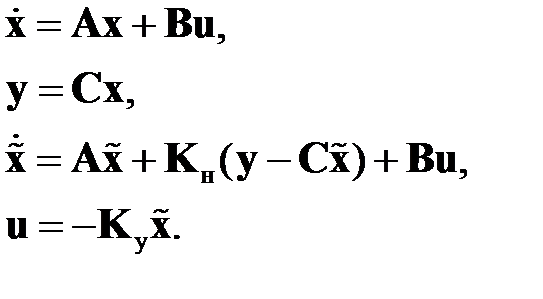(2.3.1)

Тогда характеристический многочлен 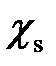замкнутой системы регулирования (2.3.1) в целом удовлетворяет уравнению

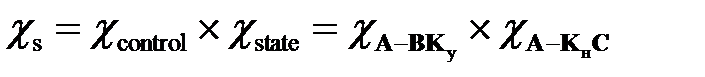. (2.3.2)

Доказательство данного положения весьма простое. Достаточно произвести замену переменных в уравнениях (2.3.1) по правилу: 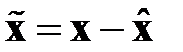. Это преобразование линейно и взаимно однозначно и, следовательно, не влияет на многочлен 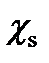. В новых координатах уравнения (2.3.1) примут вид

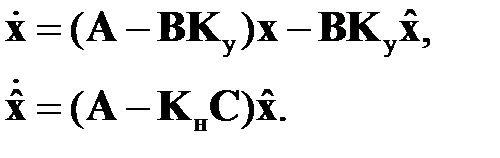(2.3.3)

Характеристический многочлен 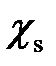является характеристическим многочленом матрицы, представляющей уравнения (2.3.3)

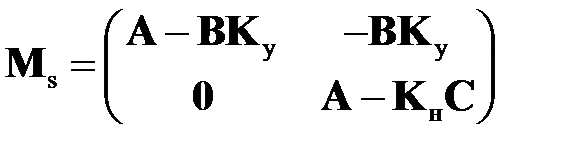. (2.3.4)