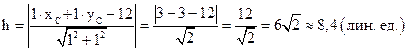Как аналитически задать прямую, проходящую через данную точку в данном

направлении, или через две данные точки, или в параметрической форме?

Как вычислить угол между прямыми, между плоскостями, между прямой и

плоскостью?

Сформулируйте условия параллельности и перпендикулярности плоскостей,

Прямых, прямой и плоскости.

Кривые второго порядка на плоскости

1. Какие кривые называют кривыми второго порядка?

2. Сформулируйте определение окружности, эллипса, гиперболы, параболы.

3. Напишите каноническое уравнение окружности, эллипса, гиперболы, параболы.

4. Сформулируйте свойства окружности, эллипса, гиперболы, параболы.

Методические указания

Линейная алгебра

ПримерПусть дана система линейных уравнений (1).

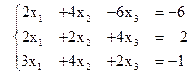(1)

Требуется найти решение этой системы методом полного исключения.

Запишем эту систему в виде прямоугольной таблицы, у которой в столбцах расположены коэффициенты при неизвестных, а в последнем столбце - свободные члены (после того, как их перенесли в правую часть уравнений). Эту таблицу будем называть "расширенная матрица системы".

Расширенная матрица этой системы имеет вид (2) .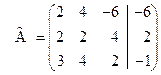

Первый шаг решения (I шаг) состоит в следующем.

1. Выбираем строку, у которой первый элемент не равен нулю (в нашем примере можно взять, например, первую строку). Эту строку назовем «разрешающая (ведущая) строка первого шага». Первый столбец назовем «разрешающий (ведущий) столбец первого шага», а элемент, расположенный на пересечении разрешающей строки и разрешающего столбца назовем «разрешающий (ведущий) элемент первого шага». Эта операция соответствует перемене местами уравнений системы, поэтому новая система будет равносильна исходной.

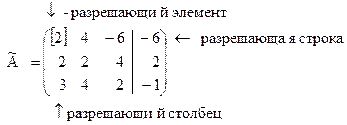
2. Разрешающую (первую) строку делим на разрешающий элемент. Получаем новую строку ( 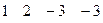), которую записываем первой строкой в новой матрице 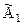. При этом первая строка новой матрицы матрица примет вид:

.

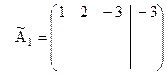3. Чтобы найти вторую строку матрицы 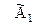,ко второй строке матрицы 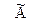прибавим новую первую строку из матрицы 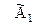, предварительно умножив ее на такое число, чтобы в первом столбце оказался ноль. В нашем примере ко второй строке матрицы 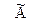нужно прибавить первую строку матрицы 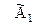, умноженную на (-2), получим: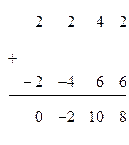

Теперь матрица 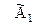будет иметь вид:

.

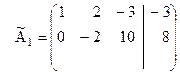4. Чтобы найти третью строку матрицы 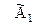,к третьей строке матрицы 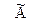прибавим новую первую строку из матрицы 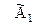, предварительно умножив ее на такое число, чтобы в первом столбце оказался ноль. В нашем примере ко второй строке матрицы 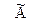нужно прибавить первую строку матрицы 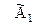, умноженную на (-3), получим: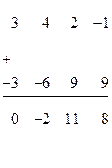

Теперь матрица 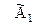будет иметь вид:

.

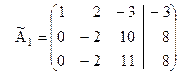Если матрицу 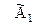будем рассматривать, как систему уравнений, то увидим, что в результате элементарных преобразований получили систему равносильную исходной, причем неизвестная 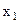в первое уравнение входит с коэффициентом единица, а из остальных уравнений она исключена.

Второй шаг решения (II шаг) состоит в том, что неизвестная 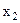исключается из всех уравнений кроме второго, а во второе должна входить с коэффициентом единица.

1. Выбираем любую строку, которая еще не была разрешающей, и у которой второй элемент не равен нулю (в нашем примере можно взять, например, вторую строку матрицы 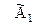). Эту строку назовем «разрешающая (ведущая) строка второго шага». Второй столбец назовем «разрешающий (ведущий) столбец второго шага», а элемент, расположенный на пересечении разрешающей строки и разрешающего столбца назовем «разрешающий (ведущий) элемент второго шага».

.

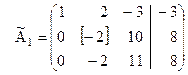2. Разрешающую (вторую) строку делим на разрешающий элемент. Получаем новую строку ( 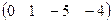), которую записываем второй строкой в новой матрице 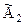. При этом новая матрица примет вид:

.

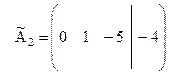3. Чтобы найти первую строку матрицы 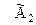,ко второй строке матрицы 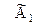прибавим новую вторую строку из матрицы 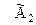, предварительно умножив ее на такое число, чтобы во втором столбце оказался ноль. В нашем примере к первой строке матрицы 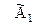нужно прибавить вторую строку матрицы 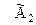, умноженную на (-2), получим: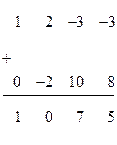

Теперь матрица 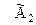будет иметь вид:

.

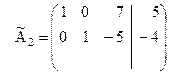4. Чтобы найти третью строку матрицы 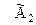, к третьей строке матрицы 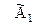прибавим новую вторую строку из матрицы 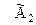, предварительно умножив ее на такое число, чтобы во

втором столбце оказался ноль. В нашем примере к третьей строке матрицы 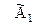нужно прибавить вторую строку матрицы 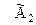, умноженную на (+2), получим: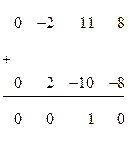

Теперь матрица 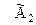будет иметь вид:

.

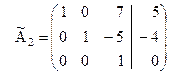Если матрицу 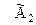рассматривать, как систему уравнений, то увидим, что в результате элементарных преобразований получили систему равносильную исходной, причем неизвестная

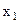исключена из всех уравнений кроме первого а 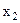из всех уравнений кроме второго.

Третий шаг решения (III шаг) состоит в том, что неизвестная 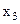исключается из всех уравнений кроме третьего, а в третье должна входить с коэффициентом единица.

.

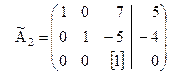Следовательно, на третьем шаге третья строка и третий столбец будут разрешающими, а разрешающий элемент оказался равным единице. Поэтому третий шаг сразу можно начать с исключения 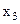из всех уравнений кроме разрешающего. В нашем примере нужно к первой строке прибавить разрешающую, умноженную на (-7), а ко второй прибавить разрешающую строку, взятую с коэффициентом (5). В результате получим новую матрицу :

.

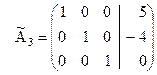Если заменить эту матрицу соответствующей ей системой уравнений, то получим ответ:

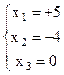
Обобщив все проведенные в примере вычисления, можно сформулировать в общем виде алгоритм любого (к - го) шага.

Алгоритм к – го шага.

(1) Выбираем к – ую разрешающую строку среди тех строк, которые еще не были разрешающими и у которых на к – ом месте стоит элемент отличный от нуля. При этом к – ый столбец будет разрешающим столбцом, а элемент стоящий на их пересечении – разрешающим элементом.

(2) Разрешающую строку делим на разрешающий элемент и записываем на к – ое место в новой матрице.

(3) Ко всем остальным строкам матрицы, полученной на предыдущем шаге, прибавляем строку, полученную в (2) и взятую с таким коэффициентом, чтобы в к – ом столбце новой матрицы все элементы кроме к – го оказались нулями.

Примечания

1. Если в процессе вычислений появятся несколько одинаковых строк, то все кроме одной нужно отбросить.

2. Если в процессе решения появится нулевая строка, то ее нужно отбросить.

3. Все элементы любой строки можно умножать или делить на число отличное от нуля.

4. Если в строке только последний элемент отличен от нуля, то система противоречива

и решений не имеет.

5. Если на последнем шаге оказывается, что количество неизвестных больше, чем

количество уравнений, то система имеет бесчисленное множество решений.

Пример Система трёх линейных уравнений с тремя неизвестными х₁, х₂, х₃

задана расширенной матрицей .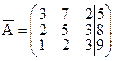

Требуется:

1) записать систему в канонической форме (в виде системы уравнений),

2) решить эту систему по формулам Крамера, причём определители вычислять,

используя их свойства.

Решение

1) Каноническая форма системы: .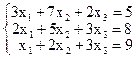

2) Вычисляем определитель системы :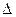

.

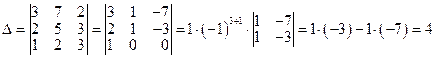Алгоритм: Первый столбец умножим на (-2) и прибавим ко второму столбцу, а к третьему столбцу прибавим первый, умноженный на (-3). При этом все элементы последней строки кроме первого окажутся равными нулю.

Разложим определитель по элементам третьей строки.

Определитель системы 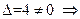система имеет единственное решение, которое можно найти по формулам Крамера: .

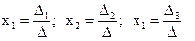3) Из определителя системы 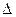составим определитель 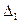, заменив в нём

первый столбец столбцом свободных членов и вычислим его:

.

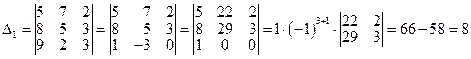Алгоритм: Вторую строку умножим на (-1) и прибавим к третьей строке.

Первый столбец умножим на (+3) и прибавим ко второму столбцу.

Разложим определитель по элементам третьей строки.

4) Из определителя системы 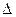составим определитель 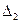, заменив в нём

второй столбец столбцом свободных членов и вычислим его:

.

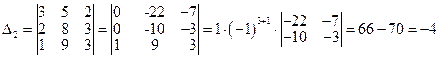5) Из определителя системы 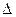составим определитель 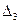, заменив в нём

третий столбец столбцом свободных членов и вычислим его:

.

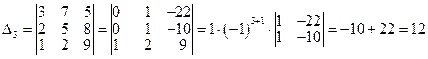6) Подставляем найденные значения в формулы Крамера, тогда получим:

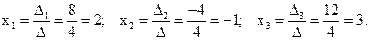
7) Чтобы убедиться в правильности решения, подставим найденные

значения неизвестных в исходную систему: .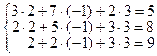

8) Ответ: .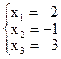

Векторная алгебра.

Пример. Даны вершины пирамиды ,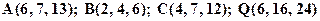

причём точки A, B, C - вершины её основания.

Средствами векторной алгебры найти:

1) векторы с началом в точке В и концом в остальных вершинах пирамиды;

2) длину и направляющие косинусы вектора ;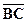

3) скалярное произведение векторов 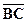и ;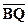

4) угол 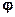между рёбрам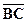и и ;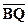

5) векторное произведение векторов 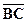и ;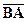

6) площадь основания пирамиды;

7) смешанное произведение векторов с началом в точке В

и концом в остальных вершинах пирамиды;

8) объём пирамиды.

Решение

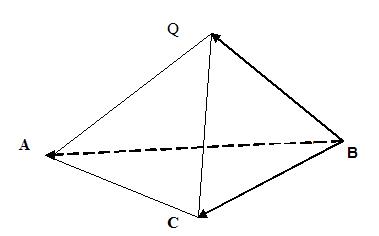
Рис. 1.

1) В координатной форме вектор можно задать следующим образом:

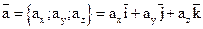, где 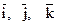- орты осей координат.

Чтобы найти координаты вектора нужно от координат конца вычесть координаты

начала: .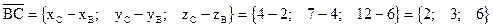

.

.

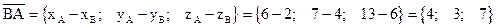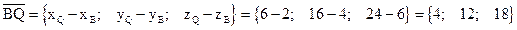2) Длина вектора равна корню квадратному из суммы квадратов всех его координат:

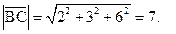
Направляющие косинусы вектора это косинусы углов между вектором и осями координат.

Чтобы их найти нужно соответствующую координату вектора разделить на его длину.

Следовательно, направляющие косинусы вектора :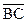

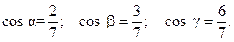
Чтобы проверить правильность этих вычислений , найдём сумму квадратов направляющих косинусов, она должна быть равна единице: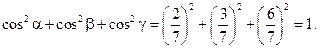

3) Скалярное произведение двух векторов можно вычислить как сумму произведений одноимённых координат, поэтому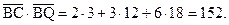

4) Косинус угла между векторами равен их скалярному произведению, делённому на произведение их длин: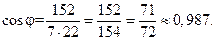

5) Если векторы заданы своими координатами: 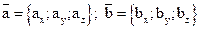, а ортами координатных осей являются векторы 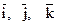, то их векторное произведение это вектор 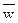, который можно найти разложив по первой строке определитель третьего порядка:

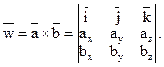
Тогда .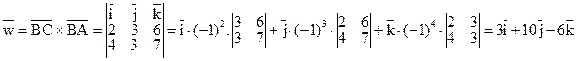

6) Площадь 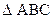найдём используя геометрический смысл векторного произведения векторов: .

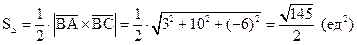7) Смешанное произведение трёх векторов, заданных в координатной форме,

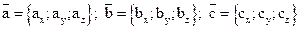, равно определителю третьего порядка:

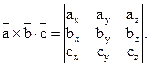
Тогда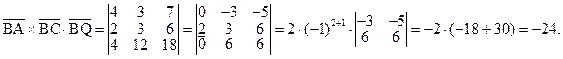

8) Объём пирамиды найдём, используя геометрический смысл смешанного произведения векторов: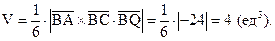

Прямая линия на плоскости

Пример. Треугольник АВС задан своими вершинами: 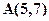; ; 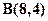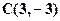(рис. 2).

Найти: 1) уравнение стороны ВС (в отрезках на осях),

2) уравнение стороны ВА (в общем виде),

3) угол между сторонами ВСи ВА,

4) уравнение медианы ВМ(с угловым коэффициентом),

5) уравнение высоты АК (с угловым коэффициентом),

6) уравнение прямой L, проходящей через точку С || ВА,

7) длину высоты h, проведённой из вершины С.

Решение

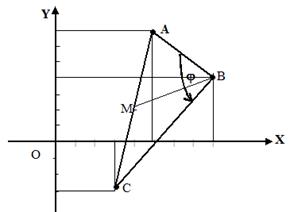
Рис. 2.

1) На искомой прямой известны две точки, поэтому воспользуемся уравнением прямой ВС, проходящей через две точки: 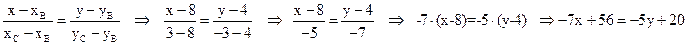(ВС): 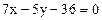- общее уравнение прямой ВС.

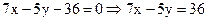. Уравнение прямой в отрезках на осях 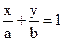получим, поделив уравнение на 36 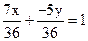и переведя 7 и -5 в знаменатель

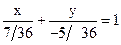- уравнение прямой ВС в отрезках на осях.

2) Уравнение прямой ВА находим тем же способом.

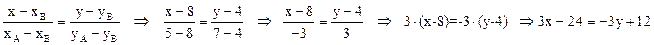(ВА): 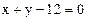- уравнение прямой ВА в общем виде.

3) Угол 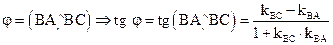, где 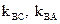- угловые коэффициенты соответствующих прямых. Поэтому нужно найти их угловые коффициенты.

(ВС):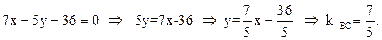

(ВА):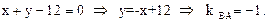

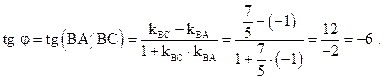
Тангенс угла отрицательный, следовательно, угол между сторонами ВА и ВС – тупой, поэтому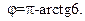

4) Медиана ВМ делит сторону АС на равные части: .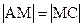

Найдём координаты точки М: .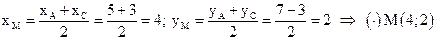

(ВМ): .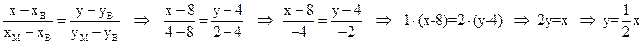

5) .

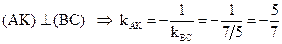Уравнение прямой АК найдём как уравнение прямой, проходящей через данную точку А в данном направлении: (АК):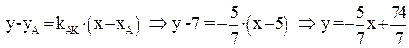

6) L || ВА , следовательно .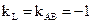

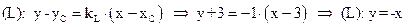7) Длину высоты h, опущенной из вершины С, можно найти как расстояние от точки С до противоположной стороны АВ: