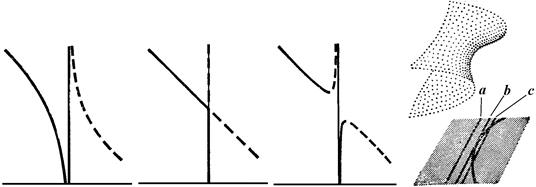
Геометрия прощелкивания арки
Чувствительность к несовершенству. Если один стержень в сложной конструкции начинает менять свою форму – тем более если несколько стержней сделают это одновременно, – это может вызвать более радикальное поведение системы, чем то, которое изучалось ранее. Но поведение арки из предыдущего параграфа уже является внезапным и радикальным.
Система, для которой симметрия задачи является совершенной, даст бифуркацию энергии, приводимой к виду
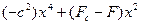 ,
,
где Fc – критическая нагрузка, а с – константа.
На рисунке а изображены соответствующие равновесные пути, жирные для минимумов (устойчивые равновесия) и штриховые – для неустойчивых равновесий. Отличие этого предыдущего рисунка состоит в том, что здесь предполагается существование структурно устойчивого решения. Эта картинка представляет собой обычное центральное сечение двойственной сборки. Она точно так же неустойчива, если рассмотреть для малого 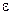 функцию
функцию
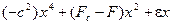 ,
,
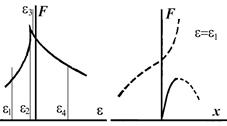
то рис. а заменится на рис. б, где наибольшее значение F, для которого существуют устойчивые равновесия, существенно ниже. Точнее говоря, нагрузка потери устойчивости как функция от 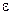 задается бифуркационным множеством катастрофы двойственной сборки (рис. в). Устойчивое равновесие локально существует лишь для (F,
задается бифуркационным множеством катастрофы двойственной сборки (рис. в). Устойчивое равновесие локально существует лишь для (F, 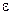 ) внутри острия сборки. Обратите внимание на быстрое падение от значения Fc с ростом |
) внутри острия сборки. Обратите внимание на быстрое падение от значения Fc с ростом | 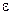 |.
|.
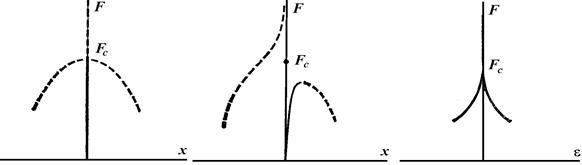
А б в
Рисунок 1.46 - Каноническая диаграмма: а, б – кривые нагрузка – перемещение; в – кривую чувствительности к несовершенствам
Именно с этого начался строгий анализ чувствительности к несовершенству. Значительное внимание стало уделяться показателям чувствительности к несовершенству. Поскольку из рис. в ясно, что нагрузка потери устойчивости не является гладкой функцией параметра несовершенства 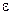 , нужно исследовать ее особенности. В нашем случае особенность подчиняется закону (нагрузка потери устойчивости)
, нужно исследовать ее особенности. В нашем случае особенность подчиняется закону (нагрузка потери устойчивости) 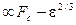 в исходных координатах (где символ
в исходных координатах (где символ 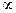 имеет свое обычное физическое значение предельного показателя). Разумеется, доказать через четверть века, что в подходящих координатах ,,
имеет свое обычное физическое значение предельного показателя). Разумеется, доказать через четверть века, что в подходящих координатах ,, 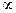 " можно заменить на „=", не бог весть какой триумф теории катастроф в инженерном деле! Особенно если учесть, что тем временем отчасти эвристическое использование разложений Тейлора получило мощное развитие. Для рассматриваемого случая всё имеющее практическую важность было сказано прежде, чем на сцену вышла теория катастроф.
" можно заменить на „=", не бог весть какой триумф теории катастроф в инженерном деле! Особенно если учесть, что тем временем отчасти эвристическое использование разложений Тейлора получило мощное развитие. Для рассматриваемого случая всё имеющее практическую важность было сказано прежде, чем на сцену вышла теория катастроф.
В частности, в отличие от подхода, сосредоточенного исключительно на путях и их ветвлениях, подход с многообразием катастрофы был введен для случая двух измерений (равновесная поверхность) Сьюэллом. Он на примере установил решающее для топологического анализа, основанного на стратификации, обстоятельство, что кривая складок оказывается гладкой в многообразии катастрофы, а особенность типа острия имеет место для ее проекции в пространство параметров деформации.
Теория катастроф может быть применена и к особенностям, более высоким, чем сборка. Надежды, возлагаемые на эту теорию, связаны с тем, что она позволяет управиться с этими высшими особенностями, и с ее критериями для достаточного числа параметров деформации. При этом наибольшее значение приобретают вычислительные аспекты теории.
В инженерном деле, где количественная информация часто бывает легкодоступной, это может быть использовано для распознавания катастрофы. Никто никогда не предлагал решать инженерные задачи подгонкой известных данных под семь элементарных катастроф из списка Тома. Во-первых, потому, что это было бы невозможно, а во-вторых, потому, что у нас в распоряжении есть гораздо более мощные вычислительные средства.
Область, в которой методы аппроксимации Тейлора, практикуемые инженерами и систематизированные теорией катастроф, дают хорошее согласие с практикой уже в исходных координатах, часто оказывается достаточно широкой. Рисунок 1.47 получен при изучении другой двойственной сборки (подпертая консоль), в котором точное бифуркационное множество оказалось необычайно легко отыскать в явном виде.
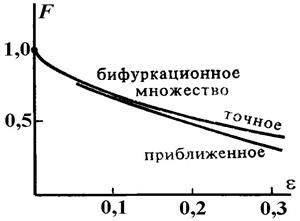
Рисунок 1.47 - Сравнение эксперимента и теории
Бифуркации сборки и двойственной сборки часто дают одинаково хорошее согласие с экспериментом.
Отметим, что степенной закон с показателем 2/3, предсказанный геометрией, выполняется лучше, чем симметрия. Неизбежные экспериментальные погрешности сдвигают немного острие в плоскости ( 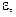 F), но это может быть скомпенсировано небольшой заменой координат.
F), но это может быть скомпенсировано небольшой заменой координат.
Приведем также следующую численную характеристику влияния несовершенств: асимметрия, эквивалентная перемещению груза примерно на L/500 в сторону, понижает нагрузку, при которой происходит прощелкивание, почти на 6%.
Но иногда локальное так и означает локальное – не более того. Например, рис., б показывает, что двойственная сборка может иметь лишь локальное влияние. Вторичные бифуркации, представленные двумя близкими стандартными сборками, скрадывают ее, если смотреть в более крупном масштабе. Как можно видеть из приведенной на рисунке диаграммы ветвления для совершенной (G= 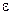 =0) системы, указанные на рисунке скачки, происходящие при возрастании F, будут совсем незначительными вблизи точки бабочки.
=0) системы, указанные на рисунке скачки, происходящие при возрастании F, будут совсем незначительными вблизи точки бабочки.
Найти эти вторичные складки удалось, проследив их от первичной точки бабочки при изменении параметра 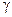 , а не с помощью специального исследования вторичных бифуркаций, которое обычно сложнее. Когда вторичные бифуркации имеют организующий центр, как здесь, лучше варьировать несколько дополнительных параметров, чтобы им воспользоваться, даже в случае, если на самом деле их значения фиксированы для данной системы.
, а не с помощью специального исследования вторичных бифуркаций, которое обычно сложнее. Когда вторичные бифуркации имеют организующий центр, как здесь, лучше варьировать несколько дополнительных параметров, чтобы им воспользоваться, даже в случае, если на самом деле их значения фиксированы для данной системы.
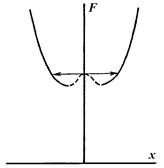
Рисунок 1.48 - Диаграмма ветвления для совершенной системы
  а б в а б в | 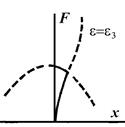 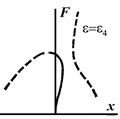 г д г д |
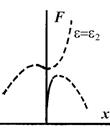
Рисунок 1.49 - Канонически диаграммы при плавном изменении 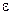 слева на право
слева на право
Хотя переход от рисунка а к б важен, он ни в коем случае не является единственно возможным возмущением для рисунка 1, а. В частности, произвольно малое несовершенство в системе может отклонить вершину острия в плоскости ( 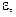 F),как показано на рис. 2, а. Например, легкий наклон установки даст такой эффект. Геометрия сборки сохранится, благодаря структурной устойчивости, но характер ветвления равновесных путей при различных фиксированных значениях
F),как показано на рис. 2, а. Например, легкий наклон установки даст такой эффект. Геометрия сборки сохранится, благодаря структурной устойчивости, но характер ветвления равновесных путей при различных фиксированных значениях 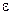 радикально изменится. Последовательность рисунок 4.49 б – д отвечает изменению
радикально изменится. Последовательность рисунок 4.49 б – д отвечает изменению 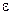 слева направо на рис. а.
слева направо на рис. а.
Если проводить жесткое различие между параметрами несовершенства, рассматриваемыми как фиксированные для данной физической конструкции, и параметрами нагрузки, которые варьируются, то преобразования, которые перемешивают эти переменные, запрещаются.
Однако, лишь располагая такими преобразованиями, можно считать геометрию рис. 1 эквивалентной геометрии рис. 2. Поэтому наклон становится параметром несовершенства нового типа, действие которого не устраняется в этом новом классе допустимых преобразований.
Это особенно наглядно показывает следующем рисунке, из которого видно, что при малом наклоне нагрузка, при которой впервые происходит прощелкивание (жирная кривая), становится разрывной функцией от 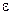 , а не просто функцией, имеющей особенности.
, а не просто функцией, имеющей особенности.
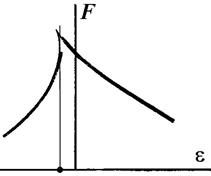
Рисунок 1.50 - Уточненная кривая чувствительности к несовершенству
Количественно эта чувствительность к малым наклонам не так резка, как чувствительность к малым 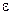 . Для канонической двойственной сборки несложно подсчитать, что максимум нагрузки падает квадратично с ростом наклона, а не с каким-либо дробным показателем.
. Для канонической двойственной сборки несложно подсчитать, что максимум нагрузки падает квадратично с ростом наклона, а не с каким-либо дробным показателем.
Однако такая мягкость не является универсальной для несовершенств. Возьмем, например, катастрофу складки. Если складка пересекается обычно (трансверсально) при изменении нагрузки, взятой в качестве управляющего параметра, результат получится устойчивый и будет гладко отвечать на любые несовершенства. Но если энергия приводится для совершенной системы к виду
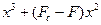 ,
,
результаты будут совсем другими. Это семейство, дополненное одним членом:
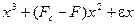
приводится к стандартной складке (рисунке 1.51 d).
Здесь совершенно необоснованны преобразования, которые приходится при этом привлекать, поскольку нельзя менять несовершенство по ходу изменения F, с тем, чтобы превратить нагрузку в немой параметр. Это ограничение приводит к тому, что в то время как отрицательные значения 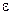 дают очень слабый эффект (рис. а), положительные приводят к прощелкиванию (рис. , с), и притом с худшим понижением максимальной нагрузки, чем в задаче для арки, рассмотренной выше. Из рис. d ясно, что падение происходит по закону
дают очень слабый эффект (рис. а), положительные приводят к прощелкиванию (рис. , с), и притом с худшим понижением максимальной нагрузки, чем в задаче для арки, рассмотренной выше. Из рис. d ясно, что падение происходит по закону 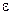 1/2, а не
1/2, а не 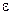 2/3.
2/3.