Предмет теоретической механики

Теоретическая механика - это раздел механики, изучающий движение абсолютно твердого тела.

Абсолютно твердым или недеформируемым называется тело, у которого расстояния между двумя любыми точками остаются неизменными.

Частным случаем твердого тела является материальная точка – это тело, размерами которого в условиях конкретной задачи можно пренебречь.

В зависимости от особенностей механического движения теоретическая механика (ТМ) делится на статику, кинематику и динамику.

Статика рассматривает частный случай механического движения, когда оно не зависит от времени – речь идет о рассмотрении равновесия твердого тела (ТТ), загруженного системой сил и находящегося в состоянии покоя.

Кинематика рассматривает внешнюю сторону механического движения независимо от причин, вызвавших его. Это не что иное, как геометрия в четырехмерном пространстве, где время играет роль четвертого измерения.

Если известно положение движущейся точки в каждый момент времени, то кинематика позволяет построить ее траекторию и определить такие кинематические параметры, как скорость или ускорение.

Динамика исследует общий случай механического движения ТТ с учетом причин, вызвавших его.

Нетрудно догадаться, что при изучении ТМ нас, прежде всего, будет интересовать статика.

Высокая степень абстракции модели абсолютно твердого тела позволяет применять в ТМ, как и в математике, аксиоматико-дедуктивный метод исследования. Это означает, что ТМ (и в частности статика) подобно геометрии построена на системе аксиом, сформулированных Ньютоном, которые играют в механике ту же роль, что и аксиомы Евклида в геометрии.

Таким образом, изучение ТМ помимо решения основной задачи способствует формированию рационального логического мышления.

Остается ответить на вопрос, зачем нужно изучать теоретическую механику архитектору? В значительной мере ответ на этот вопрос уже дан в предисловии к настоящему пособию. В дополнение к этому отметим, что задачей архитектурного проектирования является организация окружающего пространства с учетом:

- функциональных требований,

- законов физики и механики,

- опыта проектирования,

- эстетических концепций,

- экономичности

и ряда других требований.

Знание основных законов строительной механики является необходимым условием проектирования реальных и рациональных сооружений. Их учет позволяет уже на начальной стадии разработки проекта исключить заведомо нереализуемые варианты.

В прошлом незнание этих законов архитекторы могли компенсировать только учетом опыта проектирования и своей интуицией, при этом принятие новых конструктивных решений сопровождалось повышенным риском.

Сегодня такой метод проб и ошибок был бы слишком дорогим и неоправданным, поскольку расширение наших знаний в области строительной механики и появление автоматизированных систем проектирования позволяют архитектору в полной мере реализовать свой творческий потенциал.

Основные понятия статики

Прежде, чем перейти к рассмотрению аксиом статики, поясним основные понятия, с которыми мы там встретимся.

Статика – это раздел теоретической механики, изучающий условия равновесия систем сил и методы замены этих систем эквивалентными.

Сила – векторная величина, характеризующая воздействие на тело другого материального объекта. Сила определяется тремя факторами:

- точкой приложения,

- линией действия или направлением,

- модулем или величиной.

Системой называется совокупность сил, приложенных к одному твердому телу.

Эквивалентными называются системы сил, оказывающие на тело одинаковое воздействие.

Условие эквивалентности систем сил будем записывать в виде:

(P₁, P₂, ..., P_m) ~ (F₁, F₂, …, F_n).

Равнодействующей называется сила, эквивалентная системе сил:

R ~ (R) ~ (P₁, P₂, …, P_n).

Уравновешенной называется система сил, равнодействующая которой существует и равна нулю:

(P₁, P₂, ... , P_n) ~ 0.

Уравновешивающей называется сила, равная и противоположная по направлению равнодействующей.

Все тела в механике делятся на свободные и несвободные.

Свободное тело может перемещаться в пространстве в любом направлении.

Несвободным называется тело, перемещения которого ограничены наложенными на него связями, то есть другими телами, ограничивающими свободу перемещений первого тела.

Все силы в механике делятся на активные и реакции связей или реактивные.

Последние могут появляться только в ответ на действие активных сил.

Отметим, что реакция связи направлена в сторону, противоположную тому направлению, куда тело не может перемещаться вследствие наложенной на него связи.

ПРИМЕЧАНИЯ:

1. В соответствии с приведенным определением сила является точечным вектором в отличие от векторов в математике, где векторы являются свободными.

2. Как обычно, здесь и в дальнейшем для обозначения векторных величин мы будем применять полужирный шрифт.

3. Понятия «линия действия» и «направление» близки, но не тождественны. Очевидно, что по линии действия можно определить направление с точностью до противоположного. Аналогично связаны понятия «модуль» и «величина» для вектора.

Аксиомы статики

Система аксиом статики, о которой мы уже упоминали, была сформулирована И.Ньютоном в 1687 г. в его работе «Математические основы натуральной философии». Часть этих аксиом известна из школьного курса физики как законы Ньютона, хотя первый из них – закон инерции был сформулирован еще Г.Галилеем.

1. Аксиома инерции. Под действием уравновешенной системы сил тело движется прямолинейно и равномерно или находится в состоянии покоя.

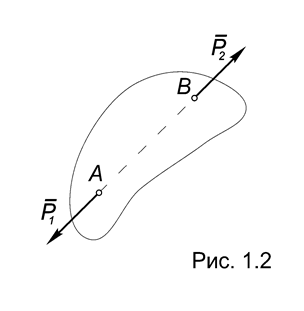
2.Аксиома равновесия системы двух сил. Система двух сил уравновешена в том и только в том случае, если эти силы:

- действуют по одной прямой, соединяющей точки их приложения;

- равны по модулю;

- направлены в противоположные стороны (Рис.1.2).

Отметим, в частности, что из условия: (Р₁ , Р₂) ~ 0 следует, что P₁ = - P₂.

3.Аксиома присоединения или исключения уравновешенной системы сил. Действие системы сил на тело не изменится, если к ней присоединить (исключить из нее) уравновешенную систему сил.

Следствием этой аксиомы является следующая

Теорема 1.1. Действие силы на ТТ не изменится, если эту силу перенести вдоль линии действия в любую точку этого тела.

Формулировка теоремы означает, что сила Р, приложенная в точке А твердого тела, эквивалентна силе Р¢ , приложенной в точке В того же тела и лежащей на линии действия силы Р. При этом вектор Р равен вектору Р¢ : Р = Р¢ (Рис.1.3а, в).

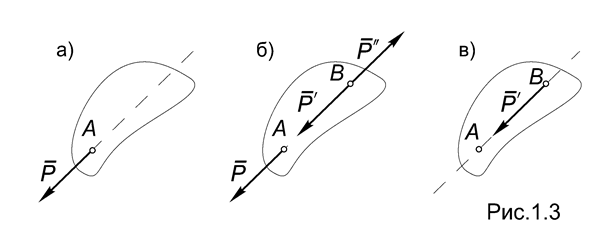
Для доказательства присоединим к системе, состоящей из единственной силы Р , уравновешенную систему сил, приложенных в точке В : (Р¢, Р¢¢ ) ~ 0, выбрав Р¢ = Р = - Р¢¢ (Рис.1.3б).

Тогда в силу аксиом 2 и 3:

(Р ) ~ (Р,(Р¢, Р¢¢ )) ~ ((Р, Р¢¢ ), Р¢ ) ~ (Р¢ ),

поскольку силы (Р, Р¢¢ ) также образуют уравновешенную систему. Теорема доказана.

4.Аксиома параллелограмма. Равнодействующая двух пересекающихся сил приложена в точке пересечения их линий действия и изображается диагональю параллелограмма, построенного на этих силах как на сторонах.

Отметим, что математически рассмотренная процедура определения равнодействующей соответствует нахождению суммы векторов (Рис.1.4):

(P₁, P₂) ~ R ð R = P₁ + P₂ .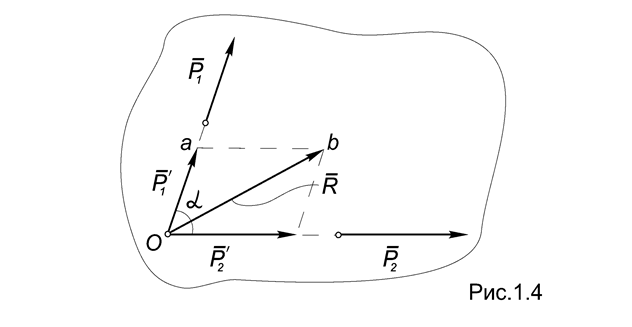

Для определения модуля равнодействующей возведем последнее выражение в квадрат:

½R½²=R² = (P₁ + P₂ )² = P₁² + P₂² + 2 (P₁ × P₂) = P₁² + P₂² + 2 P₁ P₂ cos (P₁, P₂),

откуда получим искомое выражение:

________________

R = Ö P₁² + P₂² + 2 P₁ P₂ cos a ,

где a - угол между векторами P₁ и P_2.

Построение параллелограмма можно, очевидно, заменить построением силового треугольника Oab.

5.Аксиома действия и противодействия. Два тела взаимодействуют с силамиP₁ и P₂, равными по величине и противоположными по направлению:

P₁ = - P₂.

Отметим, что эти силы в отличие от сил, о которых идет речь в аксиоме 2, системы не образуют, поскольку приложены к разным телам.

6.Аксиома отвердевания. Равновесие деформируемого тела не нарушится, если его считать абсолютно твердым.

Эта аксиома позволяет рассматривать равновесие не только абсолютно твердых, но также деформируемых тел и даже жидкости. Например – в гидростатике.

7.Аксиома освобождаемости от связей. Несвободное тело можно считать свободным, если вместе с активными силами приложить к нему реакции отброшенных связей.

Отметим, что во всех предыдущих аксиомах рассматривались свободные тела. Соответственно для свободных тел впоследствии будут получены условия равновесия и теоремы статики. В то же время все окружающие нас строительные конструкции и сооружения представляют собой примеры тел несвободных. Отсюда понятна значимость последней аксиомы, которая позволяет от несвободных тел переходить к свободным, а также необходимость умения определять реакции этих связей.

ПРИМЕЧАНИЯ:

1. Аксиома 1 справедлива только для частного случая ТТ – материальной точки.

2. На основании следствия из аксиомы 3 сила в ТМ является не точечным, а скользящим вектором, поэтому на практике точка ТТ, к которой приложена сила, может совпадать как с началом, так и с концом этого вектора.

3. С помощью аксиомы 4 можно выполнить и обратную операцию: разложить силу на две составляющие по двум заранее выбранным направлениям.

4. Здесь и далее, если это не вызывает недоразумения, мы применяем обычное начертание шрифта для обозначения как модуля вектора силы, так и его величины: P =±½P½.

Простейшие типы связей

1. Идеально гладкая поверхность. Рассмотрим тело, которое может перемещаться без трения по гладкой горизонтальной поверхности (Рис.1.5а). Пусть в качестве активной силы выступает сила веса - Р, приложенная в его центре тяжести. Реакция связи N представлена силой, распределенной по плоскости нижней грани этого тела, и ее можно считать приложенной в центре этой грани.

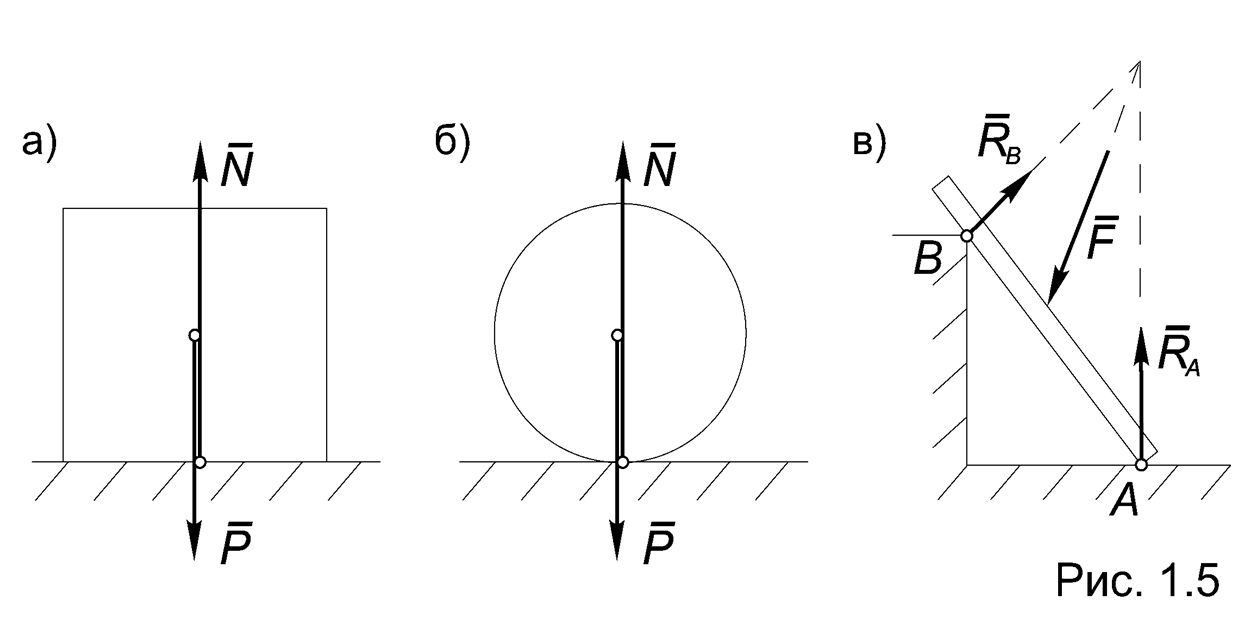
Принципиально картина не меняется, если поверхность тела или связи будет гладкой, но криволинейной (Рис.1.5б).

Пусть тело в виде бруса с гладкой поверхностью опирается в точке А на идеально гладкую поверхность, а в точке В - на уступ (Рис.1.5в).

Нетрудно догадаться, что тело не сможет находиться в равновесии, если в качестве активной силы выступает его собственный вес, однако равновесие возможно, если к этому брусу приложить некоторую другую внешнюю силу F. При этом, как будет показано в следующей главе, равновесие возможно только в том случае, если линия действия этой силы проходит через точку пересечения линий действия реакций R_A и R_B .

Итак, по поводу этого типа связи можно сделать следующий вывод: реакция идеально гладкой поверхности приложена в точке касания и направлена по нормали к поверхности тела или связи.

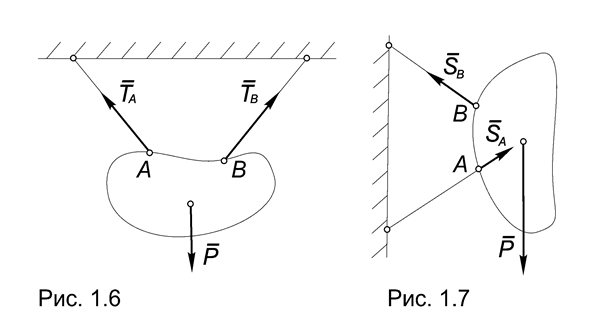
2. Гибкая невесомая и нерастяжимая нить. Рассмотрим тело, которое подвешено на двух таких нитях и находится в равновесии под действием собственного веса и реакций нитей, прикрепленных к телу в точках А и В (Рис.1.6).

Реакция связи равна силе натяжения нити, она направлена вдоль нити и от тела, которое эта нить удерживает.

3. Жесткий невесомый прямолинейный стержень. Реакция направлена вдоль стержня, который, в отличие от нити, может воспринимать как растягивающие (S_B), так и сжимающие (S_A) усилия (Рис.1.7).

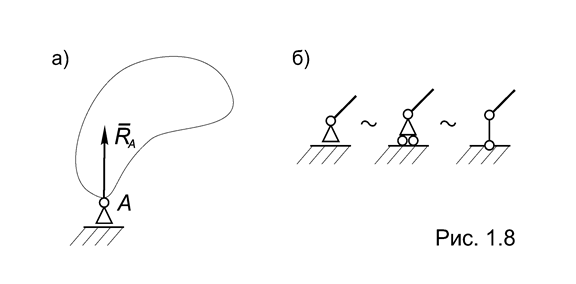
4. Подвижная опора. Допускает перемещение закрепленным таким образом точки тела только вдоль опорной плоскости (Рис.1.8а).

Реакция направлена перпендикулярно заштрихованной опорной площадке.

В учебной литературе этот вид связи также называют подвижным цилиндрическим шарниром.

Помимо стандартного обозначения, предусмотренного ГОСТом, на схемах эту связь изображают так, как показано на рис. 1.8б.

Отметим, что четыре рассмотренные связи имеют одну общую особенность: соответствующие им реакции известны по направлению и неизвестны по величине. То есть с точки зрения алгебры каждая из этих реакций соответствует только одному неизвестному.

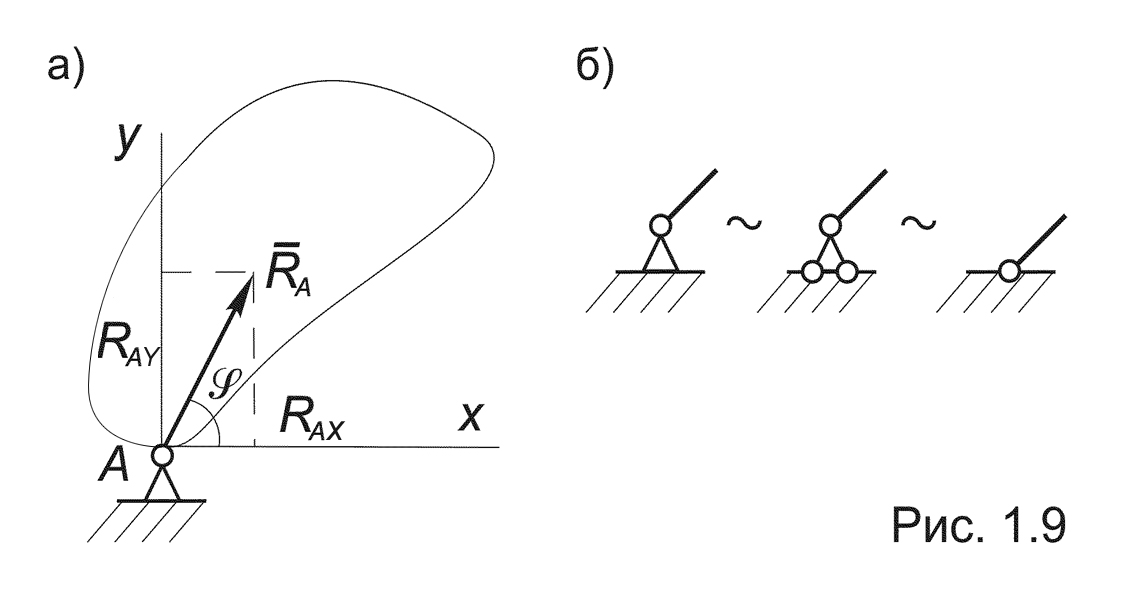
5. Неподвижная опора. Препятствует перемещению закрепленной таким образом точки тела в горизонтальном и вертикальном направлениях. Это означает, что в общем случае реакция R_Aтакой связи неизвестна по величине и по направлению. В качестве неизвестных при ее определении можно выбрать модуль реакции -½R_A½и угол j, который она образует с осью Ox , либо проекции вектора R_A на оси координат: R_AX , R_AY (Рис.1.9а).

Эта связь допускает поворот тела вокруг рассматриваемой точки, поэтому в учебной литературе эту связь также называют неподвижным цилиндрическим шарниром.

Помимо стандартного обозначения, предусмотренного ГОСТом, на схемах она изображается так, как показано на рис. 1.9б.

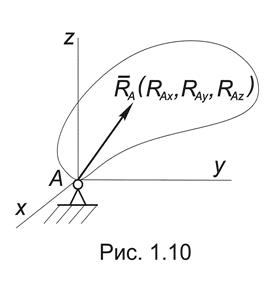
6. Сферический шарнир. В отличие от цилиндрического шарнира не допускает перемещения закрепленной таким образом точки тела в трех взаимно перпендикулярных направлениях. В качестве неизвестных при ее определении выбирают проекции этой реакции на оси координат: R_AX , R_AY , R_AZ (Рис.1.10).

Рассмотренными в этом параграфе шестью типами связей мы и ограничимся. Другие связи будут рассмотрены по мере необходимости.

ПРИМЕЧАНИЯ:

1. В соответствии с аксиомой 7 на схемах нужно изображать одно из двух: либо связи, либо реакции отброшенных связей. На практике реакции связей нередко изображают одновременно со связями.

2. Связи, как и другие понятия, встречающиеся в аксиомах, являются абстракциями, весьма условно отражающими свойства реальных объектов. Например, рассмотренная выше гибкая невесомая нить может быть моделью подвесных и вантовых систем, у которых масса погонного метра троса составляет десятки и сотни килограммов. Однако усилия, возникающие в таких тросах, во столько раз больше их собственного веса, что при расчете последним можно пренебречь, считая их невесомыми.