Пример 4.6.2-5. Написать процедуру-Sub, вычисляющую сумму всех чисел Фибоначчи, которые не превосходят заданного натурального числа m, и определить количество таких чисел.
Числа Фибоначчи (Fi) определяются по формулам
F0 = F1 = 1; Fi = Fi –1 + Fi –2, при i = 2, 3,...,…
т.е. каждое очередное число равно сумме двух предыдущих.
Подобная задача была решена при рассмотрении регулярных циклических структур (пример 5.2-4). Однако здесь число слагаемых (членов последовательности) заранее неизвестно, поэтому организуем итеративный цикл с предусловием. Обозначим это число слагаемых k. В данном примере до начала цикла задаются значения трех чисел Фибоначчи F0, F1, и F2 = F0 + F1 = 2 и их сумма S = F0 + F1 + F2 = 4. В цикле переопределяем значение переменных F0 и F1, выводим очередное (предыдущее) число Фибоначчи, вычисляем следующее число и добавляем его в сумму. Когда текущее число Фибоначчи превосходит заданное число m (F2 ≤ m – False), то происходит выход из цикла. Так как это число Фибоначчи уже добавлено в сумму, то после выхода из цикла его необходимо вычесть из нее (S = S - F2). Таким образом, в окончательном значении суммы будут учтены только те числа Фибоначчи, которые еще не превосходят m.
| Sub P6212(ByVal m As Integer, _ ByRef S As Long, ByRef k As Integer) Dim F, F1, F2 As Integer F0 = 1 : F1 = 1 : F2 = 2 S = F0 + F1 + F2 : k = 3 Do While F2 <= m F0 = F1 : F1 = F2 vivodIntLs12(F1, ListBox1) F2 = F0 + F1 S = S + F2 K = k + 1 Loop S = S – F2 k = k - 1 End Sub |
Рис. 4.6.2-12. Схема алгоритма и программный код процедуры Pr6212(),
которая вычисляет сумму чисел Фибоначчи,
не превосходящих заданного натурального числаm
Примера 4.6.2-5
Схема алгоритма и код процедуры-Sub приведены на рис. 4.6.2-12.
Процедура-Sub Pr6212() может быть вызвана из любой другой процедуры или из модуля формы, например, как показано на рис. 4.6.2-13.
| Dim SS As Long Dim mm, kk As Integer mm=vvodInt9("Введите значение mm= ", TextBox1) Pr6212(mm, SS, kk) vivodFxn14(SS, kk, TextBox2) |
Рис. 4.6.2-13. Пример обращения к процедуре Pr6212()
Примера 4.6.2-5
Пример 4.6.2-6. Написать процедуру-Function, которая вычисляет с точностью e=0.001 сумму членов ряда
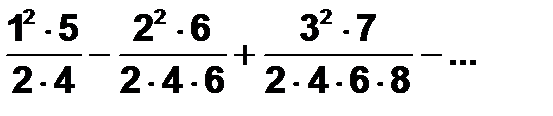 .
.
Задана знакопеременная убывающая последовательность, поэтому для вычисления суммы ряда с точностью e будем вычислять и суммировать члены последовательности до тех пор, пока очередной член ряда не станет меньше заданной точности по модулю.
Заданный ряд вычислять через рекуррентную формулу нецелесообразно, так как это, во-первых, трудно, а во-вторых, скорее всего, невозможно вывести общую формулу n-гол члена ряда. Поэтому можно воспользоваться следующим универсальным приемом вычисления подобных рядов. Каждый член последовательности можно представить, как 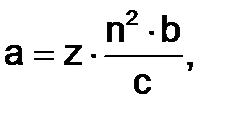 где z– множитель, равный 1 или -1 (знак члена ряда); n – первый сомножитель в числителе каждого слагаемого (в данном случае совпадает с номером члена ряда); b – второй сомножитель в числителе; с – знаменатель каждого слагаемого.
где z– множитель, равный 1 или -1 (знак члена ряда); n – первый сомножитель в числителе каждого слагаемого (в данном случае совпадает с номером члена ряда); b – второй сомножитель в числителе; с – знаменатель каждого слагаемого.
В свою очередь, знаменатель члена ряда представляет собой произведение нескольких сомножителей, причем с увеличением номера члена ряда увеличивается и количество сомножителей в знаменателе. Таким образом, знаменатель можно представить, как с = с * d, где d – сомножитель, добавленный к значению знаменателя предыдущего члена ряда.
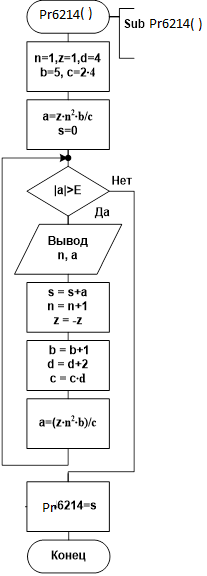
Схема алгоритма и код процедуры-функции приведены на
рис. 4.6.2-14.
 | Function Pr6214(ByVal E As Double) _ As Double Dim a, s As Double Dim n, z, b, c, d As Integer n = 1 z = 1 b = 5 c = 2 * 4 d = 4 a = z * n^ 2 * b / c s = 0 Do While Abs(a) > E vivodIntLs12(n, ListBox1) vivodDblLs13(a, ListBox2) s = s + a n = n + 1 z = -z b = b + 1 d = d + 2 c = c * d a = z * n^ 2 * b / c Loop Return s End Function |
Рис. 4.6.2-14. Схема алгоритма и программный код процедуры Pr6214(),
которая вычисляет с точностью e=0.001 сумму членов заданного ряда
Примера 4.6.2-6
Процедура-Function Pr6214( ) может быть вызвана из любой другой процедуры или из модуля формы, например, как показано на рис. 4.6.2-15.
| Dim EE, SS As Double EE =vvodDbl1(TextBox1) SS = Pr6214(EE) vivodDbl1(SS, TextBox2) |
Рис. 4.6.2-15. Пример обращения к процедуре Pr6214()
Примера 4.6.2-6
Тестовые задания
1. Оператор Dо…Lооp – это:1) оператор итеративного цикла;2) оператор выбора3) оператор регулярного цикла4) составной оператор.2. В итеративной циклической структуре число повторений операторов тела цикла1) может быть известно заранее2) заранее неизвестно3) заранее известно или может быть предварительно вычислено4) нет верного ответа3. Телом цикла в операторе Do…Loop могут быть1) только оператор условного перехода или оператор присваивания2) только арифметические или логические выражения3) любые операторы4) нет верного ответа4. Для досрочного прекращения итеративного цикла используется оператор1) Exit Do2) Exit3) Break4) нет верного ответа5. Алгоритмическая структура цикла итеративного типа может быть1) с предусловием или с постусловием2) только с предусловием3) только с постусловием4) безусловная6. Если при программировании циклической структуры используется операторDo while…Loop, то тело цикла1) обязательно выполнится хотя бы 1 раз2) выполняется заданное число раз3) оператор не относится к средствам программирования итеративного цикла4) может ни разу не выполниться7. Если при программировании циклической структуры используется операторDo…Loop While, то тело цикла1) обязательно выполнится хотя бы 1 раз2) может ни разу не выполниться3) выполняется заданное число раз4) оператор не относится к средствам программирования итеративного цикла8. Если при программировании циклической структуры используется оператор Do…Loop Until, то тело цикла1) обязательно выполнится хотя бы 1 раз2) может ни разу не выполниться3) выполняется заданное число раз4) оператор не относится к средствам программирования итеративного цикла
9. После ключевых слов While или Until в операторе итеративного цикла Do…Loop записывается1) арифметическое или логическое выражение2) оператор выбора3) любой оператор4) нет верного ответа10. Результатом работы фрагмента программы
| Dim n As Integer n = 0 Do While n < 5 n = n + 1 Loop TextBox1.Text = CStr(n) |
| Dim n As Integer n = 0 Do Until n < 5 n = n + 1 Loop TextBox1.Text = CStr(n) |
| i = 1 DO i = i + 2 TextBox1.Text = CStr(i) & vbCrLf LOOP WHILE i < 7 |
16. Определить выходные значения переменных А и С после выполнения алгоритма
4.6.4. Лабораторная работа по теме
«Программирование алгоритмов итеративных
циклических структур»
Цель данной лабораторной работы состоит в получении практических навыков формализации, разработки, написания и отладки проектов, использующих итеративные циклические структуры.
Вопросы, подлежащие изучению
1)Алгоритмы организации итеративных циклических структур: цикл с предусловием; цикл с постусловием.
2)Базовые алгоритмы, использующие итеративные циклические структуры: алгоритм вычисления суммы (или произведения) членов бесконечной последовательности; алгоритмы вычислений по итеративным формулам.
3)Операторы, реализующие выполнение итеративных циклов: Do While…Loop; Do Until…Loop; Do...Loop While…; Do…Loop…Until.
Общее задание на разработку проекта
1) Изучите вопросы программирование алгоритмов итеративных
циклических структур (Тема 6).
2) Создайте приложение с именем Проект-4.6.
3) Выберите вариант задания из таблицы табл. 4.6.4-1.
4) Проведите формализацию поставленной задачи.
5) Разработайте графический интерфейс пользователя. Предусмотрите отображение на форме номера итерации и значения вычисляемого члена бесконечной последовательности или корня уравнения.
6) Разработайте схемы алгоритмов решения поставленной задачи.
7) Напишите программный код процедур пользователя в соответствии со схемами алгоритмов. Обмен данными между процедурами должен осуществляться через параметры, без использования глобальных переменных. Событийная процедура должна содержать только операторы вызова пользовательских (общих) процедур.
8) Выполните созданный проект.
9) полученных результатов на заранее разработанных тестах.
Варианты индивидуальных заданий
Таблица 4.6.4-1
| № | Задача |
| 1) | Вычислите с точностью ε = 0.00001 константу Эйлера (основание натурального логарифма), воспользовавшись разложением в ряд: 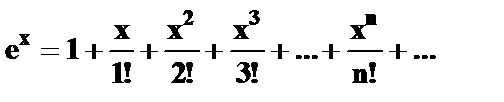 Сравните результат со значением, полученным с помощью соответствующей встроенной функции. Сравните результат со значением, полученным с помощью соответствующей встроенной функции. |
| 2) | Вычислите и выведите те члены последовательности 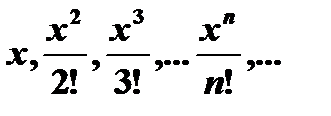 , значения, которых больше ε = 0.001при x = 0.2 , значения, которых больше ε = 0.001при x = 0.2 |
| 3) | Вычислите с точностью ε = 0.00001 значение функции 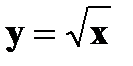 при x = 2, воспользовавшись рекуррентной формулой: при x = 2, воспользовавшись рекуррентной формулой: 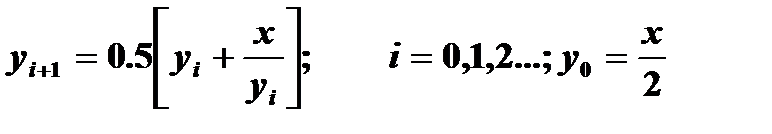 Сравните результат со значением, полученным с помощью соответствующей встроенной функции. Сравните результат со значением, полученным с помощью соответствующей встроенной функции. |
| 4) | Вычислите и выведите те члены последовательности, 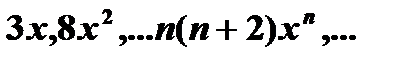 значения которых больше ε = 0.01, при x = 0.6 значения которых больше ε = 0.01, при x = 0.6 |
| 5) | Вычислите константу с точностью до ε = 0.00001, воспользовавшись разложением в ряд: 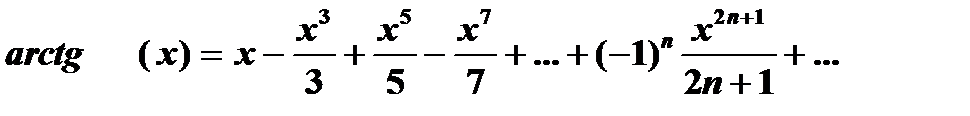 и соотношением и соотношением  Сравните результат со значением, полученным с помощью соответствующей встроенной функции. Сравните результат со значением, полученным с помощью соответствующей встроенной функции. |
| 6) | Вычислите с точностью ε = 0.00001 значение функции 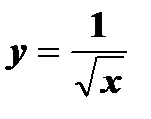 при x = 2, воспользовавшись формулой: при x = 2, воспользовавшись формулой: 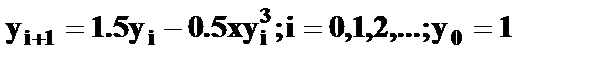 Сравните результат со значением, полученным с помощью соответствующей встроенной функции Сравните результат со значением, полученным с помощью соответствующей встроенной функции |
| 7) | Вычислите sin 0.5с точностью ε = 0.0001, воспользовавшись разложением в ряд: 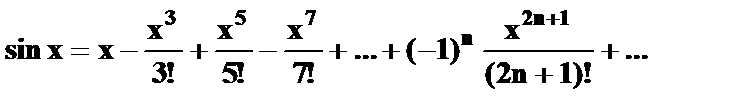 Сравните результат со значением, полученным с помощью соответствующей встроенной функции. Сравните результат со значением, полученным с помощью соответствующей встроенной функции. |
| 8) | Вычислить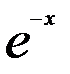 с точностью ε = 0.00001, воспользовавшись разложением в ряд: с точностью ε = 0.00001, воспользовавшись разложением в ряд: 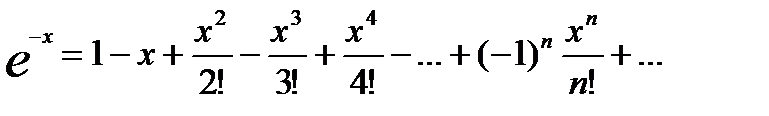 Сравнить результат со значением, полученным с помощью соответствующей встроенной функции. Сравнить результат со значением, полученным с помощью соответствующей встроенной функции. |
| 9) | Вычислите cos(0.6) с точностью ε = 0.00001, воспользовавшись разложением в ряд: 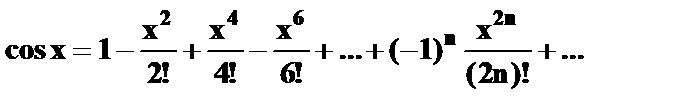 Сравните результат со значением, полученным с помощью соответствующей встроенной функции. Сравните результат со значением, полученным с помощью соответствующей встроенной функции. |
| 10) | Вычислите с точностью ε = 0.0001 корень уравнения 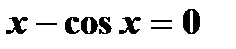 воспользовавшись формулой: воспользовавшись формулой: 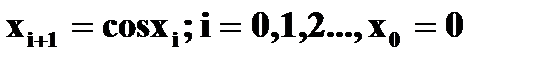 Проверьте правильность решения подстановкой найденного корня в уравнение. Проверьте правильность решения подстановкой найденного корня в уравнение. |
| 11) | Вычислите и выведите те члены последовательности, 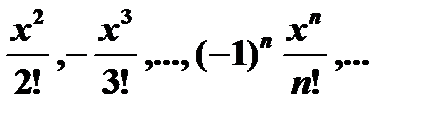 значения, которых по модулю больше ε = 0.001 при x = 0.5. значения, которых по модулю больше ε = 0.001 при x = 0.5. |
| 12) | Вычислить 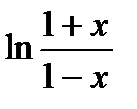 при |x|<1 с точностью до ε = 0.0001, воспользовавшись разложением в ряд: при |x|<1 с точностью до ε = 0.0001, воспользовавшись разложением в ряд: 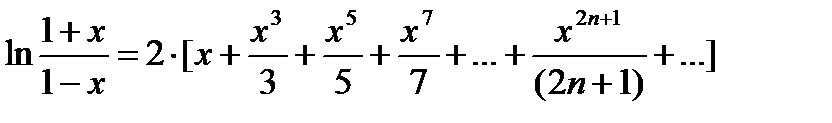 Сравнить результат со значением, полученным с помощью соответствующей встроенной функции. Сравнить результат со значением, полученным с помощью соответствующей встроенной функции. |
| 13) | Вычислите корень уравнения 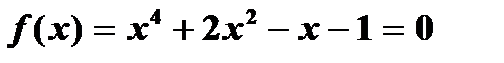 с точностью ε=0.0001, воспользовавшись итерационной формулой с точностью ε=0.0001, воспользовавшись итерационной формулой 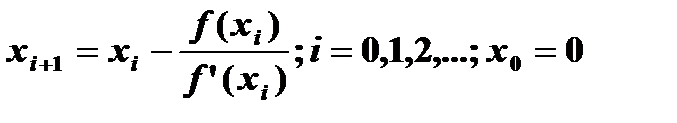 Проверьте правильность решения подстановкой найденного корня в уравнение. Проверьте правильность решения подстановкой найденного корня в уравнение. |
| 14) | Вычислите значение 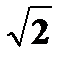 с точностью ε = 0.00001, воспользовавшись представлением в виде цепной дроби: с точностью ε = 0.00001, воспользовавшись представлением в виде цепной дроби: 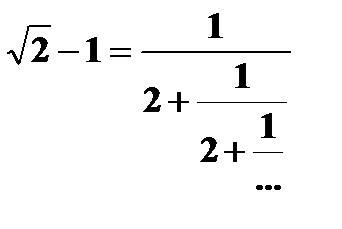 Значение дроби равно пределу числовой последовательности, члены которой вычисляются по рекуррентной формуле до достижения заданной точности Значение дроби равно пределу числовой последовательности, члены которой вычисляются по рекуррентной формуле до достижения заданной точности 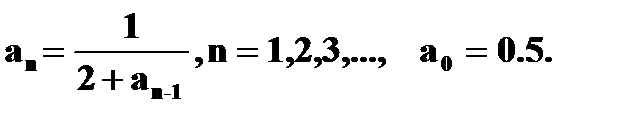 . Сравните результат со значением, полученным с помощью соответствующей встроенной функции. . Сравните результат со значением, полученным с помощью соответствующей встроенной функции. |
| 15) | Вычислите и выведите те члены последовательности, 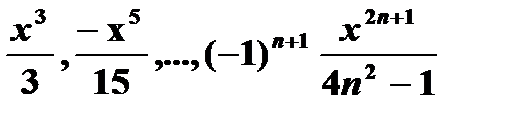 значения, которых по модулю больше ε = 0.001 при x = 0.3. значения, которых по модулю больше ε = 0.001 при x = 0.3. |
| 16) | Вычислитьln(x) с точностью ε = 0.0001, воспользовавшись разложением в ряд: 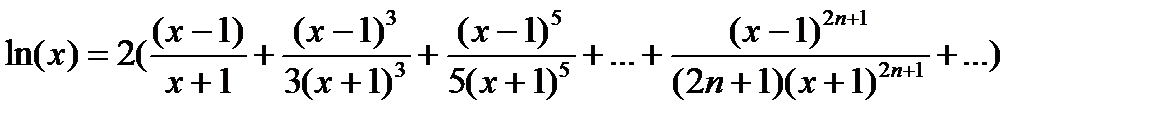 Сравнить результат со значением, полученным с помощью соответствующей встроенной функции при x=1.5. Сравнить результат со значением, полученным с помощью соответствующей встроенной функции при x=1.5. |
| 17) | Вычислите sh(0.3) с точностью до ε= 0.00005, воспользовавшись разложением в ряд: 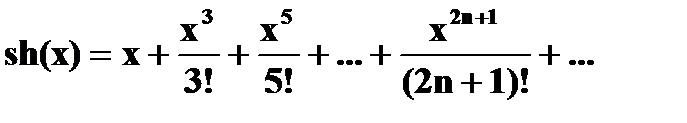 Сравните результат со значением, полученным с помощью встроенной функции для вычисления ex, используя соотношение: Сравните результат со значением, полученным с помощью встроенной функции для вычисления ex, используя соотношение: 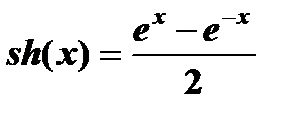 |
| 18) | Вычислите корень уравнения x-0.5(sinx2-1)=0 с точностью ε = 0.001, воспользовавшись итерационной формулой: 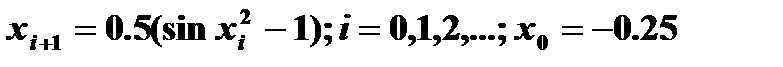 Проверьте правильность решения подстановкой найденного корня в уравнение. Проверьте правильность решения подстановкой найденного корня в уравнение. |
| 19) | Вычислите ln(2) с точностью ε = 0.001, воспользовавшись представлением в виде ряда: 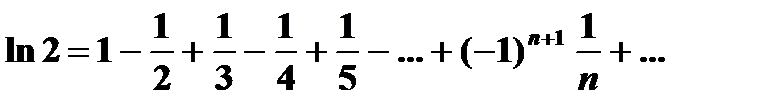 Сравните результат со значением, полученным с помощью встроенной функции. Сравните результат со значением, полученным с помощью встроенной функции. |
| 20) | Вычислите с точностью ε = 0.00001 корень уравнения 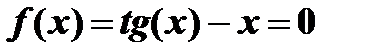 воспользовавшись итерационной формулой воспользовавшись итерационной формулой 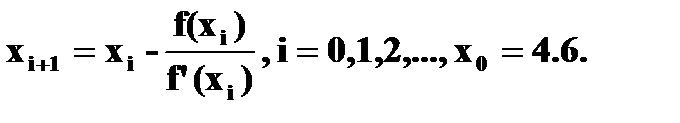 Проверьте правильность решения подстановкой найденного корня в уравнение. Проверьте правильность решения подстановкой найденного корня в уравнение. |
| 21) | Вычислите ch 0.7 с точностью до ε = 0.00005, воспользовавшись разложением в ряд: 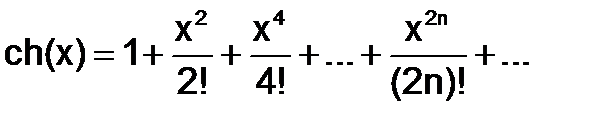 Сравните результат со значением, полученным с помощью встроенной функции Сравните результат со значением, полученным с помощью встроенной функции 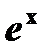 , используя соотношение: , используя соотношение: 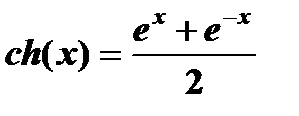 |
| 22) | Пусть 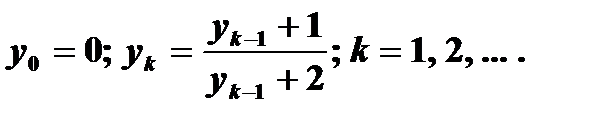 Дано действительное число e>0. Найдите первый член Дано действительное число e>0. Найдите первый член 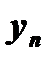 , для которого выполнено условие , для которого выполнено условие 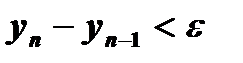 . . |
| 23) | Вычислить 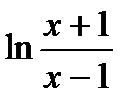 при |x|>1 с точностью до ε = 0.0001, воспользовавшись разложением в ряд: при |x|>1 с точностью до ε = 0.0001, воспользовавшись разложением в ряд: 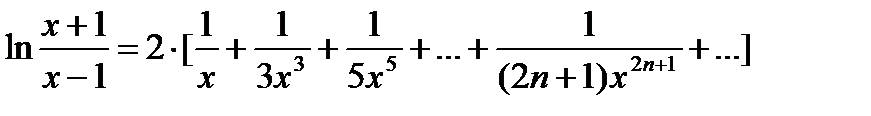 Сравнить результат со значением, полученным с помощью соответствующей встроенной функции. Сравнить результат со значением, полученным с помощью соответствующей встроенной функции. |
| 24) | Вычислитьln(x+1) с точностью ε = 0.0001, воспользовавшись разложением в ряд: 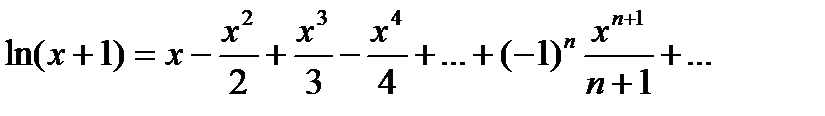 Сравнить результат со значением, полученным с помощью соответствующей встроенной функции при x=0.5. Сравнить результат со значением, полученным с помощью соответствующей встроенной функции при x=0.5. |
| 25) | Дано действительное число b<0. Последовательность а1, а2, …образована по следующему закону: a1=b; ak=(ak-1+1)/(1-sin2k), k=2, 3, … . Найдите первый неотрицательный член последовательности. |
| 26) | Дано действительное число x. Вычислите приближенное значение бесконечной суммы с точностью ε=0,00001: (x-1)/x+(x-1)2/(2x2)+(x-1)3/(3x3)+… (x>1/2) |
| 27) | Дано действительное x. Вычислить приближенное значение 1/x+1/(3x3)+1/(5x5)+… (x>1) бесконечной суммы с точностью ε=0.0001. |
| 28) | Вычислите приближенное значение бесконечной суммы с точностью ε=0,0001 (справа от суммы дается ее точное значение, с которым можно сравнить полученный результат): 1+1/22+1/32+… p2/6 |
| 29) | Вычислите приближенное значение бесконечной суммы с точностью ε=0,0001 (справа от суммы дается ее точное значение, с которым можно сравнить полученный результат): 1-1/3+1/5-1/7+… p/4 |
| 30) | Вычислите приближенное значение бесконечной суммы с точностью ε=0,0001 (справа от суммы дается ее точное значение, с которым можно сравнить полученный результат): 1/(1*3)+1/(2*4)+1/(3*5)+… 3/4 |
4.6.4.4. Содержание отчёта
1)Тема и название лабораторной работы.
2)Фамилия, имя студента, номер группы, номер варианта.
3)Задание на разработку проекта.
4)Формализация и уточнение задания.
5)Элементы, разрабатываемого проекта:
5.1) графический интерфейс пользователя;
5.2) таблица свойств объектов;
5.3) схемы алгоритмов процедур проекта;
5.4) программный код проекта.
6)Результаты выполнения проектов.
7)Доказательство правильности работы проекта.
