Используя правило возведения в степень, получим

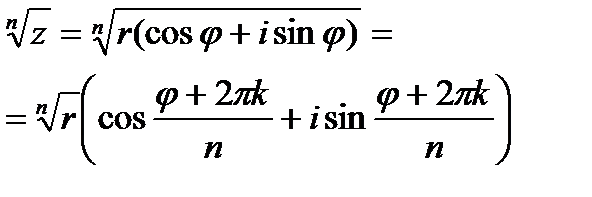, (6.3.4)

где k=0,1,2, …, n-1.

Геометрически эти n значений выражения 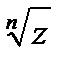изображаются вершинами некоторого правильного n - угольника, вписан­ного в окружность, с центром в -нулевой почке радиуса .

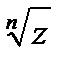С помощью формулы Эйлера можно привести к более простому виду:

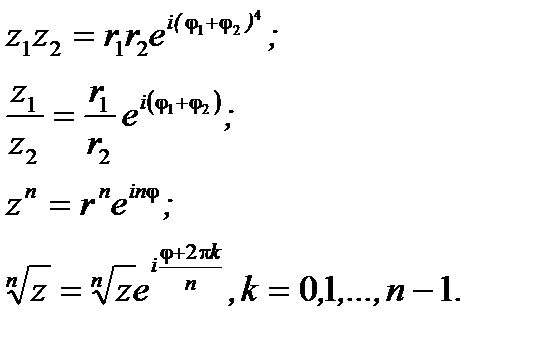
Рассмотрим множества точек на плоскости и дадим некоторые определения.

Определение 6.3.1. Множество точек г комплексной плоскости, удовлетворяющее неравенству 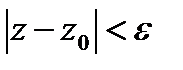, называется e - окрестностью точки z₀.

Определение 6.3.2. Точка r называется внутренней точкой множества Е точек комплексной плоскости, если существует e окрестность точки z, целиком принадлежащая множеству Е.

Определение 6.3.3. Множество Е называется областью, если оно обладает следующими свойствами;

1) каждая точка Е является внутренней;

2) любые две точки, принадлежащие Е, можно соединить ломаной, состоящей ив точек множества Е. Второе свойство в этом определении называют свойством связности области.

Определение 6.3.4. Граничной точкой области G называется точка, не принадлежащая самой области, но любая e, окрестность которой содержит точки G.

Например , z=1 является граничной точкой области .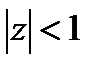

Определение 6.3.5. Совокупность всех граничных точек называется границей области G.

Определение 6.3.6. Область с присоединенной к ней границей называется замкнутой областью и обозначается через .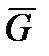

Например, замкнутой областью является множество 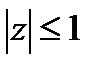Определение 6.3.7. Число связных частей, на которые разбивается область, называется порядком связности области. Например, область 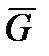- односвязная (рис. 6.3.1.).

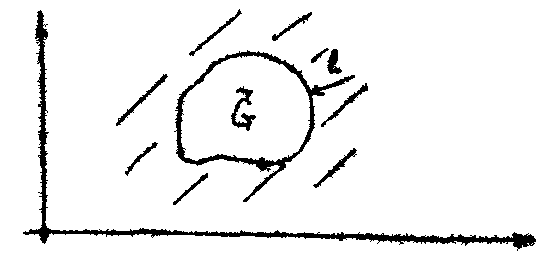
Рис. 6.3.1.

Пусть границей 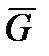является кривая С. Положительным направлением обхода называется такое направление, при котором обходимая область остается слева.

Определение 6.3.8. Область G называется ограниченной, если она лежит внутри некоторого круга конечного радиуса.

Пример 6.3.1.Решить уравнение z²-6z+10=0.

Решение.В результате подстановки z=x+iy в данное уравнение имеем

(x+iy)²-6(x+iy)+10=0 , откуда после преобразований получим систему уравнений

x²-y²-6x+10=0;

xy-3y=0.

Решая систему, получим z₁=x₁+iy₁=3+I ; z₂=x₂+iy₂=3-I.

Пример 6.3.2. Выяснить геометрический смысл модуля разности |z₁-z₂| двух комплексных чисел z₁ и z_{2 .}

Решение. |z₁-z₂ |= | (x₁-x₂)+i(y₁-y₂)|= .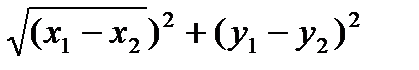

Следовательно, |z₁-z₂ | означает расстояние между точками z₁=x₁+iy₁ и z₂=x₂+iy₂

Если изобразить комплексное число с помощью вектора, то действительная и мнимая части z₁-z₂ являются координатами вектора, а так как при вычислении векторов координаты соответственно вычитаются, то вычитание комплексных чисел сводится к вычитанию векторов, изображающих эти числа

Как видно из рис.1а, | z₁-z₂ | есть длина вектора z₁-z₂=М₂М_1, иначе расстояние между точками ,

Пример 6.3.3. Выяснить, какой геометрический смысл имеет модуль разности двух комплексных чисел.

Решение.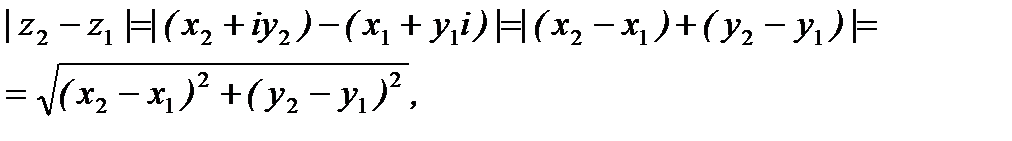

то есть 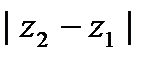равен расстоянию между точками .