Лекція : Інтерполяційні многочлени Ньютона першого і другого виглядів

1. Постановка задачі інтерполювання

2. Поняття про скінчені різниці та їх властивості

3. Інтеропляційний многочлен Ньютона першого вигляду

4. Інтеропляційний многочлен Ньютона другого вигляду

Загальна постановка задачі інтерполювання (інтерполяція – знаходження по ряду значень функції проміжних її значень) полягає у наступному: нехай на відрізку [a;b] в n+1 даних точках x ,x ,…,x відомі значення деякої функції f(x) :

y =f(x ), y =f(x ), …, y =f(x ).

Треба визначити значення функції f(x) в точці хЄ[a;b], що не збігається з даною.

Звичайно, з такою постановкою задачі розв’язок задачі невизначено. Більш конкретно задача інтерполювання функції f(x) полягає в тому, щоб побудувати функцію F(x), що належить певному класу функцій і та що в даних точках х 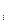набуває тих же значень y 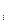=f(x 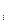), що і функція f(x): F(x 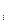)=y (i=0,1,…,n).

Тоді для х Є[a;b] наближено покладають f(x)=F(x).

Точки x ,x ,…,x називають вузлами (чи полюсами ) інтерполяції, а функцію F(x) – інтерполяційною функцією.

Звичайно інтерполяційну функцію шукають серед многочленів P (x), степінь яких не перевищує n і які задовольняють умові P (x )=y =f(x ), P (x )=y =f(x ),...,P (x )=y =f(x ). (1)

Неважко показати, що існує тільки один многочлен P (x) степені не вище n, що задовольняє всі умови (1).

Задача алгебраїчного (параболічного) інтерполювання функції y=f(x) на [a;b] полягає у відшуканні аналітичного вираження многочлена P (x), що задовольняє умові (1).

Многочлен P (x), визначений по умові (1), називається інтерполяційним многочленом для f(x), а формули для її побудови – інтерполяційними формулами.

Заміна функції y=f(x) її інтерполяційним многочленом f(x)=P (x), хЄ[a;b] називається інтерполюванням (алгебраїчним) функції.

Звичайно, при цьому виникає питання про оцінку похибки наближеної формули (2).

Геометричний зміст інтерполювання – заміна кривої y=f(x) параболою y=P (x) (порядка n), що проходить через задані точки (x ;y ), (х1;у1),...,(х_n;y_n).

Формулу (2) вважають інтерполяційною, якщо хЄ[x ;x ], тобто знаходиться між вузлами інтерполяції, якщо ж х 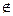[x ;x ], тобто знаходиться зовні відрізка, то формулу (2) називають екстраполяцією. В дальнішому ця відміність не враховується.

Визначення скінчених різниць.

Нехай функція представлена у вигляді таблиці:

Х0	Х1	...	Хі	...	Хn
Y0	Y1	...	Yi	...	Yn

Вузли інтерполяції рівностоящі з кроком h, тобто х₁=х₀+h, x₂=x₀+2h, ..., x_n=x_n-1+h=x₀+nh. Різниці

y₁-y₀= y₀,

y₂-y₁= y_1,

_{.........................} (1)

y_i+1-y_i= y_i,

_{........................,}

y_n-y_n-1= y_n-1.

називаються скінченими різницями першого порядку.

Різниці перших скінчених різниць y₁- y₀= ²y₀, y₂- y₁= ²y₁,..., y_і+1- y_і= ²y_і,..., y_n-1- y_n-2= ²y_n-2 (2)

називають скінченими різницями другого порядку. В загальному, скінчені різниці k-го порядку визначаються через різниці (k-1)-го порядку по формулах

^k-1y₁- ^k-1y₀= ^ky₀,

^k-1y₂- ^k-1y₁= ^ky_1,

_{............................................,} (3)

^k-1y_i+1- ^k-1y_i= ^ky_i, (k=(1,n) ; ⁰y=y).

...........................,

^k-1y_n-(k-1)- ^k-1y_n-k= ^ky_n-k ,

Формули (3) носять рекурентний характер, вони виражають різницю k-го порядку через різниці (k-1) порядку. Однак послідовні наближення можна виразити і безпосередньо через значення функції. Дійсно, із формули (1) слідує, що y_i=y_i+1-y_i=у(х_і+h)-y(x_i). Далі із формули (2), враховуючи (1), знаходимо

y²_i= y_і+1- y_і=(у_і+2-у_і+1)-(у_і+1-у_і)=у_і+2-2у_і+1+у_і=у(х_і+2h)-2y(x_i+h)+y(x_i) і так далі. В загальному

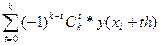^ky_i= , де 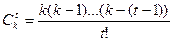- біномінальний коефіцієнт (0!=1)

Нерідко буває корисні обернені формули, які дають вирази значень функції через скінчені різниці. Із співвідношення (1) випливає, що у₁=у₀+ y₀, аналогічно у₂=у₁+ y₁=(у₀+ y₀)+ y₁, Але враховуючи (2), ²y₀= y₁- y₀ і у₂=у₀+2 y₀+ ²y₀.

Розмірковуючи аналогічно, можна визначити значення у_k при любому k через y₀ і різниці до k-го порядку:

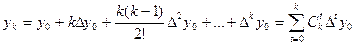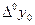, де =у_0.

Перерахуємо деякі властивості скінчених різниць:

1) 1) Якщо с=const, то с=0;

2) 2) (cf(x))=c f(x);

3) 3) (f₁(x)+f₂(x))= f₁(x)+ f₂(x);

4) 4) ^m( ⁿf(x))= ^m+nf(x).

Користуючись цими властивостями для многочлена y=P_n(x)=a₀xⁿ+a₁x^n-1+...+a_n-1x+a_n. Знаходимо першу різницю

у= P_n(x)=a₀ (xⁿ)+a₁ (x^n-1)+...+a_n-1 (x).

Враховуючи, що (хⁿ)= (x+h)-xⁿ=nhx^n-1+ 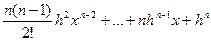, одержимо

P_n(x)=a₀nhx^n-1+(a_{0 .}

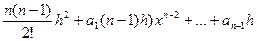Таким чином, перша різниця многочлена степені n зі старшим членом а₀хⁿ є многочлен степені n-1 зі старшим членом а₀nhx^n-1. Обчислюючи аналогічним чином різниці любого порядку, впевнимось у справедливості наступного твердження: Якщо Р_n(x)- многочлен степені n зі старшим членом а₀хⁿ, то для любого k<n різниця ^kP_n(x) є многочлен степені n-k зі старшим членом n(n-1)...(n-k+1)a₀h^kx^n-k; різниця n-го порядку постійна, а для k>n різниця рівна нулю.

Справедливе і обернене твердження: якщо n різниця функції для рівностоящих значень аргумента при любому кроці h постійна, то функція представляє собою многочлен степені n.

Практично постійними вважаються такі різниці, які відрізняються одна від другої менше, чим на 5 одиниць молодшого розряду таблично заданої функції. Якщо для деякої функції різниці n порядку практично постійні, то функцію приблизно можна представити многочленом степені n.

3. Інтеропляційний многочлен Ньютона першого вигляду. Ми розглядали інтерполяційну формулу Лангранжа, яка будувалась при будь-якій кількості вузлів інтерполяції. Однак, якщо треба буде добавити ще один вузол інтерполяції, то всі коефіцієнти Лангранжа треба заново перерахувати. Цієї незручності немає приведена нижче формула Ньютона, яка хоче рівновіддалених вузлів.

Ітак, нехай задані вузли інтерполяції з кроком h: x₀,x₁=x₀+h, x₂=x₀+2h, ...,x_n=x₀+nh.

Розглянемо многочлен степені n, записаний у вигляді:

P_n(x)=q₀+q₁(x-x₀)+...+q_k(x-x₀)...(x-x_k-1)+...+q_n(x-x₀)...(x-x_n-1) (1) і визначемо його коефіцієнти q₀, q₁..., q_k,...,q_n.

Поставимо в (1) х=х₀, тоді P_n(x₁)=q_n+q₁(x₁-x₀), P_n(x₁)=y₁=y₀+q₁(x₁-x₀), q₁= ;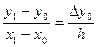

Потім при х=х₂ одержимо

P_n(x₂)=q₀+q₁(x₂-x₀)+q₂(x₂-x₀)(x₂-x₁);

y₂=y₀+ 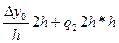, у₂-у₀-2 у₀=q₂2h²;

q₂= .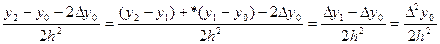

Аналогічно, одержимо q₃= 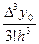, ..., q_k= 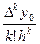, ...,q_n= .

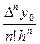Підставляючи всі одержані коефіцієнти у (1), тоді

P_n(x)=y₀+ 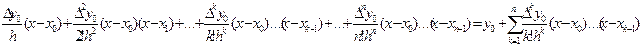. (2)

Це і буде перша інтерполяційна формула Ньютона. Інтерполяційний многочлен (2), очевидно, має степінь n, але на відміну від многочлена Лагранжа, степені його членів постійно підвищуються. Тому добавлення одного вузла інтерполяції добавить лише один доданок в (2), але не змінить всіх решта. Перевага многочлена Ньютона перед многочленом Лагранжа полягає ще в тому, що в формулі (2) знаменники коефіцієнтів містять k!. Ці числа зі збільшенням k різко зростають, а відповідно, коефіцієнти зменшуються і при обчисленні, починаючи з деякого номера, решта членами (більш високих степенів) можна знехтувати. Що ж стосується многочлена Лагранжа, то в ньому члени рівноправні, однакової степені n і при будь-яких обчисленнях повинні бути присутні.

Замітимо, що якщо при побудові многочлена Лангранжа і Ньютона вузли інтерполяції співпадають, то многочлени будуть тотожньо рівні (рівні коефіцієнти при однакових членах). Це слідує із єдиності побудови многочлена степені n.

Надамо формулі (2) деякий інший вигляд, ввівши змінну t= 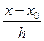. Оскільки x-x₀=th, x-x₁=x-x₀-h=th-h=(t-1)h, x-x₂=(t-2)h,…,x-x_n-1=(t-(n-1))h, то підставивши одержані значення в (2), маємо

P_n(x)=P_n(x₀+th)=y₀+ 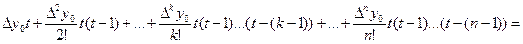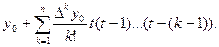(3)

Це і є кінцевий вигляд першої інтерполяційної формули Ньютона. Поклавши в формулі (3) n=1, одержимо лінійну інтерполяцію P₁(x)=P₁(x₀+th)=y₀+ y₀t, а при n=2 – квадратну P₂(x)=P₂(x₀+th)=y₀+ y₀t+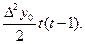

В загальному на практиці n вибирають виходячи із того, що різниці 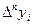наближено постійні з заданою степеню точності. Остаточний член формули (2) можна оцінювати так само, як і формули Лагранжа.

Враховуючи, що вузли інтерполяції рівновіддалені, і враховуючи, що многочлен Ньютона записаний у вигляді (3), маємо 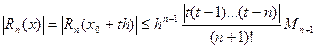(4), де М_n+1=max 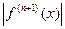, a x b.

Коли вираз f⁽ⁿ⁺¹⁾(x) невідомий, але є додатковий вузол інтерполяції хⁿ⁺¹ для оцінки R_n(x), то користуються формулою 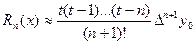, 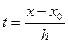(5).

Звідси отримуємо дуже зручну оцінку похибки лінійної інтерполяції

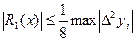, де 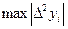найбільше значення модуля других різниць.

4. Інтеропляційний многочлен Ньютона другого вигляду.

Формулу

P_n(x)=y₀+ 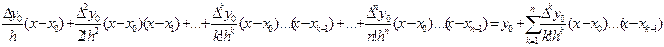або

P_n(x)=P_n(x₀+th)=y₀+ 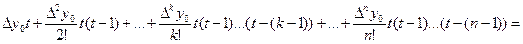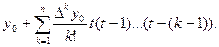називають інтерполяційною формулою інтерполювання вперед, так як вона будується з використанням значення функції і її різниць в початковому вузлі інтерполяції х₀. ЇЇ зазвичай застосовують при інтерполяції в точках х, близьких до х₀ ( для зменшення похибки інтерполювання ). Якщо ж потрібно інтерполювати в точках х, близьких до вузла інтерполяції х_n, то краще користуватися так званою формулою для інтерполяції назад. Для виводу її представимо P_n(х) у вигляді

P_n(x)=b₀+b₁(x-x_n)+b₂(x-x_n)(x-x_n-1)+…+b_k(x-x_n)…(x-x_n-(k-1))+…b_n(x-x_n)…(x-x₁). (6)

Підставляючи в формулу (6) послідовно х=х_n, x=x_n-1, …, x=x₀. Отримаємо х=х_n, P_n(x_n)=b₀, b₀=P_n(x_n)=y_n;

x=x_n-1, P_n(x_n-1)=y_n-1=b₀+b₁(x_n-1-x_n)=b₀-b₁h, y_n-1-y_n=-b₁h, b₁= ;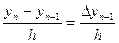

x=x_n-2, P_n(x_n-2)=y_n-2=b₀+b₁(x_n-2-x_n)+b₂(x_n-2-x_n)(x_n-2-x_n-1), y_n-2-y_n+ 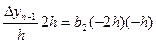, b₂= 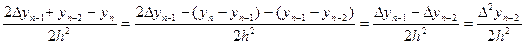. Аналогічно маємо b₃= 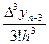,…, b_n= .

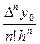Формула (6) при знайдених коефіцієнтах прийме вигляд P_n(x)=y_n+ 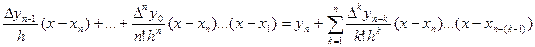(7). Це і буде друга інтерполяційна формула Ньютона. Якщо ж ввести нову змінну t, поклавши t= 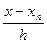, то з (7) отримаємо інший вигляд другої інтерполяційної формули Ньютона: P_n(x)=P_n(x_n+th)=y_n+ 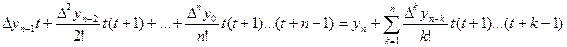. (8)

Оцінка останнього члена формули (7): 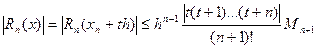, де М_n+1=max 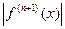, a x b.

Використовуючи скінчені різниці при додатковому вузлі інтерполяції можна сказати, що 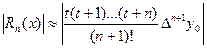.