Классификация классов по Ассуру-Артоболевскому

Классы механизмов определяются по наивысшему классу структурной группы, входящих в его состав.

Для определения классов механизмов необходимо его КЦ разложить на структурные группы и ведущие звенья.

Эта операция называется структурным анализом. Перед проведением структурного анализа необходимо исключить лишние степени свободы и избыточные связи, а так же осуществить замену высших пар низшими.

При проведении структурного анализа сначала следует попытаться отсоединить структурные группы 2 класса, наиболее удалённые от КЦ от ведущего звена.

Если это невозможно без того, чтобы оставшееся КЦ была бы механизмом с тем же числом степеней свободы, что и исходный механизм, то следует попытаться оценить группы 3 класса и так далее. В итоге должно остаться число ведущих звеньев, равное числу степеней свободы, исходного механизма.

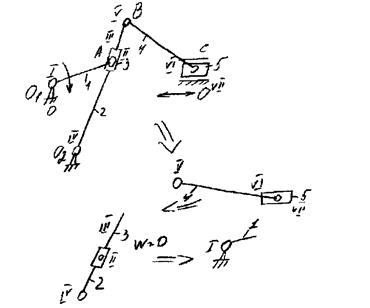Пример:

n=5 P5=7 P4=0

Ошибка! Объект не может быть создан из кодов полей редактирования. Ошибка! Объект не может быть создан из кодов полей редактирования.

Записывается формула строения механизма, условная запись, показывается в какой последовательности к ведущему звену присоединяться структурные группы преобразования механизма:

2.1 Основные механизмы современной техники

С развитием современной науки и техники все шире исполь­зуются системы машин автоматического действия. Совокупность машин-автоматов, соединенных между собой и предназначенных для выполнения определенного технологического процесса, назы­вается автоматической линией.

Развитые системы машин являются комплексом машин различ­ных классов. Так, например, современные роторные и другие автоматические линии являются комплексом, в который входят энергетические машины в виде электроприводов, транспортные машины для перемещения обрабатываемого объекта в виде роторов или транспортеров, технологические машины, изменяющие форму, состав или структуру обрабатываемого объекта, контрольно-упра­вляющие машины, контролирующие качество и размеры получае­мых изделий и регулирующие режим движения двигателей и ра­бочих органов, и, наконец, логические машины, производящие подсчет количества выпускаемой продукции. В некоторых разви­тых машинных устройствах функции контроля и управления, а также логические функции могут выполняться не специальными машинами, а соответствующими приборами и системами, органиче­ски входящими в состав машинного устройства. Так, например, автомат для шлифования изделий с помощью шлифовального круга, представляющий собой технологическую машину, имеет в своем составе электропривод, являющийся энергетической машиной, и управляющее устройство, автоматически компенсирующее износ шлифовального круга. Фрезерный станок-автомат, представляю­щий собою технологическую машину, имеет в своем составе элек­тропривод, т. е. энергетическую машину, систему программного управления, являющуюся управляющим устройством, систему конт­роля точности изготовления изделия и, наконец, систему перера­ботки информации в виде счетно-решающего устройства, коррек­тирующего процесс. Даже простейшие машинные устройства, как, например, паровая машина, имеют систему автоматического регу­лирования и управления в виде, например, центробежного регуля­тора.

Развитое машинное устройство, состоящее из двигателя, пере­даточных механизмов и рабочей машины и в некоторых случаях контрольно-управляющих и счетно-решающих устройств, назы­вается машинным агрегатом.

4°. При создании машины человек пользуется всеми достиже­ниями математики, механики, физики, химии, электротехники и электроники. Машины могут работать и осуществлять требуемые движения своих органов с помощью устройств, в основе которых лежат различные принципы воспроизведения движения, производ­ства работы и преобразования энергии. Современные наиболее раз­витые и совершенные машины обычно представляют собою совокуп­ность многих устройств, в основу работы которых положены прин­ципы механики, теплофизики, электротехники и электроники.

Наука, изучающая машины, в основе работы которых поло­жены принципы механики с точки зрения исследования законов движения отдельных устройств и действующих на них сил, носит название «механики машин».

Система тел, предназначенная для преобразования движения одного или нескольких тел в требуемые движения других тел, назы­вается механизмом. Механизмы, входящие в состав машины, весьма разнообразны. Одни из них представляют собою сочетания только твердых тел. Другие имеют в своем основном составе гидравличе­ские, пневматические тела или электрические, магнитные и другие устройства. Соответственно такие механизмы называются гидравли­ческими, пневматическими, электрическими и т. д. С точки зрения их функционального назначения механизмы машины обычно де­лятся на следующие виды:

а) механизмы двигателей и преобразователей,

б) передаточные механизмы,

в) исполнительные механизмы,

г) механизмы управления, контроля и регулирования,

д) механизмы подачи, траспортировки, питания и сортировки
обрабатываемых сред и объектов,

е) механизмы автоматического счета, взвешивания и упаковки
готовой продукции.

Механизмы двигателей осуществляют преобразование различ­ных видов энергии в механическую работу. Механизмы преобразо­вателей (генераторов) осуществляют преобразование механической работы в другие виды энергии. К механизмам двигателей относятся механизмы двигателей внутреннего сгорания, паровых машин, электродвигателей, турбин и др. К механизмам преобразова­телей относятся механизмы насосов, компрессоров, гидроприво­дов и др.

Передаточные механизмы (привод) имеют своей задачей передачу движения от двигателя к технологической машине или исполнитель­ным механизмам. Так как вал двигателя обычно имеет большее число оборотов в минуту, чем основной вал технологической ма­шины, задачей передаточных механизмов является уменьшение числа оборотов в минуту вала двигателя до уровня числа оборотов в минуту основного вала технологической машины.

Исполнительными механизмами называются те механизмы, кото­рые непосредственно воздействуют на обрабатываемую среду или объект. В их задачу входит изменение формы, состояния, положе­ния и свойств обрабатываемых среды или объекта. К исполнитель­ным механизмам, например, относятся механизмы прессов, дефор­мирующих обрабатываемый объект, механизмы грохотов в энерго­зерноочистительных машинах, разделяющих среду, состоящую из зерна и соломы, механизмы металлообрабатывающих станков, изменяющие форму заготовки снятием стружки до той формы, которая требуется по технологическим условиям, механизмы про­ката слитков в блюмингах и т. д.

Механизмами управления, контроля и регулирования назы­ваются различные механизмы и устройства для контроля размеров обрабатываемых объектов, например механические щупы, сле­дующие за фрезой, обрабатывающей криволинейную поверхность, и сигнализирующие об отклонении фрезы от заданной программы обработки; регуляторы, реагирующие на отклонение угловой скорости главного вала машины и устанавливающие нормальную заданную угловую скорость этого вала; механизм, регулирующий постоянство расстояния между валками прокатного стана и т. д. К этим же механизмам относятся и измерительные механизмы по контролю размеров, давления, уровней жидкостей и т. д.

К механизмам подачи, транспортировки, питания и сортировки обрабатываемых сред и объектов относятся механизмы винтовых шнеков, скребковых и ковшевых элеваторов для транспортировки и подачи сыпучих материалов, механизмы загрузочных бункеров для штучных заготовок, механизмы подачи пруткового материала в высадочных автоматах, механизмы сортировки готовой продук­ции по размерам, весу и конфигурации и т. д.

Механизмы автоматического счета, взвешивания и упаковки готовой продукции применяются во многих машинах, в основном выпускающих массовую штучную продукцию. Необходимо иметь в виду, что такие механизмы, как механизмы счета, взвешивания и упаковки готовой продукции, могут быть и исполнительными меха­низмами, если они входят в специальные машины, предназначае­мые для этих операций.

Так, например, в машинах для расфасовки чая механизмы взвешивания и упаковки являются исполнительными механизмами. В промышленности, изготовляющей шарикоподшипники, имеются специальные машины для упаковки собранных шарикоподшипни­ков, в которых механизмы упаковки являются исполнительными механизмами, и т. д.

Несмотря на разницу в функциональном назначении механиз­мов отдельных видов, в их строении, кинематике и динамике много общего.

Например, механизм поршневого двигателя, механизм кривошипного пресса и механизм привода ножа косилки имеют в своей основе один и тот же кривошипно-ползунный механизм. Механизм привода резца строгального станка и механизм ротор­ного насоса имеют в своей основе один и тот же кулисный меха­низм. Механизм редуктора, передающего движение от двигателя самолета к его винту, и механизм дифференциала автомобиля имеют в своей основе зубчатый механизм и т. д.

Поэтому можно к исследованию механизмов с различными функциональными назначениями применять общие методы, бази­рующиеся на основных принципах современной механики. В меха­нике обычно рассматриваются статика, кинематика и динамика как абсолютно твердых, так и упругих тел. При исследовании машин и механизмов, как правило, мы можем считать жесткие тела, обра­зующие механизм, абсолютно твердыми, так как перемещения, возникающие от упругих деформаций тел, малы по отношению к пе­ремещениям самих тел и их точек. Если мы рассматриваем меха­низмы как устройства, в состав которых входят только твердые тела, то для исследования кинематики и динамики механизмов можно пользоваться методами, излагаемыми в теоретической меха­нике. Если же требуется изучить кинематику и динамику механиз­мов с учетом упругости звеньев, то для этого, кроме методов тео­ретической механики, мы должны еще применять методы, излагае­мые в сопротивлении материалов, теории упругости и теории колебаний. Если в состав механизма входят жидкие или газо­образные тела, то необходимо привлекать к исследованию

2.2 Основные понятия и определения: кулачёк, ведомое звено. Виды кулачковых механизмов.

Кулачковым называется механизм, который содержит два основных звена: кулачок и толкатель, образующих высшую кинематическую пару.

Кулачковые механизмы нашли широкое применение в системах газораспределения ДВС, в системах управления электроцепей в вагонах метрополитена (контроллеры).

Достоинства кулачковых механизмов:

1. возможность воспроизведения практически любого закона движения выходного звена;

2. малое количество деталей (кулачок и толкатель), что позволяет просто изготавливать и обслуживать.

Недостаток:

наличие высшей кинематической пары, в которой могут возникать повышенные удельные давления, что может привести к разрушению поверхности кулачка.

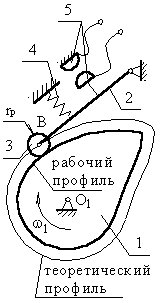
1 – кулачок

2 – толкатель

3 – ролик

4 – пружина

5 – контакты

Поверхность кулачка, с которой взаимодействует толкатель – рабочий профиль кулачка (действительный).

Поверхность, проходящая через точку В и отстоящая от действительного профиля на расстоянии радиуса ролика – теоретический профиль.

§6.1 Основные схемы кулачковых механизмов.

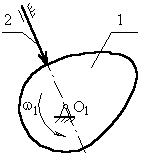
1.1.1 Кулачковый механизм с поступательно движущимся толкателем.

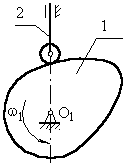а) с центральным толкателем (ось толкателя проходит через ось вращения кулачка);

с заостренным

толкателем

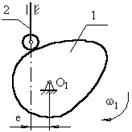
б) с внеосным толкателем.

е – эксцентриситет

внеосность левая, т.к. ось толкателя проходит справа оси вращения кулачка.

6.1.2 Кулачковый механизм с поступательно движущимся

толкателем.

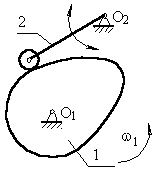
звено 2 (толкатель) совершает возвратно­­–вращающееся движение с центром вращения в точке О₂.

2.1-2.8 Кулачковые механизмы

КУЛАЧКОВЫЕ МЕХАНИЗМЫ

Для определения минимального радиуса г„ профиля кулачка для механизма с коромыслом применяется следующий способ (рис. 136). Пусть задана диаграмма ер₂ = ф₂ (ф_г) угла поворота коромысла в функции угла поворота кулачка и диаграммы ф^ = = Фа (фг) — аналога угловой скорости коромысла в функции того же угла. Для решения задачи строим отдельные положения коро­мысла, пользуясь первой диаграммой. На вычерченных лучах сле­дует отложить от дуги, описанной концом коромысла, соответству­ющие положительные величины аналога ф_а', умноженные на длину коромысла. Полученные точки обводят плавной кривой. После этого в положениях, близких к максимальным величинам аналога %, под углом 90° — ймакс проводят прямые, левее которых можно выбирать место для центра вращения кулачка.

Описанные построения сходны с изложенными выше постро­ениями для механизма с толкателем. В рассматриваемом случае механизм с коромыслом можно рассматривать в качестве механизма с толкателем, имеющим переменный эксцентриситет. Здесь эксцен­триситет является перпендикуляром, опущенным из центра враще-«ия кулачка на линию действия вектора скорости конца коромысла.

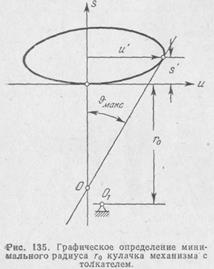На рис. 136 величина эксцентри­ситета е показана для одного из положений механизма. Чтобы в этом положении получился заданный максимальный угол давления, центр вращения ку­лачка следует поместить в точке Оц находящейся на линии дей­ствия аналога скорости и. Если центр вращения кулачка нахо­дится ниже и левее этой точки, то угол давления оказывается меньше указанного. Выполнив описанные построения в левой части кривой для нескольких положений коромысла, мы полу­чаем границу, правее которой нельзя выбирать место для центра вращения кулачка.

Все рассмотренные характе­ристики следует принимать во

внимание при выборе закона движения ведомого звена кулачкового механизма.

6°. У механизма с плоским толкателем, плоскость которого перпендикулярна к оси его движения, угол давления во всех по­ложениях остается равным нулю, ибо линия действия силы, при­ложенной со стороны кулачка к толкателю, совпадает с нормалью к профилю и плоскости. Эта нормаль параллельна оси движения. Таким образом, размеры кулачка не влияют на величину угла дав-.ления, она остается во всех положениях равной нулю (рис. 137). Но линия действия силы, приложенной к толкателю, параллельна направляющей и только в одном положении совпадает с ней. Вслед­ствие этого толкатель находится под действием силы, заставляющей его двигаться, и под действием пары сил, вызывающий его перекос в направляющих. Таким образом, в рассматриваемом случае на­блюдается аналогичное явление перекоса, с которым приходится считаться при исследовании механизма со стержневым толкателем. *С увеличением размеров кулачка плечо упомянутой пары сил

2.2 Синтез кулачковых механизмов Основные- задачи, решаемые при синтезе кулачковых механизмов

Синтез (проектирование) кулачковых механизмов по заданному закону движения толкателя.

Под синтезом кулачкового механизма будем понимать построение профиля кулачка, в каждой точке которого угол давления не превышал бы допустимого, а размеры самого профиля были бы минимальны.

Данная задача решается в 3 этапа:

1. Строится график заданного закона движения (как правило либо график ускорения точки В толкателя как функция угла положения – a_B = f(φ₁), либо график линейной скорости точки В – v_B= f(φ₁)). Требуется построить график перемещения точки В как функцию от угла поворота кулачка s_B= f(φ₁).

2. Определение минимального размера кулачковой шайбы при условии, что угол давления в любой точке профиля не превышает допустимого.

3. Построение профиля кулачка.

6.5.1 Построение закона движения оси толкателя.

Дано: Надо построить:

вид графика a_B = f(φ₁), 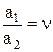графики a_B = f(φ₁)

максимальный ход v_B= f(φ₁)

толкателя h_т s_B= f(φ₁)

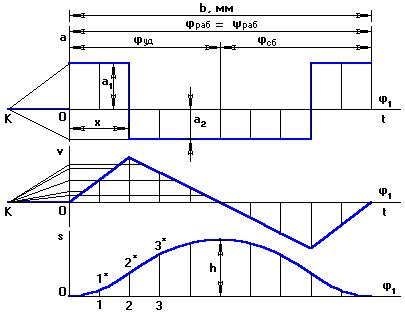b – база графика (сколько отводиться на график по оси φ_1­).

Порядок построения:

1. Произвольно выбирается база графика.

2. Считаем масштаб по оси φ₁:

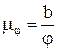, мм/град

3. Если задан симметричный вид графика, то:

φ_уд = φ_сб à b_уд = b_сб

В общем случае закон движения может быть несимметричным.

4. Зададимся произвольным образом а₁= 40 ÷ 50 мм. Тогда

а₂= а₁/ν

Возникает вопрос: каким должно быть расстояние х ?

Его находят из условия равенства площадей под и над осью φ₁.

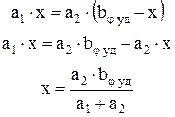
Почему надо выдерживать равенство площадей?

Физический смысл площади под кривой ускорения на площадке х – скорость толкателя на данном участке.

Физический смысл площади под кривой скорости на участке φ_уд – максимальное удаление (перемещение т.В толкателя). Если площади не будут равновеликими, то толкатель, поднявшись на одну величину, опустится на другую.

Построив график ускорения, строим график скорости методом графического интегрирования, выбрав отрезок интегрирования ОК₁. Интегрируя график скорости (с отрезком интегрирования ОК₂, обычно ОК₁=ОК₂), получаем график перемещения т.В толкателя. Полученную ломаную линию заменяют плавной кривой.

Расчет масштаба:

(уS_В)_max на графике перемещений получается автоматически, и его величина зависит от отрезка ОК₂. Тогда, зная ход толкателя, масштаб перемещения будет:

μ=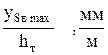

Затем в первом приближении принимаем, что кулачок вращается равномерно, тогда угол поворота кулачка пропорционален времени поворота, и оси φ и t совпадают, но каждая ось имеет свой масштаб.

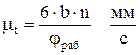
где b – в [мм]; частота вращения кулачка n – [об/мин]; φ_раб – [град].

Масштаб скорости:

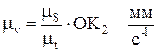
Масштаб ускорения:

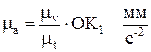
6.5.2 Определение минимального радиуса кулачковой шайбы по известному закону движения толкателя.

6.5.2 а) для кулачка с поступательно движущимся толкателем:

Дано: s_B=f(φ₁); v_B= f(φ₁); [θ]

Определить: r_{o min}

при условии, что угол давления в любой точке профиля кулачка не превышает допустимый.

Порядок построения графика кинематических отношений:

1. проводится вертикальная ось s_B,мм вдоль которой от произвольно выбранной точки В_о (начало отсчета) откладываются отрезки перемещения т.В, взятые с графика s_B=f(φ₁). Масштаб по оси μ_s* перемещений может быть равен масштабу графика перемещений μ_s.

2. 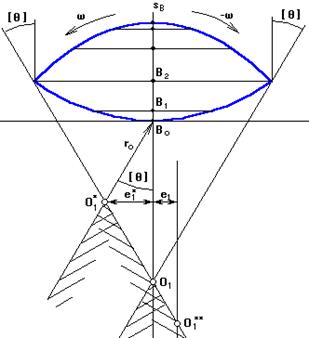в каждой из полученных точек определяют отрезки кинематических отношений, посчитанные в масштабе μ_s*, и откладывают их под углом в 90º по направлению вращения кулачка.

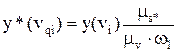мм

Там, где отрезок имеет максимальное значение, восстанавливается перпендикуляр, и под углом [θ] проводится луч.

3. Если учитывать реверс, то второй луч проводят под углом [θ] через отрезок кинематических отношений, отложенный под углом в 90º по направлению реверса и имеющий максимальное значение.

Если реверс не учитывать, второй луч проводят через т.Во под углом [θ]. Если допускается внеосность, то она будет равна е₁*. Если внеосность равна нулю, то центр кулачка будет в т.О₁:

r_o = O₁B_o

Если внеосность задана в техническом задании, например левая, то проводят прямую, параллельную прямой О₁В_о и отстоящая от нее на расстоянии, равном величине внеосности е₁, с учетом масштаба μ_s*. В итоге получают точку О₁**.

6.5.2 б) для кулачка с качающимся толкателем:

Порядок построения: В произвольном месте выбирается точка С_о, из которой радиусом, равным длине толкателя, проводят дугу окружности. По хордам откладывают перемещения т.В. Полученные точки последовательно соединяют с т.С_о.

1. На этих прямых и на их продолжении откладываются отрезки кинематических отношений, посчитанные в масштабе μ_s* по вышеприведенной формуле. Там, где отрезок имеет максимальное значение, восстанавливается перпендикуляр, и под углом [θ] проводится луч.

2. 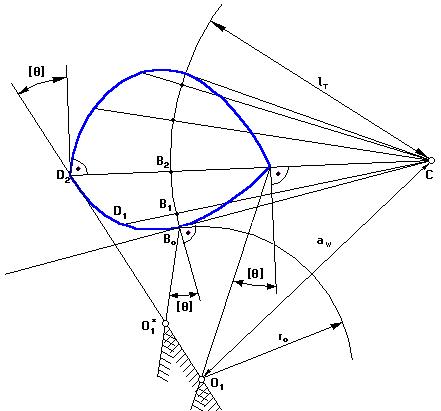Если учитывать реверс, то второй луч проводят под углом [θ] через отрезок кинематических отношений, отложенный под углом в 90º по направлению реверса и имеющий максимальное значение. Центр кулачка будет в т.О₁*:

r_o = O₁Bo

Если реверс не учитывать, то второй луч проводят через т.Во под углом [θ]. Центр кулачка будет в т.О₁*:

r_o = O₁*Bo

2.10 Выбор радиуса ролика

Выборрадиуса R_Р ролика.Радиус R_Р ролика в силовых механиз­мах назначают по условию контактной прочности, т. е. с учетом

2.11 Построение профиля кулачка.

а) с поступательно движущимся толкателем (рис. 6.5.3.а):

Дано:

r_{o min}, внеосность левая е, φ_раб = ψ_раб, ω_к=ω₁, s_B = f(φ₁)

Требуется построить профиль кулачка.

В обращенном движении кулачок вращается с угловой скоростью, раной: ω₁ + (–ω₁) = 0.

Порядок построения:

На окружности, радиусом r =r_o , проведенной в масштабе μ_l, с левой стороны от оси О₁ на расстоянии е выбирается точка В_о (пересечение оси толкателя, отстоящей на величину е от точки О₁, с окружностью r_{o min}). Точку В_о соединяют с центром О₁. От полученного луча В_оО₁ в направлении (–ω₁) откладывают угол φ_раб=ψ_раб и проводят луч О₁В₁₀. Полученная дуга В_оВ₁₀ делится на 10 равных частей. В каждой из позиций 1,2… проводится положение оси толкателя в обращенном движении, при этом ось толкателя, перемещаясь в направлении (–ω₁), будет все время касаться окружности радиуса е, проведенной из центра О₁ с учетом масштаба μ_l. В каждой из позиций от точек 1,2,3… откладывают перемещения т.В толкателя вдоль оси толкателя, взятые с графика перемещений с учетом соотношения масштабов μ_l и μ_s. Полученные точки 1*,2*,3*… соединяют плавной кривой и получают центровой или теоретический профиль. Для построения рабочего профиля необходимо знать радиус ролика толкателя. Если он не задан, то его выбирают из конструктивных соображений:

r_p= 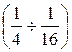r_{o min}

Кроме того, радиус ролика должен быть таким, чтобы при построении профиля кулачка не было заострения в вершине кулачка. Выбрав радиус ролика, из любых точек теоретического профиля кулачка (чем чаще, тем лучше) проводят дуги окружности r=r_p внутренним образом. Проведя огибающую к дугам, получают рабочий профиль кулачка. Если требуется построить профиль кулачка с поступательно движущимся толкателем и внеосностью е=0, то порядок построения профиля будет таким же, только ось толкателя будет проходить через центр вращения кулачка О₁.

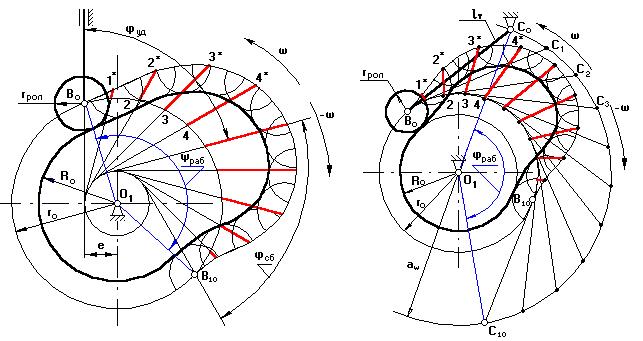
рис. 6.5.3.а рис. 6.5.3.б

б) с качающимся толкателем (рис. 6.5.3.б):

Дано:

r_{o min}, l_т, φ_раб = ψ_раб, ω_к=ω₁, s_B = f(φ₁), a_w (из чертежа для определения r_{o min})

Требуется построить профиль кулачка.

Порядок построения:

В масштабе μ_l проводятся окружности радиусами r_o и a_w. В произвольном месте окружности с r = a_w выберем т.С₀. Соединим точку С₀ с точкой О₁. От полученного луча в направлении (–ω₁) отложим угол φ_раб = ψ_раб, получим точку С₁₀. Дугу С₀С₁₀ разделим на 10 равных частей (получим точки С₁,С₂,С₃…– положение оси толкателя в обращенном движении). Из полученных точек проводим окружности радиусом l_т до пересечения с окружностью радиуса r_{o_min}. Из полученных точек 1,2,3… по хордам соответствующих дуг откладывают перемещения т.В толкателя, взятых с графика перемещения с учетом масштаба μ_l. Полученные точки 1*,2*,3*… соединяют плавной кривой – теоретический профиль кулачка. Радиусом ролика проводят дуги во внутрь и строят огибающую. Это и есть действительный профиль кулачка.

2.12 Определение координат профиля кулачка

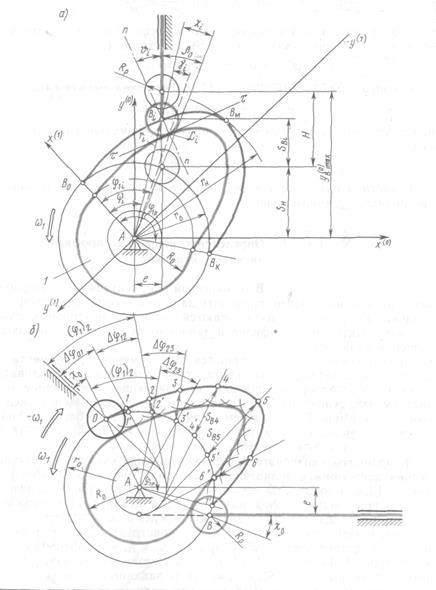
2.1 Назначение и виды зубчатых механизмов

Зубчатыми называются механизмы, составленные из зубчатых колёс и служащие для передачи вращательного движения от одного вала к другому при требуемом изменении угловой скорости и момента.

Зубчатые механизмы, служащие для уменьшения частоты вращения механизма называются редукторами, а для повышения – мультипликаторами.

Широкое применение нашли редукторы, так как двигатели делают обычно быстроходными, чтобы получить большую мощность, повысить КПД при малых и массе, а частота вращения вала рабочей машины обуславливается требованиями выправления технологического процесса и часто бывают значительно меньше частоты вращения вала двигателя.

Передаточное отношения.

Важнейшей характеристикой зубчатого механизма является передаточное отношение, под которым понимают отношение скоростей каких – либо двух звеньев

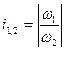
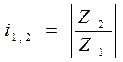Z – число зубьев

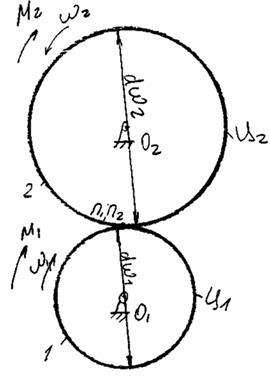
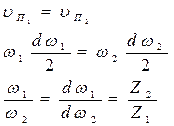
Диаметр начальной окружности соответствует числу зубьев

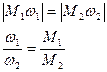
При // осях вращения можно говорить 0 «+» или «-» передаточном отношении. Передаточное отношение «+» если направления угловых скоростей совпадают, и «-» если направления угловых скоростей противоположны.

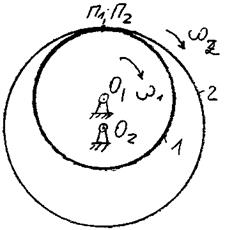
- передача с внутренним зацеплением

Для зубчатых механизмов состоящих из двух колёс применяют иногда характеристику, которая называется передаточным числом, под которым понимают отношение числа зубьёв к числу зубьев шестерни.

Под шестерней понимают колесо с меньшим числом зубьев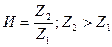

Для редукторов передаточное отношение совпадает с передаточным числом.

Различают: одноступенчатые механизмы и многоступенчатые.

Составленные из зубчатых колёс.

Одноступенчатые: называются простейшими механизмами, которые не могут быть расчленены на более простые механизмы.

Многоступенчатые: называют механизмы, образованные путём соединения нескольких одно ступенчатых механизмов, которые в данном случае называются ступенями.

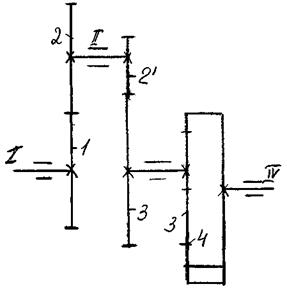Передаточное отношение многоступенчатого механизма равно произведения передаточного отношения его ступеней.

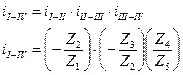
Многоступенчатые механизмы применяют для получения больших передаточных отношений.

В этих механизмах передаточное отношение первой ступени не превышает 6 в силовых передачах, и 10 -12 – в механизмов приборов.

2.2 СИНТЕЗ ЗУБЧАТЫХ МЕХАНИЗМОВ

Основные понятия.Механизмы с низшими парами (рычажные механизмы), синтез которых был рассмотрен в предыдущих пара­графах, обеспечивают передачу значительных сил, так как звенья пары соприкасаются по поверхности. Но условие постоянного со­прикасания по поверхности ограничивает число возможных видов низших пар. В механизмах применяется всего шесть видов низших пар: враща^ тельная, поступательная, винтовая, ци­линдрическая, сферическая и плоскостная. Поэтому многие практически важные за­коны преобразования движения звеньев не могут быть получены посредством ме­ханизмов, имеющих только низшие пары. Значительно большие возможности для воспроизведения почти любого закона движения имеют механизмы, содержащие высшие пары, так как условия касания взаимодействующих поверхностей звень­ев высшей пары по линиям и точкам мо­гут быть выполнены для бесчисленного множества различных поверхностей.

Взаимодействующие поверхности звеньев высшей пары, обеспе­чивающие заданный закон их относительного движения, называ­ются сопряженными ловерхностями. При воспроизве­дении возвратного движения можно иметь одну пару сопряженных поверхностей (например, в кулачковых механизмах). Если же тре­буется воспроизвести непрерывное движение в одном направлении, то надо иметь несколько последовательно взаимодействующих пар сопряженных поверхностей, которые располагаются на выступах, называемых зубьями.

Высшая кинематическая пара, образуемая последовательно взаимодействующими поверхностями зубьев, называется зубча­тым зацеплением. Термин «зацепление» (без прибавления слова «зубчатое») можно отнести и к одной паре сопряженных по­верхностей. Тогда он является синонимом термина «высшая пара». Основная теорема зацепления.Синтез зацепления состоит в отыскании сопряженных поверхностей по заданному закону их от­носительного движения. Для решения этой задачи используется ос­новная теорема зацепления, устанавливающая связь между геомет­рией сопряженных поверхностей и заданным законом их относительного движения.

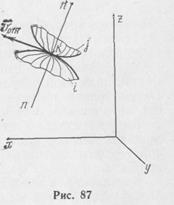
Обозначим через г7_ОТн вектор скорости точки контакта К сопря­женных поверхностей (рис. 87) в движении звена I относительно звена / (или наоборот). Для данной точки К эта скорость одно-