Теплоотдача в дисперсных системах с твердой фазой

Теплоотдача в дисперсных системах с твердой фазой в химической технологии имеет большое практическое значение, особенно при теплообмене между движущимся теплоносителем и неподвижным слоем зернистого материала (насадки), а также теплоносителем и псевдоожиженным или кипящим слоем. Такой вид теплообмена сопровождает многие контактно-каталитические и массообменные процессы.

Теплообмен при движении теплоносителя через неподвижный слой зернистого материала или насадки зависит от формы и размера зерен (элементов насадки), материала насадки, прозрачности слоя, физических свойств теплоносителя, температур теплоносителя и твердой фазы и т.д.

Коэффициенты теплоотдачи от газа к неподвижным частицам зернистого материала (насадки) могут быть рассчитаны по критериальным уравнениям:

при 40 < Re < 200

Nu= 0,1 Re; (7.122)

при 200 < Re < 610

Nu = 0,286 Re^0,8, (7.123)

где 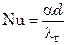; 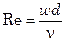( 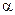– коэффициент теплоотдачи от газа к неподвижным частицам или насадке; 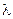_г – коэффициент теплопроводности газа; d – диаметр зерна или насадочного тела; w – скорость газа, отнесенная к полному сечению аппарата).

Для расчета коэффициента теплоотдачи при движении газа через неподвижную насадку с малой теплопроводностью [ 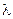= 0,13÷1,7 Вт/м·К] в области Re = 50–2000 рекомендуется эмпирическое уравнение

Nu = 0,123Re^0,83, (7.124)

где 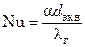; 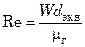(d_экв – эквивалентный диаметр насадки; W = wρ_г – массовая скорость газа).

Аналогично для насадки с высокой теплопроводностью [ 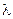= 37÷383 Вт/м·К] в области Re = 50–1770 расчетное уравнение имеет вид

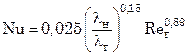, (7.125)

где 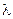_н – теплопроводность насадки.

Теплоотдача от псевдоожиженного слоя к поверхности теплообмена (или в обратном направлении) относится к наиболее интенсивному виду теплообмена с зернистыми материалами. Коэффициент теплоотдачи для этого случая теплообмена зависит от свойств зернистого материала, физических свойств и скорости ожижающего агента, а также от расположения и конструкции поверхности теплообмена (поверхности стенок аппарата, труб или других теплообменных элементов, помещенных внутри слоя).

При возрастании скорости ожижающего агента коэффициент теплоотдачи увеличивается, достигает своего максимального значения 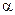_max, после чего обычно уменьшается, что объясняется возрастающим противоположным действием на теплообмен интенсивности движения частиц около поверхности теплообмена и увеличением порозности слоя ε. Очевидно, что наиболее эффективный теплообмен достигается при максимальных значениях коэффициента теплоотдачи, которым соответствует оптимальная скорость w_опт:

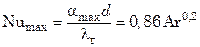. (7.126)

При этом .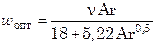

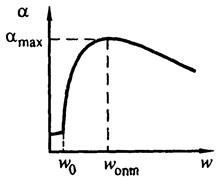Рисунок 7.15 – Изменение коэффициента теплоотдачи от поверхности к псевдоожиженному слою с изменением скорости газа

В диапазоне от скорости начала псевдоожижения до w_опт величина 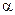резко возрастает по очень сложной закономерности (рис. 7.15), которую со значительным запасом можно принять линейной. За пределами w_опт величина 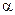на некотором участке остается неизменной, после чего монотонно падает.

Коэффициент теплоотдачи от несущей газовой среды к твердым частицам в потоке газовзвеси может быть рассчитан по следующим формулам:

В области изменений j = 1¸5; (r_т/r_г) < 1100;

при 30 < Re_г < 480

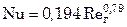; (7.127)

при 480 < Re_г < 2000

;

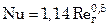в случае 5 < φ <30;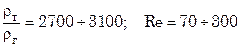

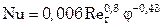. (7.128)

В формулах (7.127) и (7.128) φ – относительная массовая концентрация твердых частиц в потоке газовзвеси, кг/кг; ρ_т – плотность твердых частиц. В качестве определяющего линейного размера принят размер твердых частиц.

Теплоотдача от газового потока к внутренней поверхности труб, заполненных твердыми частицами, описывается критериальным уравнением

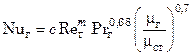; (7.129)

при Re_г < 40 с = 1,18·10^–3; т = 1,5;

при 40 < Re_г < 1200 с = 3,35·10^-3; т = 1,2;

при Re_г > 1200 с = 2,95·10^–2; т = 0,9.

Теплоотдача от жидкостного потока к внутренней поверхности труб, заполненных твердыми частицами:

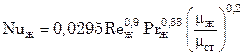. (7.130)

Сложная теплоотдача

Разделение общего процесса переноса тепла на элементарные – теплопроводность, конвекцию и тепловое излучение – является лишь методическим приемом. В действительности эти явления протекают одновременно и, естественно, влияют друг на друга. Конвекция, например, всегда сопровождается теплопроводностью или лучеиспусканием; теплопроводность в пористых телах – конвекцией и лучеиспусканием в порах, а лучеиспускание – теплопроводностью и конвекцией.

В практических расчетах разделение таких сложных процессов на элементарные не всегда возможно и целесообразно. Обычно результат одновременного действия отдельных элементарных процессов приписывают одному из них, которое принимают главным. Влияние же остальных сказывается лишь на величине количественной характеристики основного.

Если теплообмен происходит между твердой стенкой и газообразной средой (например, воздухом), то тепло передается совместно конвекцией и излучением. Такой процесс переноса тепла получил название сложной теплоотдачи. Типичным примером сложной теплоотдачи являются потери тепла стенками аппаратов в окружающую среду.

Количество тепла, отдаваемое стенкой в единицу времени омывающему ее газу, за счет конвективного теплообмена составит 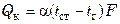, а за счет теплового излучения

.

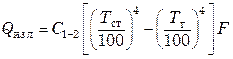Если ввести обозначения

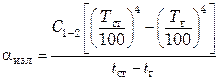, (7.131)

где 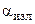– коэффициент теплоотдачи при лучеиспускании, то количество тепла, переданное излучением, выразится равенством

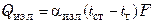. (7.132)

Общее количество тепла, отданное стенкой в единицу времени, составит:

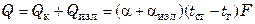, (7.133)

либо

,

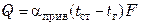где 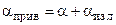– приведенный коэффициент теплоотдачи, показывающий, какое количество тепла отдает 1 м² стенки в окружающую среду в единицу времени при разности температур стенки и среды 1 °С за счет конвективного теплообмена и теплового излучения.

В инженерных расчетах 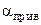часто определяют приближенно по эмпирическим уравнениям. Например, при расчете тепла, теряемого наружной поверхностью аппаратов, находящихся в закрытых помещениях, в окружающую среду, 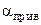можно рассчитать, пользуясь уравнением

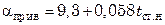, (7.134)

где 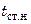– температура наружной поверхности стенки аппарата. Это уравнение применимо в пределах изменения 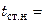50¸350 °С.

Для уменьшения потерь тепла в окружающую среду аппараты и трубопроводы покрывают слоем тепловой изоляции.