Тригонометрические функции.
Функция 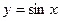 . Область определения функции – вся числовая прямая,
. Область определения функции – вся числовая прямая, 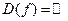 . Она принимает значения, удовлетворяющие условию
. Она принимает значения, удовлетворяющие условию 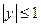 , то есть
, то есть 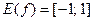 . Функция ограничена и сверху и снизу. Наименьшее значение
. Функция ограничена и сверху и снизу. Наименьшее значение 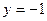 функция принимает в точках
функция принимает в точках 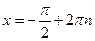 (
( 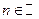 ), и эти точки являются точками минимума. Наибольшее значение
), и эти точки являются точками минимума. Наибольшее значение 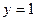 функция принимает в точках
функция принимает в точках 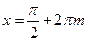 (
( 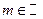 ), и эти точки являются точками максимума. График функции
), и эти точки являются точками максимума. График функции 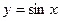 пересекает ось абсцисс в точках
пересекает ось абсцисс в точках 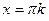 (
( 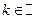 ). Функция
). Функция 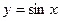 является периоди
является периоди 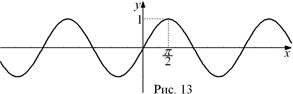 ческой, ее период
ческой, ее период 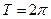 . Функция
. Функция 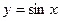 является нечетной, ее график симметричен относительно начала координат. Функция не является монотонной на всей области определения, но она возрастает на каждом промежутке
является нечетной, ее график симметричен относительно начала координат. Функция не является монотонной на всей области определения, но она возрастает на каждом промежутке 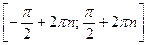 (
( 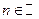 ) и убывает на каждом промежутке
) и убывает на каждом промежутке 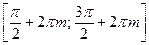 (
( 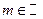 ). График этой функции называется синусоидой. Учитывая периодичность, достаточно построить график на отрезке длиной
). График этой функции называется синусоидой. Учитывая периодичность, достаточно построить график на отрезке длиной 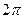 , например
, например 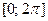 , а затем копировать его (рис. 13).
, а затем копировать его (рис. 13).
Функция 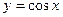 . Область определения функции вся числовая прямая:
. Область определения функции вся числовая прямая: 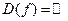 . Она принимает значения, удовлетворяющие условию
. Она принимает значения, удовлетворяющие условию 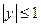 , то есть
, то есть 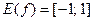 . Функция ограничена и сверху и снизу. Наименьшее значение
. Функция ограничена и сверху и снизу. Наименьшее значение 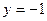 функция принимает в точках
функция принимает в точках 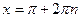 (
( 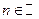 ), и эти точки являются точками минимума. Наибольшее значение
), и эти точки являются точками минимума. Наибольшее значение 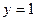 функция принимает в точках
функция принимает в точках 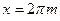 (
( 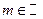 ), и эти точки являются точками максимума. График функции
), и эти точки являются точками максимума. График функции 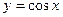 пересекает ось абсцисс в точках
пересекает ось абсцисс в точках 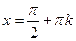 (
( 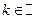 ). Функция
). Функция 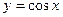 является периодической, ее период
является периодической, ее период 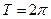 . Функция
. Функция 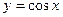 является четной, ее график симметричен относительно оси ординат. Функция не является монотонной на всей области определения, но она возрастает на каждом промежутке
является четной, ее график симметричен относительно оси ординат. Функция не является монотонной на всей области определения, но она возрастает на каждом промежутке 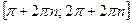 (
( 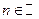 ) и убывает на каждом промежутке
) и убывает на каждом промежутке 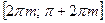 (
( 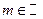 ). График этой функции называется косинусоидой. Учитывая
). График этой функции называется косинусоидой. Учитывая 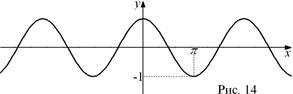 периодичность, достаточно построить график на отрезке длиной
периодичность, достаточно построить график на отрезке длиной 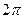 , например
, например 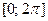 , а затем копировать его (рис. 14).
, а затем копировать его (рис. 14).
Функция 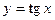 . Область определения функции все действительные значения х, кроме
. Область определения функции все действительные значения х, кроме 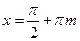 (
( 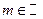 ):
): 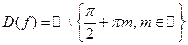 . Множество ее изменения – вся числовая прямая,
. Множество ее изменения – вся числовая прямая, 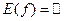 . Функция
. Функция 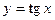 не ограничена ни сверху, ни снизу. Она не имеет точек экстремума и не принимает ни наименьшее, ни наибольшее значения. График функции
не ограничена ни сверху, ни снизу. Она не имеет точек экстремума и не принимает ни наименьшее, ни наибольшее значения. График функции 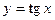 пересекает ось абсцисс в точках
пересекает ось абсцисс в точках 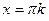 (
( 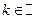 ).
).  Функция
Функция 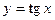 является периодической, ее период
является периодической, ее период 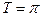 . Функция
. Функция 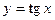 является нечетной, ее график симметричен относительно начала координат. Функция не является монотонной на всей области определения, но она возрастает на каждом промежутке
является нечетной, ее график симметричен относительно начала координат. Функция не является монотонной на всей области определения, но она возрастает на каждом промежутке 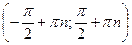 (
( 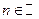 ), в точках
), в точках 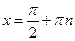 (
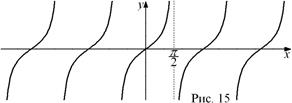
( 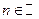 ) функция имеет разрывы. График этой функции называется тангенсоидой. Учитывая периодичность, достаточно построить график на отрезке длиной
) функция имеет разрывы. График этой функции называется тангенсоидой. Учитывая периодичность, достаточно построить график на отрезке длиной 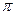 , например
, например 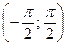 , а затем копировать его (рис. 15).
, а затем копировать его (рис. 15).
Функция 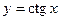 . Область определения функции все действительные значения х, кроме
. Область определения функции все действительные значения х, кроме 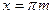 (
( 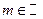 ):
): 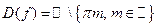 . Множество ее изменения – вся числовая прямая,
. Множество ее изменения – вся числовая прямая, 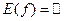 . Функция
. Функция 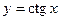 не ограничена ни сверху, ни снизу. Она не имеет точек экстремума и не принимает ни наименьшее, ни наибольшее значения. График функции
не ограничена ни сверху, ни снизу. Она не имеет точек экстремума и не принимает ни наименьшее, ни наибольшее значения. График функции 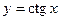 пересекает ось абсцисс в точках
пересекает ось абсцисс в точках 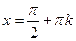 (
( 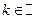 ). Функция
). Функция 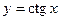 является периодической, ее период
является периодической, ее период 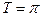 . Функция
. Функция 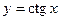 является нечетной, ее график симметричен относительно начала координат. Функция не является монотонной на всей области определения, но она убывает на каждом промежутке
является нечетной, ее график симметричен относительно начала координат. Функция не является монотонной на всей области определения, но она убывает на каждом промежутке 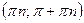 (
( 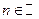 ), в точках
), в точках 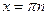 (
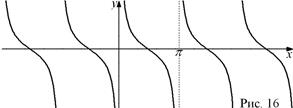
( 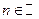 ) функция имеет разрывы. График этой функции называется котангенсоидой. Учитывая периодичность, достаточно построить график на отрезке длиной
) функция имеет разрывы. График этой функции называется котангенсоидой. Учитывая периодичность, достаточно построить график на отрезке длиной 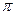 , например
, например 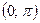 , а затем копировать его (рис. 16).
, а затем копировать его (рис. 16).
 Обратные тригонометрические функции.
Обратные тригонометрические функции.
 Напомним определения обратных тригонометрических выражений. Арксинусом числа а называется угол a такой, что
Напомним определения обратных тригонометрических выражений. Арксинусом числа а называется угол a такой, что 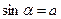 и
и 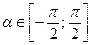 . Арккосинусом числа а называется угол a такой, что
. Арккосинусом числа а называется угол a такой, что 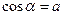 и
и 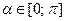 . Арктангенсом числа а называется угол a такой, что
. Арктангенсом числа а называется угол a такой, что 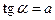 и
и 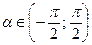 . Арккотангенсом числа а называется угол a, такой, что
. Арккотангенсом числа а называется угол a, такой, что 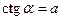 и
и 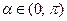 .
.
Функция 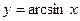 является обратной к функции
является обратной к функции 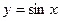 . Используя свойства прямой функции, получим свойства обратной. Для этого рассмотрим часть графика функции
. Используя свойства прямой функции, получим свойства обратной. Для этого рассмотрим часть графика функции 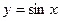 , на которой синус каждое свое значение принимает только один раз (промежуток монотонности функции) – отрезок
, на которой синус каждое свое значение принимает только один раз (промежуток монотонности функции) – отрезок 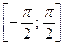 . Функция
. Функция 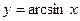 каждому значению синуса ставит в соответствие его аргумент. Таким образом, область определения функции
каждому значению синуса ставит в соответствие его аргумент. Таким образом, область определения функции 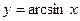 – отрезок [–1; 1], множество изменения – отрезок
– отрезок [–1; 1], множество изменения – отрезок 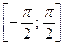 . Функция ограничена и сверху и снизу. Наименьшее значение
. Функция ограничена и сверху и снизу. Наименьшее значение 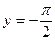 функция принимает в точке
функция принимает в точке 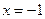 , наибольшее значение
, наибольшее значение 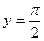 функция принимает в точке
функция принимает в точке 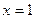 . Функция
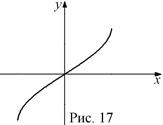
. Функция 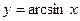 является нечетной, ее график симметричен относительно начала координат. Функция является монотонно возрастающей на всей области определения. График функции
является нечетной, ее график симметричен относительно начала координат. Функция является монотонно возрастающей на всей области определения. График функции 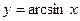 симметричен рассмотренной выше части графика функции
симметричен рассмотренной выше части графика функции 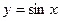 относительно биссектрисы первой и третьей координатных четвертей (рис. 17).
относительно биссектрисы первой и третьей координатных четвертей (рис. 17).
 Функция
Функция 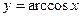 является обратной к функции
является обратной к функции 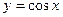 . Используя свойства прямой функции, получим свойства обратной. Для этого рассмотрим часть графика функции
. Используя свойства прямой функции, получим свойства обратной. Для этого рассмотрим часть графика функции 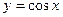 , на которой косинус каждое свое значение принимает только один раз (промежуток монотонности функции) – отрезок
, на которой косинус каждое свое значение принимает только один раз (промежуток монотонности функции) – отрезок 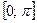 . Функция
. Функция 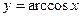 каждому значению косинуса ставит в соответствие его аргумент. Таким образом, область определения функции
каждому значению косинуса ставит в соответствие его аргумент. Таким образом, область определения функции 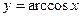 – отрезок [–1; 1], множество изменения – отрезок
– отрезок [–1; 1], множество изменения – отрезок 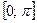 . Функция ограничена и сверху и снизу. Наименьшее значение
. Функция ограничена и сверху и снизу. Наименьшее значение 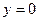 функция принимает в точке
функция принимает в точке 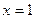 , наибольшее значение
, наибольшее значение 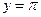 функция принимает в точке
функция принимает в точке 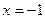 . Функция
. Функция 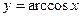 не является ни четной, ни нечетной. Функция является монотонно убывающей на всей области определения. График функции
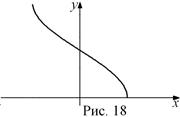
не является ни четной, ни нечетной. Функция является монотонно убывающей на всей области определения. График функции 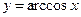 симметричен рассмотренной выше части графика функции
симметричен рассмотренной выше части графика функции 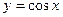 относительно биссектрисы первой и третьей координатных четвертей (рис. 18).
относительно биссектрисы первой и третьей координатных четвертей (рис. 18).
 Функция
Функция 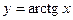 является обратной к функции
является обратной к функции 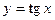 . Используя свойства прямой функции, получим свойства обратной. Для этого рассмотрим одну ветвь графика функции
. Используя свойства прямой функции, получим свойства обратной. Для этого рассмотрим одну ветвь графика функции 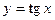 , на которой тангенс каждое свое значение принимает только один раз (промежуток монотонности функции) – интервал
, на которой тангенс каждое свое значение принимает только один раз (промежуток монотонности функции) – интервал 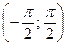 . Функция
. Функция 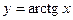 каждому значению тангенса ставит в соответствие его аргумент. Таким образом, область определения функции
каждому значению тангенса ставит в соответствие его аргумент. Таким образом, область определения функции 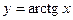 – вся числовая прямая,
– вся числовая прямая, 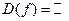 , множество изменения – интервал
, множество изменения – интервал 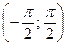 . Функция ограничена и сверху и снизу, но она не принимает ни наименьшего, ни наибольшего значений. Функция
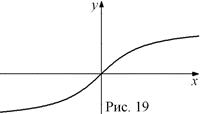
. Функция ограничена и сверху и снизу, но она не принимает ни наименьшего, ни наибольшего значений. Функция 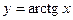 является нечетной, ее график симметричен относительно начала координат. Функция является монотонно возрастающей на всей области определения. График функции
является нечетной, ее график симметричен относительно начала координат. Функция является монотонно возрастающей на всей области определения. График функции 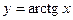 симметричен ветви графика функции
симметричен ветви графика функции 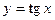 относительно биссектрисы первой и третьей координатных четвертей (рис. 19).
относительно биссектрисы первой и третьей координатных четвертей (рис. 19).
 Функция
Функция 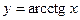 является обратной к функции
является обратной к функции 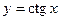 . Используя свойства прямой функции, получим свойства обратной. Для этого рассмотрим одну ветвь графика функции
. Используя свойства прямой функции, получим свойства обратной. Для этого рассмотрим одну ветвь графика функции 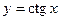 , на которой котангенс каждое свое значение принимает только один раз (промежуток монотонности функции) – интервал
, на которой котангенс каждое свое значение принимает только один раз (промежуток монотонности функции) – интервал 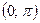 . Функция
. Функция 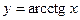 каждому значению котангенса ставит в соответствие его аргумент. Таким образом, область определения функции
каждому значению котангенса ставит в соответствие его аргумент. Таким образом, область определения функции 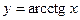 – вся числовая прямая,
– вся числовая прямая, 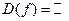 , множество изменения – интервал
, множество изменения – интервал 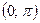 . Функция ограничена и сверху и снизу, но она не принимает ни наименьшего, ни наибольшего значений. Функция
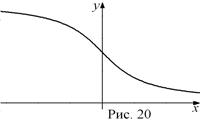
. Функция ограничена и сверху и снизу, но она не принимает ни наименьшего, ни наибольшего значений. Функция 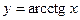 не является ни четной, ни нечетной. Функция является монотонно убывающей на всей области определения. График функции
не является ни четной, ни нечетной. Функция является монотонно убывающей на всей области определения. График функции 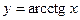 симметричен ветви графика функции
симметричен ветви графика функции 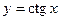 относительно биссектрисы первой и третьей координатных четвертей (рис. 20).
относительно биссектрисы первой и третьей координатных четвертей (рис. 20).
 Показательная функция
Показательная функция 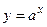 , где
, где 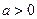 и
и 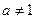 . Область определения функции – вся числовая прямая,
. Область определения функции – вся числовая прямая, 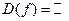 . Функция принимает только положительные значения:
. Функция принимает только положительные значения: 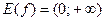 . Функция ограничена снизу и не ограничена сверху. Она не принимает ни наименьшего, ни наибольшего значений, не имеет точек экстремума. Показательная функция не является ни четной, ни нечетной. График функции пересекает ось ординат в точке
. Функция ограничена снизу и не ограничена сверху. Она не принимает ни наименьшего, ни наибольшего значений, не имеет точек экстремума. Показательная функция не является ни четной, ни нечетной. График функции пересекает ось ординат в точке 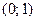 , ось абсцисс он не пересекает. При
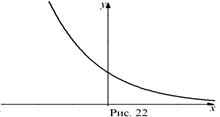
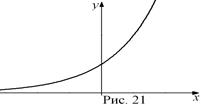
, ось абсцисс он не пересекает. При 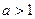 функция является возрастающей (рис. 21), а при
функция является возрастающей (рис. 21), а при 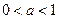 – убывающей (рис. 22) на всей области определения.
– убывающей (рис. 22) на всей области определения.
Логарифмическая функция 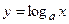 , где
, где 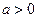 и
и 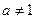 . Логарифмическая функция является обратной к показательной. Поэтому ее область определения – множество положительных чисел,
. Логарифмическая функция является обратной к показательной. Поэтому ее область определения – множество положительных чисел, 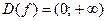 , область изменения – множество действительных чисел,
, область изменения – множество действительных чисел, 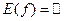 . Функция не
. Функция не 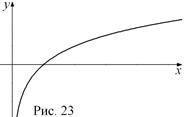 ограничена ни сверху, ни снизу. Она не принимает ни наименьшего, ни наибольшего значений, не имеет точек экстремума. Логарифмическая функция не является ни четной, ни нечетной. График функции пересекает ось абсцисс в точке
ограничена ни сверху, ни снизу. Она не принимает ни наименьшего, ни наибольшего значений, не имеет точек экстремума. Логарифмическая функция не является ни четной, ни нечетной. График функции пересекает ось абсцисс в точке 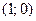 , ось ординат график не пересекает. При
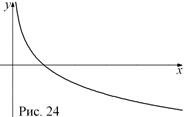
, ось ординат график не пересекает. При 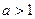 функция является возрастающей (рис. 23), а при
функция является возрастающей (рис. 23), а при 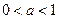 – убывающей (рис. 24) на всей области определения. График функции
– убывающей (рис. 24) на всей области определения. График функции 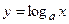 симметричен графику функции
симметричен графику функции 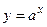 относительно биссектрисы первой и третьей координатных четвертей.
относительно биссектрисы первой и третьей координатных четвертей.
Упражнения
1. Найдите области определения функций:
а) 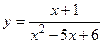 ; б)
; б) 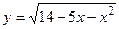 ;
;
в) 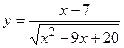 ; г)
; г) 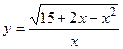 ;
;
д) 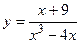 ; е)
; е) 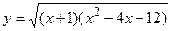 ;
;
ж) 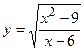 ; з)
; з) 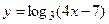 ;
;
и) 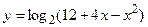 ; к)
; к) 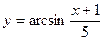 .
.
2. Найдите множества изменения функций:
а) 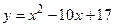 ; б)
; б) 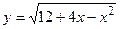 ;
;
в) 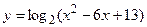 ; г)
; г) 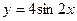 ;
;
д) 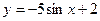 ; е)
; е) 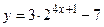 .
.
3. Докажите, что функции 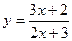 и
и 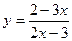 являются взаимно обратными.
являются взаимно обратными.
4. Какие из данных функций будут четными, какие нечетными:
а) 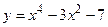 ; б)
; б) 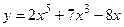 ;
;
в) 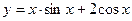 ; г)
; г) 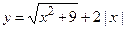 ;
;
д) 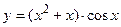 ; е)
; е) 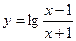 .
.
5. Определите, какие функции будут периодическими и найдите их периоды:
а) 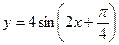 ; б)
; б) 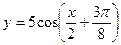 ;
;
в) 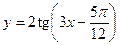 ; г)
; г) 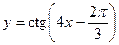 .
.
6. Представьте сложную функцию в виде цепочки элементарных функций:
а) 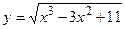 ; б)
; б) 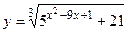 ;
;
в) 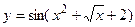 ; г)
; г) 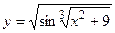 ;
;
д) 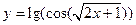 ; е)
; е) 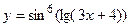 .
.
7. Составьте суперпозиции 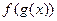 и
и 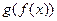 , если:
, если:
а) 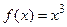 ,
, 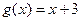 ; б)
; б) 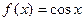 ,
, 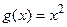 ;
;
в) 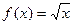 ,
, 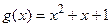 ;
;
г) 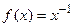 ,
, 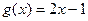 .
.
