Метод комплексных амплитуд
Переменный ток, напряжения. Периодические токи и напряжения. Мгновенные значения тока, напряжения и э.д.с. наибольшее распространение в электрических цепях получили синусоидальное или гармонические токи и напряжения. Ток изменяющийся по закону синуса называется синусоидальным или гармоническим. Мгновенное значение синусоидального тока, напряжения,э.д.с.
I= 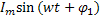 u=
u= 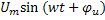 e=
e= 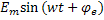 где:
где: 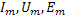 , максимальное значение или амплитуда тока, напряжения, э.д.с.
, максимальное значение или амплитуда тока, напряжения, э.д.с.
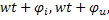
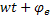 - фаза тока, напряжения, э.д.с.
- фаза тока, напряжения, э.д.с. 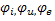 -начальная фаза тока, напряжения, э.д.с.
-начальная фаза тока, напряжения, э.д.с. 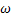 - угловая частота.
- угловая частота.
Период Т, частота f связаны соотношением: 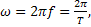 f=
f=  .
.
Важными параметрами синусоидальных колебаний являются действующее и среднее значения. Действующим значением тока I называется среднеквадратичное значение электрического токе зе период:
I= 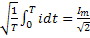 . Аналогично для напряжения и э.д.с.: U=
. Аналогично для напряжения и э.д.с.: U= 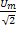 E=
E= 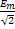 .
.
Среднее значение гармонического тока за период равен нулю, поэтому пользуется понятием среднего полупериодного значения, соответствующего только положительной полуволне:
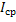 =
= 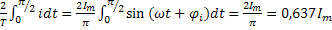 .
.
Генератор переменной э.д.с. устройство и принцип действия.
Синусоидальные колебания (токи, напряжения, э.д.с) можно представить различными способами: функциями времени (временные диаграммы ) в t-области, векторами, комплексными часами. Расчет электрических цепей синусоидальными источниками энергии облегчается, если синусоидально изменяющиеся токи, напряжения, э.д.с. изображать векторами или комплексными числами. Эти представления лежат в основе символического метода расчета электрических цепей- метода комплексных амплитуд. Векторное представление синусоидальных функции основано на том, что вектор каждой синусоидальной функции в соответствии ставится вращающийся вектор на комплексной плоскости. Этот вектор на комплексной плоскости является геометрическим изображением комплексного числа. Поэтому синусоидальным функциям соответствуют комплексные числа.
Мгновенному значению напряжения u= 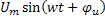 в любой момент времени соответствует комплексное число, которое называется комплексным мгновенным напряжением.
в любой момент времени соответствует комплексное число, которое называется комплексным мгновенным напряжением.
Оно изображается вектором на комплексной плоскости, длина которого равна амплитуде 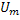 и который образует с вещественной осью угол
и который образует с вещественной осью угол 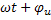
u= 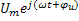 =
= 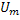 cos(
cos( 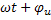 )+j
)+j 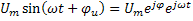 =
= 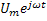 .
.
В начальной момент времени t=0, получается начальное положение вектора. Вектор образует с вещественной осью угол 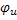 . такой вектор обозначается
. такой вектор обозначается
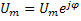 и называется комплексной амплитудой. Модулем комплексной амплитуды является вещественная амплитуда синусоидального напряжения, а аргументом – начальная фаза, т.е комплексная амплитуда включает оба параметра синусоиды: амплитуду и фазу. Это очень важное свойство комплексной амплитуды. Из приведенных выражений следует, что напряжение u=
и называется комплексной амплитудой. Модулем комплексной амплитуды является вещественная амплитуда синусоидального напряжения, а аргументом – начальная фаза, т.е комплексная амплитуда включает оба параметра синусоиды: амплитуду и фазу. Это очень важное свойство комплексной амплитуды. Из приведенных выражений следует, что напряжение u= 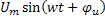 можно рассматривать как проекцию вращающегося вектора
можно рассматривать как проекцию вращающегося вектора 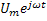 на ось мнимых чисел u=
на ось мнимых чисел u= 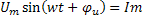 [
[ 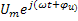 ]=Im[
]=Im[ 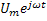 ], а напряжение u=
], а напряжение u= 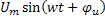 как проекцию вектора
как проекцию вектора 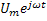 на ось вещественных чисел u=
на ось вещественных чисел u= 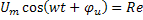 [
[ 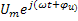 ]=Re[
]=Re[ 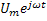 ].
].
Вместо комплексных амплитуд часто рассматривают комплексные действующие величины: U= 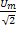 E=
E= 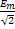 I=
I= 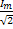 .
.
Переход от синусоидальных функций к комплексным действующим значениям позволяет упростить действия с синусоидальным функциями: сложение и вычитание, дифференцирование и интегрирование 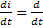 (
( 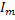
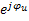 =j
=j 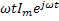
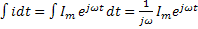 дифференцирование соответствует умножению на j
дифференцирование соответствует умножению на j 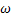 , а операция интегрирования соответствует делению на j
, а операция интегрирования соответствует делению на j 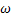 .
.
U=U 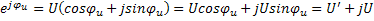 ”
”
U=U 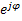 показательная форма комплекса
показательная форма комплекса
U’+jU” алг j 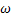 ебраическая форма комплекса напряжения.
ебраическая форма комплекса напряжения.
Используя формулу Эйлера, можно перейти в алгебраическая форму комплекса напряжения. Переход из алгебраической формы в показательную форму:
U=U’+jU”=U 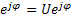
U= 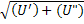 2
2 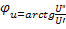
Умножение вектора наj и на-j . пусть имеется вектор U. Умножение его на j дает вектор, по модулю равный U, но повернутый по отношению к исходному вектору на угол 900 в сторону опережения(против часовой стрелки). Умножение вектора U на -j поворачивает вектор U на угол 900 в сторону отставания (по часовой стрелки).
Сложение гармонических функций. При анализе электрических цепей синусоидального тока приходится сталкиваться с суммированием синусоидальных функций времени с одинаковой частотой, но с различными начальными фазами. Непосредственное сложение в t – области связано с большими трудностями тригонометрического характера. Значительно проще задача решается графически при помощи векторной диаграммы или аналитический – путем суммирования комплексных чисел.
Вопросы для самоконтроля:
1. параметры синусоидального напряжения?
2.преимущество синусоидального напряжения?
3.как можно представить синусоидальную функцию времени?
4. записать показательную форму комплексной амплитуды ток?
5.найти графически сумму двух синусоидальных токов. Определить действующее значение и начальную фазу?
