Гармонические колебания и метод комплексных амплитуд

12.1. Представление о гармонических колебаниях.Если некоторая величина u(t) изменяется во времени по закону

u(t) = u_mcos(ωt + φ), (12.1)

то говорят, что происходят гармонические колебания,причем и_т называется амплитудой,ω - круговой частотой,а аргумент косинуса ωt + φ - фазойколебаний (полной фазой); последняя, если это требуется, приводится к значению, лежащему в пределах 0 ÷ 2π; или –π ÷ π; величину φ называют начальной фазой (а также фазовым сдвигом или просто фазой). Наименьший отрезок времени Т, обладающий тем свойством, что для любого момента t

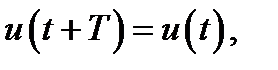
есть, по определению, период колебаний, а число периодов в секунду - частота, обозначаемая f. Очевидно

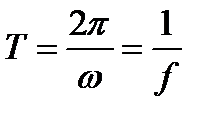(12.2)

В теории электромагнетизма встречаются, в частности, скалярные функции координат и времени вида

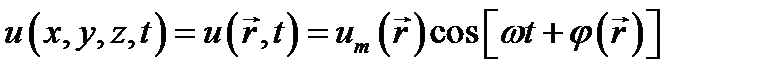, (12.3)

описывающие гармонические колебания в пространстве с амплитудами и фазами, которые могут изменяться от точки к точке. Три такие скалярные функции иногда являются компонентами вектора в декартовой или иной системе координат. Запишем выражение такого вектора в виде:

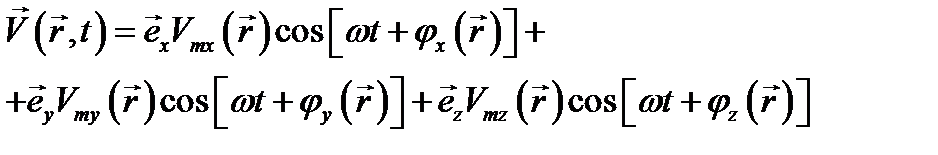(12.4)

В частности, если 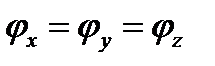т. е., как говорят, все компоненты вектора колеблются «в одной фазе», то

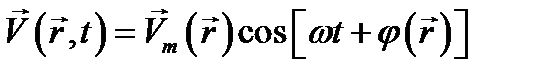, (12.4а)

где

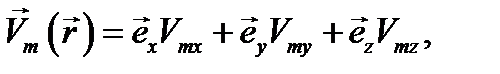
то есть амплитуда колеблющегося вектора. В дальнейшем при записи выражений типа (12.3), (12.4) мы большей частью будем для краткости опускать аргументы 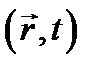и .

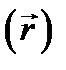12.2. Метод комплексных амплитуд. Перейдём к изложению обычно используемого в случае гармонических колебаний метода комплексных амплитуд. На основании известной формулы Эйлера функцию и (12.3) можно представить как вещественную часть экспоненциальной:

,

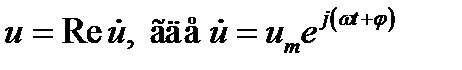или

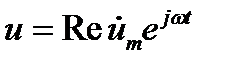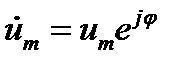, (12.5)

где множитель и_т называется комплексной амплитудой колебаний. Как видно, в комплексном представлении 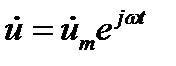мы имеем произведение функции координат 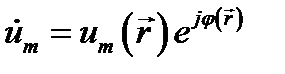и функции времени 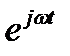. Совершенно аналогично

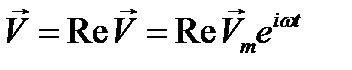, (12.6)

где комплексная амплитуда (функция координат) 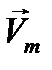есть

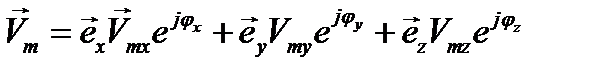, (12.7)

как это следует из (12.4), а в частном случае (12.4 а)

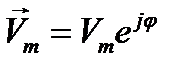. (12.7a)

Комплексная амплитуда несёт информацию как об амплитуде, так и о начальной фазе колебаний (трёх начальных фазах в общем случае вектора).

Пусть имеется линейное уравнение

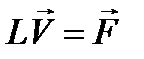, (12.8)

где 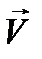неизвестная векторная функция вида (12.4), L - некоторый линейный (§ 7 п. 3) вещественный дифференциальный или интегральный оператор, a 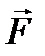- заданная векторная функция того же вида, что и :

.

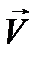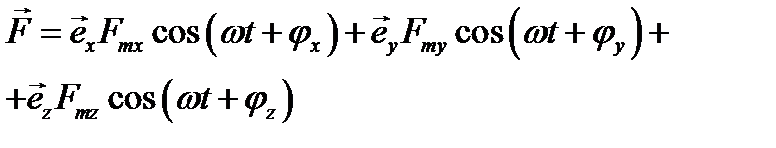В частности, может быть 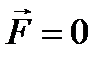, и тогда неоднородное уравнение (12.8) переходит в соответствующее однородное. Заметим также, что векторное уравнение взято в качестве более общего случая, и все дальнейшие рассуждения, разумеется, применимы и к скалярным уравнениям.

Рассмотрим новое уравнение:

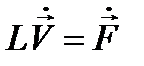. (12.9)

В силу линейности оно распадается на два уравнения относительно вещественных и мнимых частей входящих функций:

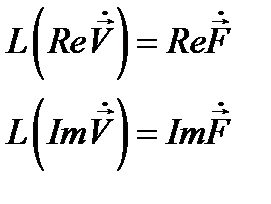(12.9а)

причём первое из этих уравнений не отличается от (12.8), поскольку 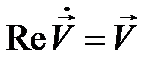и 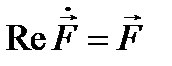. Это значит, что вещественная часть решения уравнения (12.9) удовлетворяет первоначальному уравнению (12.8).

Мы видим, что вместо (12.8) молено решать уравнение (12.9), и затем разыскиваемую функцию 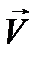получать как вещественную часть найденного решения 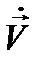.Преимущество такого подхода - в исключении временной зависимости.Действительно, операции дифференцирования и интегрирования, по времени под знаком оператора L в (12.9) сводятся к умножению и, соответственно, делению функции 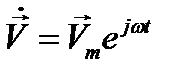на jω, так что

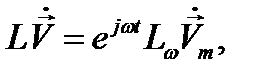
где L_ω - зависящий от ω оператор, который выражает лишь дифференцирование или (и) интегрирование по координатам х, y, z. Внося это в (12.9) и исключая слева и справа общий множитель 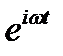, имеем:

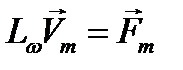(12.10)

Таким образом, вместо первоначального уравнения (12.8) относительно функции координат и времени 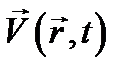получено уравнение (12.10) относительно комплексной амплитуды 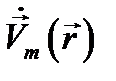функции координат.

Метод комплексных амплитуд состоит в том, что заданное уравнение типа (12.8) приводится к виду (12.10),а после того как оно решено, и функция координат 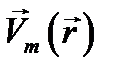найдена, разыскиваемая функция координат и времени 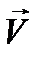получается согласно (12.6) как вещественная часть от .

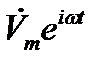В качестве примера обратимся к уравнениям (7.11) и (7.12). Оператор L в этом случае имеет вид:

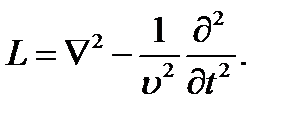
Заменяя дифференцирование по t умножением на jω, получаем здесь следующий оператор L_ω:

.

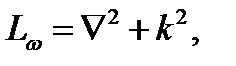
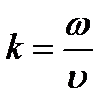Поэтому, в частности, волновое уравнение (7.11) относительно функции 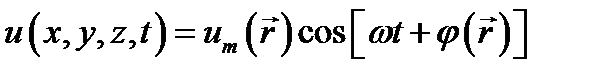переходит в уравнение

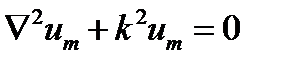(12.11)

относительно комплексной амплитуды 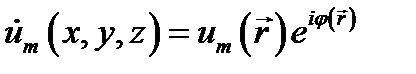. Это так называемое уравнение Гельмгольца.

12.3. Средние значения.Говорят, что величина 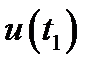есть «мгновенное значение» функции u(t) (12.1) для момента t₁. Если есть какая-либо функция от u(t), которую обозначим F = F[u(t)], то можно говорить и о её мгновенном значении для момента t₁ равном F[u(t₁)]. Но часто представляет интерес также среднее значениеF, под которым понимают

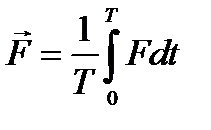(12.12)

Очевидно, в частности, что для F=u

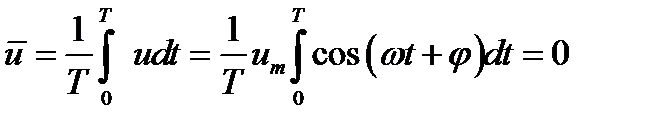, (12.13)

a

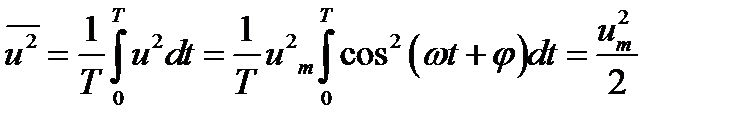. (12.14)

Можно также написать:

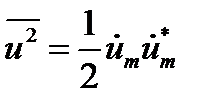, (12.14а)

где звездочка означает комплексное сопряжение (если 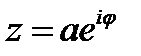,то 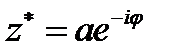).Поэтому для векторной функции 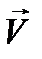вида (12.4) получаем:

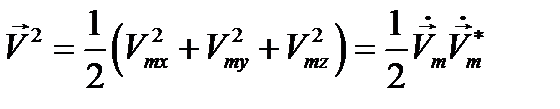, (12.15)

где 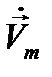есть комплексная амплитуда (12.7). Очевидно 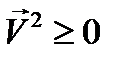, а также

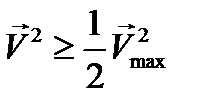(12..16)

В случае произведения функций

и = и_т cos (ω t + φ) и υ = υ_m cos (ωt +φ)

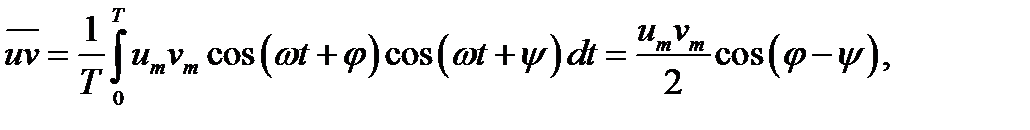(12.17)

или

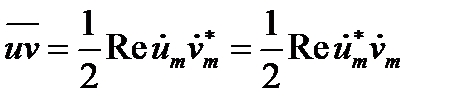(12.17a)

Взяв две векторные функци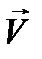и и 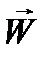вида (12.4), получим соответственно:

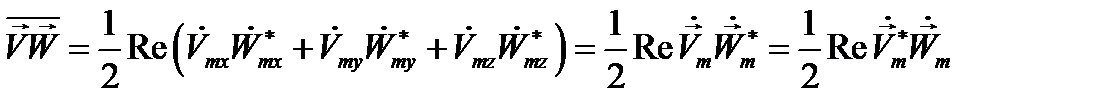(12.18)

Совершенно так же для векторного произведения 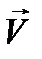и :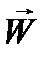

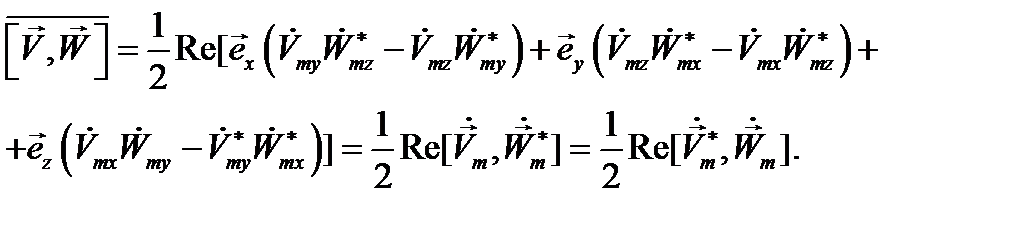(12.19)

Употребление комплексных амплитуд в выражениях средних квадратов и произведений колеблющихся величин не имеет прямой связи с методом комплексных амплитуд, изложенным в п. 2. Очевидно, что

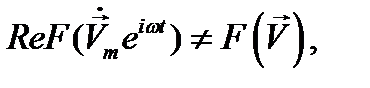
если зависимость 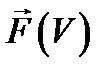не является линейной, в частности, если 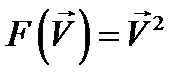. Поэтому мгновенное значение 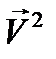нельзя определить как вещественную часть от 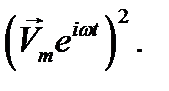Может, однако, оказаться, что комплексные амплитуды желательно ввести в то или иное выражение нелинейной зависимости. Тогда делают подстановку, используя очевидное равенство:

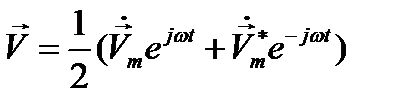(12.20)

Так, например,

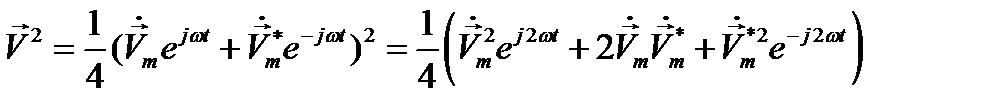(12.21)

12.4. Разложение по гармоническим колебаниям. Наконец, пусть в уравнении (12.8) зависимость 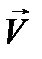и 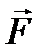от времени сложнее гармонических колебаний. Если она является все же периодической (период Т), то можно воспользоваться представлением функци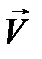и и 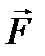в виде рядов Фурье; при этом удобна комплексная форма записи. Так для 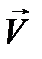имеем:

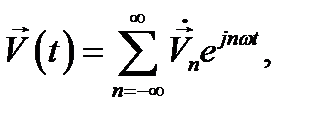(12.22)

где 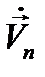- коэффициенты Фурье, связанные с неизвестной 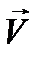соотношением:

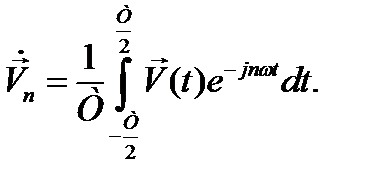(12.23)

Совершенно так же разлагается в ряд Фурье известная функция 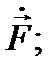её коэффициенты Фурье 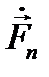можно считать известными. Внося полученные разложения для 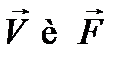в (12.8), получим следующие уравнения для коэффициентов Фурье 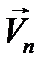, аналогичные уравнению (12.10):

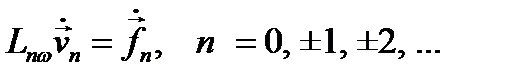. (12.24)

В случае произвольной зависимости от времени функции 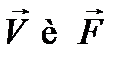можно представить в виде интегралов Фурье:

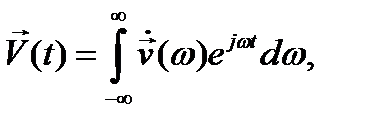(12.25)

где неизвестная спектральная плотность

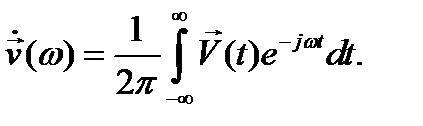(12.26)

При этом из (12.8) для неё получается уравнение:

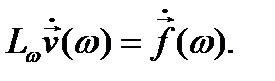(12.27)

Здесь 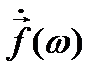- спектральная плотность известной функции .

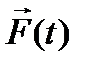Представление 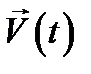в виде ряда Фурье (12.22) или интеграла Фурье (12.25) означает разложение её на гармонические колебания, причём 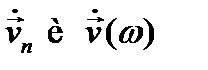имеют смысл комплексных амплитуд, к нахождению которых сводится задача.