Метод Дэвидона-Флетчера-Пауэла

Этот метод имеет и другие названия - метод переменной метрики, квазиньютоновский метод, т.к. он использует оба эти подхода.

Метод Дэвидона-Флетчера-Пауэла (ДФП) основан на использовании ньютоновских направлений, но не требует вычисления обратного гессиана на каждом шаге. Направление поиска на шаге k является направлением 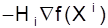, где Hi- положительно определенная симметричная матрица, которая обновляется на каждом шаге и в пределе становится равной обратному гессиану. В качестве начальной матрицы H обычно выбирают единичную. Итерационная процедура ДФП может быть представлена следующим образом:

1. На шаге k имеются точка Xkи положительно определенная матрица Hk.

2. В качестве нового направления поиска выбирается

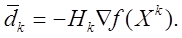
3. Одномерным поиском (обычно кубической интерполяцией) вдоль направления 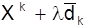определяется lk, минимизирующее функцию .

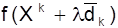4. Полагается .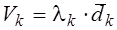

5. Полагается .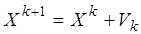

6. Определяется 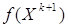и 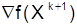. Если |V_k| или 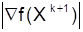достаточно малы, процедура завершается.

7. Полагается U_k = Ñf(X^k+1) - Ñf(X^k).

8. Матрица Hkобновляется по формуле

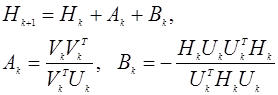
9. Увеличить k на единицу и вернуться на шаг 2.

Метод эффективен на практике, если ошибка вычислений градиента 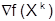невелика и матрица Hkне становится плохо обусловленной.

Матрица Akобеспечивает сходимость Hkк G-1, матрица Bkобеспечивает положительную определенность Hk+1на всех этапах и в пределе исключает H0.

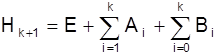
В случае квадратичной функции 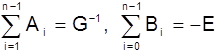, т.е. алгоритм ДФП использует сопряженные направления.

Таким образом, метод ДФП использует как идеи ньютоновского подхода, так и свойства сопряженных направлений, и при минимизации квадратичной функции сходится не более чем за n итераций. Если оптимизируемая функция имеет вид, близкий к квадратичной функции, то метод ДФП эффективен за счет хорошей аппроксимации G-1(метод Ньютона). Если же целевая функция имеет общий вид, то метод ДФП эффективен за счет использования сопряженных направлений.

На практике оказалось, что метод ДФП может давать отрицательные шаги или окончиться в нестационарной точке. Это возможно, когда Hk+1становится плохо обусловленной. Этого можно избежать путем увеличения числа получаемых значимых цифр или перезаданием матрицы Hk+1в виде специальной диагональной матрицы H, где

.

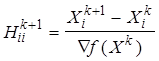Ошибки округления и особенно неточность линейного поиска может послужить причиной потери устойчивости метода ДФП и даже привести к ошибочным шагам, когда значение целевой функции на некоторой итерации возрастает вместо того, чтобы уменьшаться.

По классификации Ньютоновских методов данный алгоритм является квази-Ньютоновским, хотя он использует в явном виде только первые частные производные, а значит, может рассматриваться и как градиентный метод.

Практическая проверка эффективности алгоритма показала, что он столь же эффективен, как и метод Флетчера-Ривса.