Теории Кармана

Гипотеза прямых нормалей (гипотеза Кирхгофа), используемая при выводе дифференциальных уравнений тонких пластин, заключается в следующем:

1) совокупность точек, лежащих па перпендикуляре к срединной поверхности до деформации, остается на перпендикуляре к срединной поверхности и после деформации, при этом отстояние точек от срединной поверхности остается неизменным;

2) нормальными напряжениями, действующими в площадках, параллельных срединной поверхности, можно пренебречь по сравнению с другими напряжениями.

Как видно из вышесказанного, гипотеза прямых нормалей, используемая для построения теории изгиба тонких пластин. аналогична гипотезе плоских сечений, принимаемой при исследовании изгиба балок. Следует отметить, что здесь так же, как и в теории изгиба балок, указанное в п. 1 положение равносильно пренебрежению касательными напряжениями в сечениях, перпендикулярных срединной поверхности и направленных перпендикулярно к этой поверхности. Такое пренебрежение касательными напряжениями, а следовательно, и деформациями сдвига вполне допустимо при определении закона изменения деформаций по толщине пластины, но недопустимо при составлении условий равновесия элемента, выделенного из пластины, так как в условиях равновесия они играют существенную роль. Отмеченное противоречие при применении исходных допущений объясняется тем, что при изгибе Пластины величина углов поворота волокон, которые до деформации были перпендикулярны срединной поверхности, обычно велики по сравнению с указанными деформациями сдвига. Поэтому при определении углов поворота этими деформациями можно пренебречь как мало влияющими на направление волокна после изгиба пластины. Что касается нормальных напряжений, действующих в площадках, параллельных срединной поверхности (п. 2), то их величина для тонких пластин оказывается пренебрежимо малой по сравнению с нормальными напряжениями, действующими в площадках, перпендикулярных срединной поверхности.

Действительно, поперечная нагрузка, действующая на одну сторону судовых пластин, не превосходит нескольких килограммов на сантиметр в квадрате, а на другой стороне равна нулю, в то время как нормальные напряжения в других сечениях достигают 1500—2000 кг/см². Вызванные этими же напряжениями деформации в направлении, перпендикулярном срединной поверхности, также пренебрежимо мало влияют на направление волокна после изгиба пластины.

Все сказанное позволяет рассматривать отмеченные в пп. 1 и 2 допущения как пренебрежение некоторыми деформациями сдвига и удлинения при определении направления волокна деформированной пластины.

При такой постановке вопроса отпадают противоречия в задачах определения закона изменения деформаций по толщине пластины и в условиях равновесия элемента, выделенного из пластины.

Следует также отметить, что указанные выше допущения могут быть использованы и для тел, для которых закон Гука неприменим .

Так как мы будем рассматривать теорию изгиба пластин конечного прогиба, то при нахождении зависимости между перемещениями и деформациями нужно будет учесть нелинейные члены, а также влияние усилий в срединной поверхности на изгиб.

При исследовании изгиба прямоугольных пластин будем пользоваться декартовой системой координат. Плоскость хоу совместим со срединной плоскостью пластины, а ось оz направим вниз.

Размеры пластин в направлении осей ох и оу обозначим буквами а и b соответственно, а толщину пластины—буквой h (рис. 2).

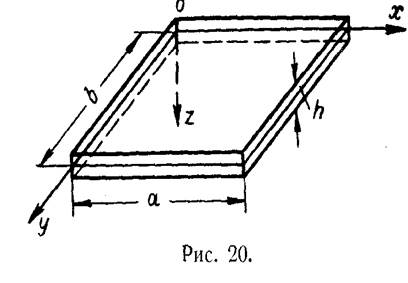
Рис.2

Положительные направления усилий и моментов, соответствующие формулам (133) и (134), показаны на рис. 23,а.

Нетрудно при помощи формул (130) выразить Т₁, Т₂, S, М₁, М₂, Н через перемещения точек срединной поверхности.

Подставляя зависимости (130) в формулы (133) и (134) и учитывая равенства (126) и (135), получим

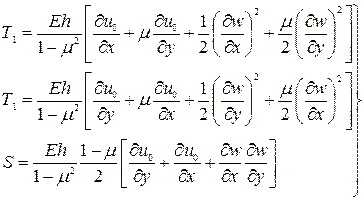(136)

и

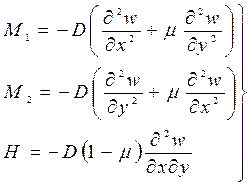(137)

где 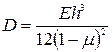- цилиндрическая жесткость пластины.

Формулы (137) дают связь между перемещением w(прогибом пластины) и моментами, действующими в ее поперечном сечении. Усилия же Т₁, Т₂ и S при помощи формул (136) связаны не только с перемещением w, но и с перемещениями u₀, точек срединной поверхности.

Так как перемещения u₀, и v₀ предполагаются непрерывными, то между усилиями Т₁, Т₂ и S можно установить связь, не зависящую от перемещений u₀, и v₀

Умножив вторую формулу (136) на 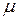и вычтя ее из первой, получим

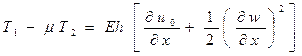(138)

Умножив первую формулу (136) на и вычтя ее из второй, найдем

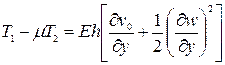(139)

Перепишем третью формулу (136) в виде

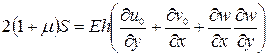(140)

Выражения для интенсивности усилий, приложенных к кромкам пластины, запишутся в виде

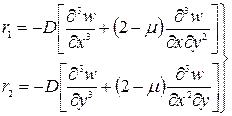(164)

Таким образом, для совершенно свободной кромки у = const три условия (160) можно заменить двумя

М₂=0;

г₂ =0,

используя формулы (137) и (164), нетрудно получить

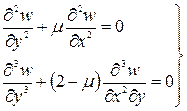(165)

6. Кромка пластины свободно оперта на упругое ребро, жесткость которого ЕI.

Пусть кромка у = const находится в указанных условиях.