Тпелі процестерді операторлық әдіспен есептеу
Азақстан Республикасының Білім және Ғылым Министрлігі
Еуразия Ұлттық Университеті
ТжТ Кафедрасы
КУРСТЫҚ ЖҰМЫС
ЭЛЕКТР ТІЗБЕКТІНДЕГІ
ӨТПЕЛI ҮДЕРІСТЕРДІ ТАЛДАУ
Орындаған: Салимжанов С.
Группа: РЭТ-21
Пәні: ЭТТ-2
Тексерген: Мұхамедрахимов Қ.У.
Астана 2012
Мазмұны
І. Кіріспе.........................................................................................3
Өтпелі үдерістер туралы жалпы мағлұмат
ІІ. Негізгі бөлім.........................................................................4-10
1) Өтпелі процестерді классикалық әдіспен есептеу.............4
2) Өтпелі процестерді операторлық әдіспен есептеу.............6
3) Есептің қойылымы ...............................................................8
4) Есептің шешімі......................................................................8
ІІІ. Қорытынды………………………………………………….11
ІV. Пайдаланған әдебиеттер тізімі............................................12
Кіріспе
E - ЭҚК көзіне қосылған R, L және C элементтерінен құрылған тізбектердегі өтпелi үдерістерді қарастырамыз. Өтпелi деп аталуының себебі – бір-бірінен айырмашылығы бар орнатылған екі тәртіп арасындағы тізбектегі үдеріс болып табылады: t = 0 уақыт моментінде кілтті қосу және ажырату:
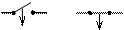 Þ
Þ
Өтпелi үдерістің пайда болуы коммутациямен шартталған.
Орналасу орнына байланысты кілт ток көзін немесе оның бөлек элементтерін тізбекке қосады (тізбектен ажыратады). Осы моменттен бастап талданатын өтпелi үдеріс басталады.
Біз тек уақытқа тәуелді мынадай функцияларды қарастырамыз: тізбек элементтеріндегі i(t) токтарды және сол элементтеріндегі u(t) кернеулерді.
Бұл шамалардың уақытқа тәуелді өзгеруі күрделі өзгеруі мүмкін, сондықтан оларды алдын-ала болжау қиын. Бұл жағдайларды мынадай коммутация заңдарымен өрнектеуге болады.
Индуктивтіліктегі ток және сиымдылықтағы кернеу коммутациядан кейін (t = 0+ уақыт моментіндегі) бірден бұрынғы, коммутацияға дейінгі қалпында (t = 0– уақыт моментіндегі) қалады.
Қысқаша жазылуы: iL (0- ) = iL (0+) және uC (0- ) = uC (0+).
2.1. Өтпелі процестерді классикалық әдіспен есептеу (бастапқы шарттары нольдік екінші дәрежелі тізбек )
t ³ 0 үшін iL(t) және uC(t) есептейміз:
Коммутация моментіндегі және одан кейінгі индуктивті 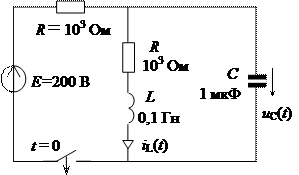 және сиымдылық элементтеріндегі кернеу мен тармақтардарғы токтар есептелінеді.
және сиымдылық элементтеріндегі кернеу мен тармақтардарғы токтар есептелінеді.
Коммутацияға дейін айырылып тұрған ток көзі бар тізбектегі кілт бастапқы нольдік шарттарды: iL(0-) = 0 и uC(0-) = 0 алдын ала анықтайды.
Осы шамалардың әрқайсысы үшін шешімдерді еріксіз және еркiн құраушыларының суммасы түрінде құрамыз:
iL(t) = iLерсіз + iLеркін;
uC(t) = uLCерсіз + uCеркін.
Е - ЭҚК көзімен еріксіз болуға мәжбүр етілген бір құраушысы оның формасын қайталайды және өтпелі үдеріс кезінде өзгеріске ұшырамайды. Бұл жағдай өтпелі үдеріс аяқталғанда құраушыны анықтауға мүмкіндік береді. Осы кезде t = ¥ уақыт моменті үшін құрастырылған тізбекті қолданған ыңғайлы. Тәртіп – орнатылған болғандықтан, uC(¥) = сonst, iC(¥) = 0, iL(¥) = сonst, uL(¥) = 0 деп жазуға болады.
Бұл тәуелділіктер сиымдылықты тізбектегі тармақтың үзiлумен сипаттауға болады, ал индуктивтілікті – қысқа жалғаумен сипаттауға болады.
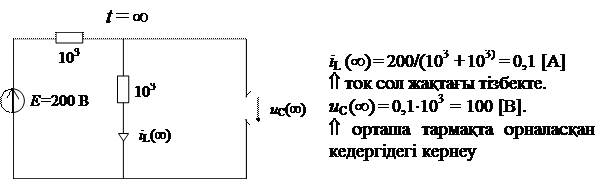
Басқа құраушыға ток көзінің әсері жоқ және индуктивтілік пен сиымдылықтағы электрлік және магниттік өрістердегі энергиялар өзгерісі есебінен пайда болады:
iLсв = A×e×l t + B×el t, uCсв = C×el t + D×el t.
A, B, C және D – интеграл тұрақтылары; l – характеристикалық теңдеудің түбірлері. Бұл теңдеу Z(l) кедергісінде алдын-ала болжанып бағдарламалалғанып, мына тізбектің үш қысқыштарының кез-келгенінде жазылып қойған. Мысалы, ортадағы тармақ үшін ол нольге теңестірілген және характеристикалық болып табылатын кедергі.
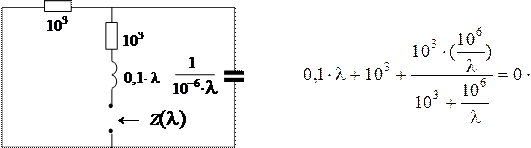 |
Бірқатар өзгертулерден кейін мынадай өрнекті аламыз l2 + 11×103 ×l + 2×107 = 0. Бұл теңдеудің түбірлері: l1 = - 2300 и l2 = - 8700.
Мәжбүр және еркін құраушыларды біріктіріп, төмендегі шешімдерді аламыз
iL(t) = iLпр + iLсв = iL(¥) + A×e-2300×t + B×e-8700×t,
uC(t) = uLCпр + uCсв = uC(¥) + C×e-2300×t + D×e-8700×t.
Соңғы екі теңдеу мынадай түрге келеді
iL(t) = 0,1 + A×e-2300×t + B×e-8700×t, uC(t) = 100 + C×e-2300×t + D×e-8700×t.
A, B, C және D интеграл тұрақтыларын анықтау үшін теңдеулердің екі жүйесін құрамыз. Ол үшін iL(t), uC(t) және коммутацидан кейінгі олардың туындыларын қаратсырамыз. Ток пен кернеудің туындыларының
 |
физикалық мәні бар:L× diL /dt = uL(t), C× duC /dt = iC(t).
t(0+) моментіндегі орнын басушы тізбекі мынадай болады:
Ток iL(t) = 0,1 + A×e-2300×t + B×e-8700×t в момент t = 0+ моментінде iL(t) = 0,1 + A×e-2300×t + B×e-8700×t тогы, iL(0+) = 0 ескергенде, мынадай:
iL(0+) = 0,1 + A + B; iL(0+) = A + B = - 0,1
uL(0+) = 0 ескергенде, t = 0+ моментінде кернеу uL(t) = L×diL /dt = 0,1[-2300×A×e-2300×t-8700×B×e-8700×t] мынадай болады:
uL(0+) = 0,1[ -2300×A -8700×B] немесе 2,3×A + 8,7×B = 0.
uC(0+) = 0 ескергенде, t = 0+ моментінде кернеу uC(t) = 100 + C×e-2300×t + D×e-8700×t мынадай болады:
uC(0+) = 100 + C + D или C + D = - 100 .
iC(0+) = 0,2A ескергенде, t = 0+ моментінде ток iC(t) = C× duC /dt = 10-6[-2300×C×e-2300×t-8700×D×e-8700×t] мынадай болады:
0,2 = 10-6[- 2300×C - 8700×D] немесе 2,3×C + 8,7×D = -200.
Теңдеулердің екі жүйесін аламыз:
A + B = - 0,1; C + D = - 100;
2,3×A + 8,7×B = 0. 2,3×C + 8,7×D = - 200.
Бұл жүйелерді шешу барысында интегралдау тұрақтыларын табамыз:
А = - 0,1359 және В = - 0,0359; C = -104,7 және D = - 4,7.
A, B, C және D мәнрдерін жоғарыдағы шешімдерге қойғанда, интуктивтіліктегі токтың және сыйымдылықтағы кернеудің мәндерін уақытқа тәуелді функция түрінде анықтаймыз
iL(t) = 0,1 - 0,1359×e-2300t + 0,0359e-8700t, [A];
uC(t) = 100 - 104,7×e-2300t + 4,7e-8700t, [B].
Жоғарыда алынған қатынастар басқа да токтар мен кернеулердің мәндерін анықзтауға мүмкіндік береді:
iC(t) = C duC/dt = 10-6×[104,7×2300×e-2300t - 4,7×8700×e-8700t] =
=0,2406×e-2300t -0,0406×e-8700t [A];
uL(t) = L diL/dt = 0,1×[0,1359×2300×e-2300t - 0,0359×8700×e-8700t] =
= 31,26×e-2300t -31,26×e-8700t [B];
i(t) = iL + iC = 0,1 + 0,1047×e-2300t - 0,0047×e-8700t[A].
тпелі процестерді операторлық әдіспен есептеу
 | |||
 |
Бөлімнің полиномының түбірлерін есептеп: p1 = 0; p2,3 = - 59,5± j 210, мультипликативтік түрдегі полиномды жазамыз.
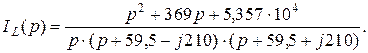 |
Кері түрлендіруді шегермелердiң теоремасы бойынша орындаймыз.
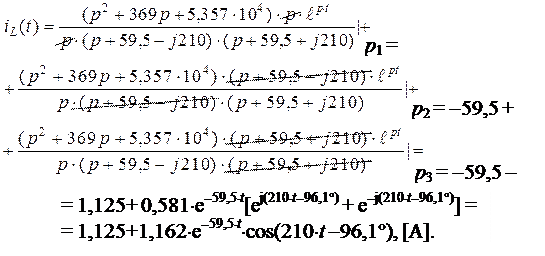 |
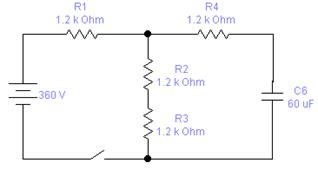
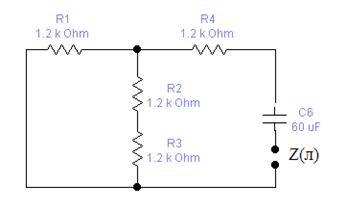
ТАПСЫРМА 1. Бірінші текті тізбектегі өтпелі үдерісті талдауды орындау қажет. Тізбектің схемасы 1 суретте қорытылған түрде бейнеленген. Бастапқы шарттар нольдік.
 |
1-сурет
Зерттеу алдында, кестедегі информацияны қолданып, тізбектің схемасын құрастыру қажет.
| Нұсқа | E [B] | R [кОм] | L [мГн] | C [мкФ] | Анықталатын шамалар |
| R1=R2=R3=R4=1,2 | - | C6=60 | i3(t); u2(t) |
Есептің шешімі: (Классикалық әдіс)
UC(0-) = UC(0+) =0 ; UC(t) = UCерсіз + UCеркін.
UC(t) = ULC ерсіз + UCеркін = UC(¥) + A×elt
UC(¥) = (R2+R3)I2=2R I2
I2 = E/ (R1+R2+R3)= E/3R
UC(¥) = (R2+R3)I2=2R E/3R = 2E/3
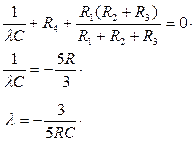
UC(t) = UC(¥) + A×elt , t=0
0 = 2E/3 + A, A = -2E/3
UC(t) = 2E/3 -2E/3 ×e 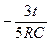 = 2E/3(1-e
= 2E/3(1-e 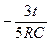 )
)
iC(t) = C× duC /dt = C ×2E/R ( 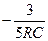 ×e
×e 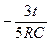 ) =
) = 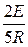 ×e
×e 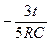
i3(t) = 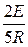 ×e
×e 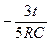
U2 + U3 = UC +U4
2U = RI3 + UC
U = 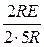 ×e
×e 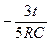 +
+ 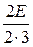 -
- 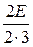 ×e
×e 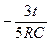 =
= 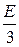 -
- 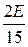 ×e
×e 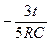
u2(t) = 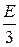 -
- 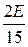 ×e
×e 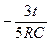
Операторлық әдіспен талдау:
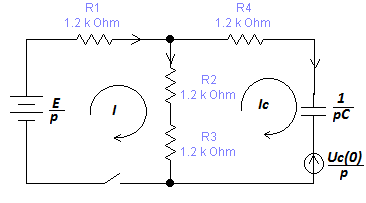
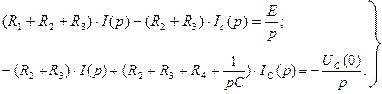 Талдау үшін контурлық токтар әдісін қолданамыз:
Талдау үшін контурлық токтар әдісін қолданамыз:
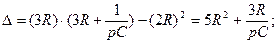 | |||
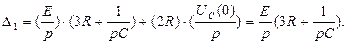 | |||
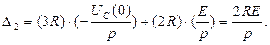 |
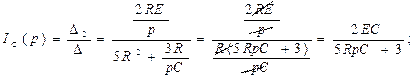
F1=2EC
F2=1
F3=5RpC+3
5RpC+3=0
p= 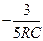
IC(t) = 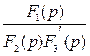 ×ept=
×ept= 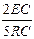 ×ept=
×ept= 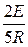 ×e
×e 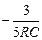 t
t
i3(t) = 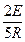 ×e
×e 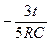
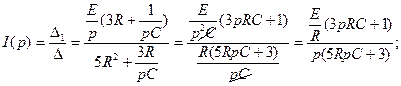 |
F1= 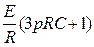
F2=p
F3=5RpC+3
5RpC+3=0
p1 = 0, p2= 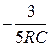
 I (t) =
I (t) = 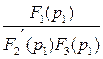 ×ept +
×ept + 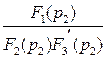 ×ept =
×ept = 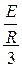 +
+ 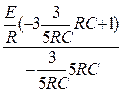 ×e
×e 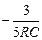 t= =
t= = 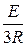 +
+ 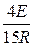 ×e
×e 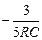 t
t
I2(t) = i (t) –iC(t) = 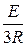 +
+ 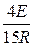 ×e
×e 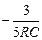 t -
t - 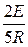 ×e
×e 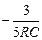 t =
t = 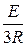 -
- 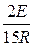 ×e
×e 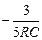 t
t
u2(t) = I2(t)R = ( 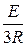 -
- 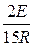 ×e
×e 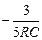 t)R =
t)R = 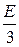 -
- 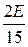 ×e
×e 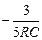 t
t
u2(t) = 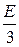 -
- 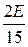 ×e
×e 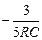 t
t
i3(t) = 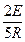 ×e
×e 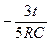
| t (c) | |||||
| i3(t) (A) | 0.1 | 25.5*10-6 | 6.44*10-9 | 1.64*10-12 | 4.23*10-16 |