Сложные зубчатые механизмы с подвижными осями
Если в соосном механизме (рис. 53) блок зубчатых колес z2–z3 закрепить так, чтобы он имел возможность вращаться вокруг оси колес z1–z4, то получим механизм (рис. 54, а), у которого ось колес z2–z3 будет подвижна в пространстве.
а) 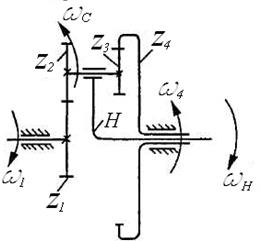 б)
б) 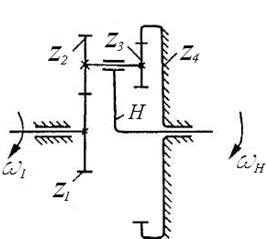
Рис. 54. Механизмы с подвижной осью:
а) W = 2; б) W = 1
Этот так называемый дифференциальный механизм качественно отличается от механизма с неподвижными осями. Он позволяет суммировать или раздваивать движения, так как имеет две степени свободы:
W = 3n – 2 p5 – p4;
W = 3  4 – 2
4 – 2  4 – 2 = 2.
4 – 2 = 2.
Если закрепить неподвижно колесо z4(рис. 54, б), получим механизм
с подвижными осями, имеющий степень свободы W = l – простой планетарный механизм:
W = 3n – 2 p5 – p4;
W = 3  3 – 2
3 – 2  3 – 2 = 1.
3 – 2 = 1.
Подвижный блок в таких механизмах называют сателлитом, держатель сателлитов Н – водилом, а соосные колеса z1и z4 – центральными. Если одно из центральных колес неподвижно (z4 на рис. 54, б), то его называют солнечным.
Для планетарных механизмов передаточное отношение не является отношением чисел зубьев, как это было для механизмов с неподвижными осями. Связь между угловыми скоростями и числами зубьев колес звеньев таких механизмов можно установить методом обращения движения.
Пример. Пусть для рассматриваемого механизма (рис. 54) известны 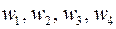 и
и 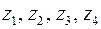 . Сообщим всей системе угловую скорость, обратную и численно равную угловой скорости водила (–
. Сообщим всей системе угловую скорость, обратную и численно равную угловой скорости водила (– 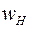 ). Получим эквивалентный в относительном движении исходному механизму новый (обращенный) механизм, у которого водило неподвижно, а угловые скорости звеньев равны:
). Получим эквивалентный в относительном движении исходному механизму новый (обращенный) механизм, у которого водило неподвижно, а угловые скорости звеньев равны:
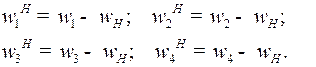
Верхний индекс Н указывает на систему отсчета, т. е. неподвижность звена – в данном случае неподвижно водило.
Такой механизм является соосным механизмом с неподвижными осями в пространстве (рис. 90) с передаточным отношением:
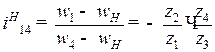 . (7.5)
. (7.5)
В общем виде при числе зубчатых колес n получим:
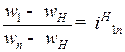 . (7.6)
. (7.6)
Метод обращения движения иначе называют методом Виллиса, а последняя зависимость (8.6) получила название формулы Виллиса.
Механизмы с подвижными осями (планетарные механизмы) подразделяются на следующее:
- дифференциальные (при W > 1);
- простые планетарные (W = 1);
- замкнутые планетарные (получаемые из дифференциальных механизмов наложением замыкающей связи между двумя центральными валами).
Планетарные механизмы имеют следующие возможности:
- позволяют получить очень большие передаточные отношения при малом числе сателлитов;
- позволяют выполнить раздачу движения и мощности от одного двигателя нескольким потребителям при W > 1 (дифференциал заднего моста автомобиля и т. п.);
- позволяют складывать движения (суммирующие механизмы);
- позволяют получать различные сложные траектории точек сателлитов.
Для уменьшения габаритов и веса (вес может быть в 2 – 6 раз меньше, чем у механизма с неподвижными осями), разгрузки центральных валов от изгиба, для уравновешивания центробежных сил сателлитов применяют несколько сателлитов (несколько пар саттелитов), как правило, равномерно расположенных по окружности (в силовых передачах число k таких сателлитов достигает 20). Многосателлитные планетарные механизмы имеют разветвление силовых потоков, что позволяет снизить вес и повышает надежность работы за счет параллельного резервирования.
Планетарные механизмы имеют статическую неопределимость при k > 1
и более высокий уровень конструктивной сложности.
Наибольшеераспространение получили простые планетарные механизмы различных кинематических схем. Самые простые и самые распространенные из них показаны на рис. 55.
а) 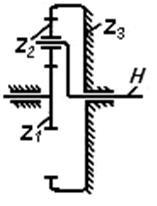 б)
б) 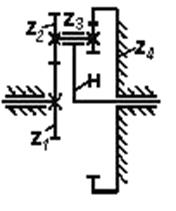
в) 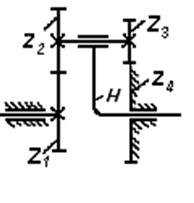 г)
г) 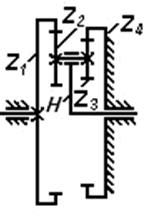
Рис. 55. Простые планетарные механизмы:
а) 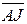 -механизм; б) АJ-механизм; в) AA-механизм; г) JJ-механизм
-механизм; б) АJ-механизм; в) AA-механизм; г) JJ-механизм
Примечание. В условные обозначения планетарных механизмов входят обозначения видов зацеплений – внешнее (А) и внутреннее (J).
Подбор чисел зубьев простых планетарных механизмов
При подборе чисел зубьев должно быть выполнено много условий.
К числу обязательных условий относятся:
- уравнение передаточного отношения;
- уравнение соосности;
- условие соседства (для простых схем при k > 3);
- условие сборки (при k > 2).
В качестве дополнительных условий или условий оптимизации могут быть приняты в зависимости от предъявляемых требований следующие условия:
- обеспечение высокого коэффициента полезного действия проектируемого механизма;
- обеспечение прочности зубчатых зацеплений и равнопрочности всех ступеней;
- достижение минимальной массы и габаритов;
- обеспечение максимальной точности работы механизма;
- обеспечение равного модуля по ступеням;
- обеспечение наибольшей работоспособности подшипников сателлитов
и другие условия.
Даже выполнение части перечисленных условий оптимизации представляет сложную задачу многокритериального синтеза, решаемую с применением современных ПК.
Рассмотрим основные условия для подбора чисел зубьев колес планетарных механизмов.
Уравнение передаточного отношения для планетарных механизмов составляется с обязательным использованием формулы Виллиса (8.6) при 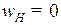 :
:
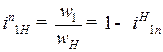 ,(7.18)
,(7.18)
где n = 3; 4.
Например, для AA-механизма: 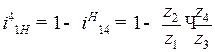 .
.
Передаточное отношение от водила к первому колесу:
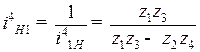 .
.
Выбрав разность ( 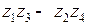 ) достаточно малой, можно получить очень большое передаточное отношение
) достаточно малой, можно получить очень большое передаточное отношение 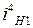 при двух зацеплениях.
при двух зацеплениях.
Уравнение соосности записывается аналогично уравнениям (7.2), (7.3), (8.4) для соосного механизма (см. рис. 53).
При постановке нескольких сателлитов, равномерно расположенных по окружности, должно выполняться условие размещения их вокруг центрального колеса, или условие соседства.
Например, для AJ-механизма (рис. 56) необходимо, чтобы 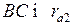 .
.
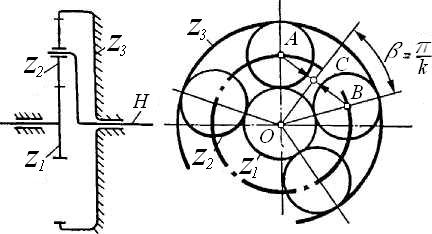
Рис. 56. К определению условия соседства
Здесь:
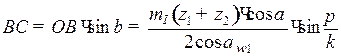 ;
;
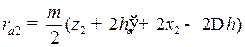 .
.
Для нулевых колес получим:
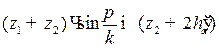 . (7.19)
. (7.19)
Кроме этого, все сателлиты можно одновременно ввести в зацепление с центральными колесами только при определенном соотношении чисел зубьев колес.
Условие зацепляемости, или условие сборки,рассмотрим на примере
AJ-механизма (рис. 57).
Примем для определенности решения, что сателлит z2имеет четное число зубьев. Пусть сателлит I собран с центральными колесами z1 и z3 в положении, когда по линии центров располагаются оси симметрии зубьев центральных колес. Если числа z1 и z3 не кратны числу сателлитов k, то по линии центров ОВ второго сателлита расположатся не оси симметрии зубьев. Ось симметрии ближайшего зуба 1 отстоит от линии центров на дугу 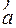 , а зуба 3 – на дугу
, а зуба 3 – на дугу 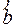 . Очевидно, что центральные дуги между двумя сателлитами можно представить как
. Очевидно, что центральные дуги между двумя сателлитами можно представить как 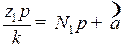 и
и 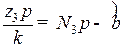 , где N1, N3 – целые числа шагов р на рассматриваемых дугах.
, где N1, N3 – целые числа шагов р на рассматриваемых дугах.
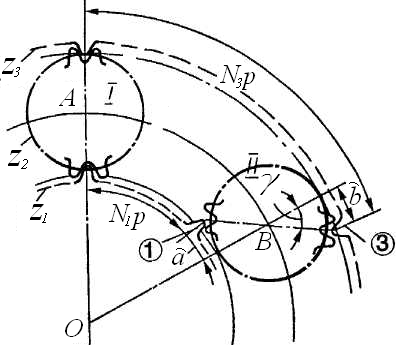
Рис. 57. К определению условия сборки
Если удалось ввести в зацепление сателлит II, то его общая ось впадин отклонится от линии центров на угол 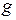 (в этом случае
(в этом случае 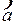 =
= 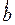 ). Из предыдущих равенств имеем
). Из предыдущих равенств имеем
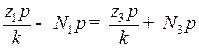 .
.
Отсюда:
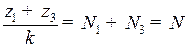 , (7.20)
, (7.20)
где N – любое целое число.
Таким образом, сборка AJ-механизма выполнима, если сумма зубьев центральных колес кратна числу сателлитов.
Для каждого вида планетарных механизмов условие сборки имеет свой вид.
В силу того, что условие соседства представляет собой неравенство, а условие сборки даст новые неизвестные целые числа, перечисленных четырех условий недостаточно для нахождения чисел зубьев. Поэтому задача по определению чисел зубьев решается подбором.
