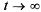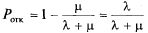Системы массового обслуживания с отказами
Одноканальная СМО с отказами
Простейшей из всех задач теории массового обслуживания является модель одноканальной СМО с отказами (потерями).
При этом система массового обслуживания состоит только из одного канала (n = 1) и на нее поступает пуассоновский поток заявок с интенсивностью 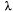 , зависящей, в общем случае, от времени:
, зависящей, в общем случае, от времени:
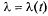
Заявка, заставшая канал занятым, получает отказ и покидает систему. Обслуживание заявки продолжается в течение случайного времени 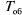 ,
,
Из этого следует, что «поток обслуживания» — простейший, с интенсивностью 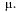 Чтобы представить себе этот поток, вообразим один непрерывно занятый канал, который будет выдавать обслуженные заявки потоком с интенсивностью
Чтобы представить себе этот поток, вообразим один непрерывно занятый канал, который будет выдавать обслуженные заявки потоком с интенсивностью 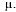
Рассмотрим единственный канал обслуживания как физическую систему S, которая может находиться в одном из двух состояний: 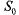 — свободен,
— свободен,  — занят.
— занят.
ГСП системы показан на рис. 5.6, а.
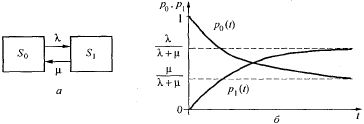
Рис. 5.6. ГСП для одноканальной СМО с отказами (а); график решения уравнения (5.38) (б)
Из состояния  в
в  систему, очевидно, переводит поток заявок с интенсивностью
систему, очевидно, переводит поток заявок с интенсивностью 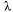 ; из
; из 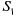 в
в 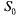 — «поток обслуживания» с интенсивностью
— «поток обслуживания» с интенсивностью 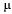 .
.
Вероятности состояний: 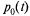 и
и 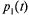 . Очевидно, для любого момента t:
. Очевидно, для любого момента t:
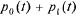 = 1. (5.36)
= 1. (5.36)
Составим дифференциальные уравнения Колмогорова для вероятностей состояний согласно правилу, данному выше:
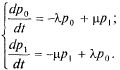 (5.37) эрланг
(5.37) эрланг
Из двух уравнений (5.37) одно является лишним, так как 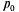 и
и 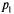 связаны соотношением (5.36). Учитывая это, отбросим второе уравнение, а в первое подставим вместо
связаны соотношением (5.36). Учитывая это, отбросим второе уравнение, а в первое подставим вместо 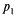 выражение
выражение 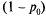 :
:
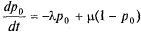
или
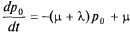 (5.38)
(5.38)
Поскольку в начальный момент канал свободен, уравнение следует решать при начальных условиях: 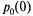 = 1,
= 1, 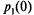 =0.
=0.
Линейное дифференциальное уравнение (5.38) с одной неизвестной функцией 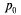 легко может быть решено не только для простейшего потока заявок
легко может быть решено не только для простейшего потока заявок 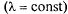 , но и для случая, когда интенсивность этого потока со временем меняется.
, но и для случая, когда интенсивность этого потока со временем меняется.
Для первого случая решение есть:
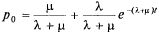
Зависимость величины 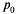 от времени имеет вид, изображенный на рис. 5.6, б. В начальный момент (при t = 0) канал заведомо свободен (
от времени имеет вид, изображенный на рис. 5.6, б. В начальный момент (при t = 0) канал заведомо свободен ( 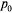 (0) = 1). С увеличением t вероятность
(0) = 1). С увеличением t вероятность 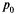 уменьшается и в пределе (при
уменьшается и в пределе (при 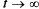 ) равна
) равна 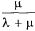 . Величина,
. Величина, 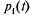 дополняющая
дополняющая 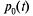 до единицы, изменяется так, как показано на том же рисунке.
до единицы, изменяется так, как показано на том же рисунке.
10. Нетрудно убедиться, что для одноканальной СМО с отказами вероятность 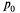 есть не что иное, как относительная пропускная способность q. Действительно,
есть не что иное, как относительная пропускная способность q. Действительно, 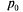 есть вероятность того, что в момент t канал свободен, или вероятность того, что заявка, пришедшая в момент t, будет обслужена. Следовательно, для данного момента времени t среднее отношение числа обслуженных заявок к числу поступивших также равно
есть вероятность того, что в момент t канал свободен, или вероятность того, что заявка, пришедшая в момент t, будет обслужена. Следовательно, для данного момента времени t среднее отношение числа обслуженных заявок к числу поступивших также равно 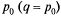
В пределе, при 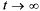 , когда процесс обслуживания уже установится, предельное значение относительной пропускной способности будет равно:
, когда процесс обслуживания уже установится, предельное значение относительной пропускной способности будет равно:
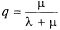
Зная относительную пропускную способность q, легко найти абсолютную А. Они связаны очевидным соотношением:
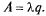
В пределе, при 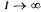 , абсолютная пропускная способность тоже установится и будет равна
, абсолютная пропускная способность тоже установится и будет равна
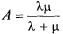
Зная относительную пропускную способность системы q (вероятность того, что пришедшая в момент t заявка будет обслужена), легко найти вероятность отказа:

или среднюю часть необслуженных заявок среди поданных. При