Математиканы оқытудағы салыстыру және анология
Лекция
Жоспары:
1. Салыстыру
2. Аналогия
3. Модельдеу.
1. Салыстыру.Таным әдістерінің ішінде ең көп тараған және әмбебап әдістердің бірі – салыстыру.
Зерттелінетін объективтердің ұқсастықтары мен айырмашылықтарын ойша тағайындау салыстыру деп аталынады. Ғылымда салыстыра отырып байқау және өзгерісті айыра алу, адамның ойлау қызметінің негізін қалайтындығы тағайындалған. Салыстыруға жүгінбей бір де бір қарапайым ұғымның өзін құруға болмайды.
Салыстыру нәтижесінде дұрыс қорытынды алу үшін мынадай шарттар орындалу қажет.
1. Тек біртекті объектілерді салыстыруға болады.
2. Объектілерді бірдей белгісі бойынша салыстыру, ол толық болып аяғына дейін жеткізілу тиіс.
К.Д.Ушинский “дидактикада салыстыру негізгі тәсіл болуы керек”, – деп есептеген. Салыстыра білуді мақсатты қалыптастыру үшін салыстырылатын объектінің нақтылы құрамын, құрылысын оқушылар айқын біліп алуы қажет. Салыстыра білудің мүмкін болатын бір нұсқасы мынадай.
Салыстыру деген, бұл:
а) оқылатын объектілердің елеулі белгілерін бөліп көрсету;
ә) объектіні басқадан бөліктеп тұратын белгілерді табу;
б) осы белгілер арқылы объектілерді салыстыру.
Математикадан сабақ беру кезінде салыстыруды жүйелі және жоспарлы қолдану, білімді тереңдетіп және тиянақтап қана қоймай оқушылардың математикалық ойлауын, жасампаздық және танымдық қабілетін дамытады, ойлау қызметін белсендіреді.
Салыстырудың тану үрдісіндегі маңызы үлкен болғанымен де, ол зерттеліп отырған объект туралы толық білім береді деп айта алмаймыз.
Салыстыруды тану үрдісінің басқа әдістерімен бірегей қолданғанда, бізді қоршаған дүниенің заттары мен құбылыстарын зерттеудің тиімді құралы бола алады.
Математиканы оқыту үрдісінде салыстыруды пайдалануға мысалдар келтірейік.
y
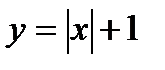
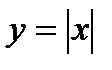
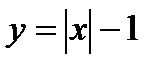
0 x
1-cурет
Функциялардың сызбасын оқып үйренуде салыстыру өте пайдалы. 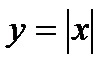 функциясын қарастырайық. Абсолют шаманың анықтамасын пайдалана отырып
функциясын қарастырайық. Абсолют шаманың анықтамасын пайдалана отырып 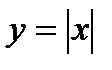 функциясының сызбасын салатын болсақ, оның ордината өсіне симметриялы екенін көреміз (1-сурет).
функциясының сызбасын салатын болсақ, оның ордината өсіне симметриялы екенін көреміз (1-сурет).
Енді 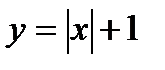 функциясының сызбасын салайық.
функциясының сызбасын салайық. 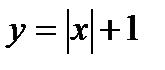 функциясының сызбасы мәндерінің кестесін құрып, оны
функциясының сызбасы мәндерінің кестесін құрып, оны 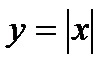 функциясының мәндерімен салыстырсақ, онда бірінші функцияның сызбасы екінші функцияның сызбасын бір бірлікке көтеру нәтижесінде шығады.
функциясының мәндерімен салыстырсақ, онда бірінші функцияның сызбасы екінші функцияның сызбасын бір бірлікке көтеру нәтижесінде шығады.
Ал 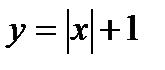 функциясының сызбасын салу үшін
функциясының сызбасын салу үшін 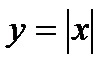 функциясының сызбасын ордината өсі бойымен бір бірлікке төмен жылжыту керек.
функциясының сызбасын ордината өсі бойымен бір бірлікке төмен жылжыту керек.
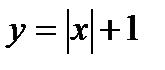 функциясының сызбасын салу ережесін қорыту үшін
функциясының сызбасын салу ережесін қорыту үшін 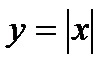 және
және 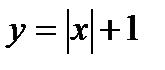 функцияларының мәндерінің кестесін салыстырсақ, екінші функцияның мәндері бірінші функцияның мәндерімен бірдей болғанымен, бір бірлік артық қабылдап отыратындығы байқалады.
функцияларының мәндерінің кестесін салыстырсақ, екінші функцияның мәндері бірінші функцияның мәндерімен бірдей болғанымен, бір бірлік артық қабылдап отыратындығы байқалады.
у
х
-1 0 1
2-сурет
Демек, 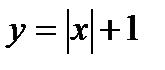 функциясының сызбасы
функциясының сызбасы 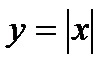 функциясының сызбасын бір бірлікке абсцисса өсі бойымен солға жылжыту нәтижесінде келіп шығады (2-сурет).
функциясының сызбасын бір бірлікке абсцисса өсі бойымен солға жылжыту нәтижесінде келіп шығады (2-сурет).
Ал 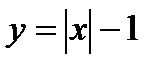 функциясының сызбасы,
функциясының сызбасы, 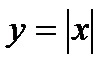 функциясының сызбасын абсцисса өсі бойымен бір бірлікке оңға жылжыту арқылы алынады. Осы функциялардың сызбасын салыстыру арқылы
функциясының сызбасын абсцисса өсі бойымен бір бірлікке оңға жылжыту арқылы алынады. Осы функциялардың сызбасын салыстыру арқылы 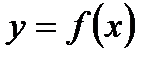 функциясының сызбасы бойынша
функциясының сызбасы бойынша 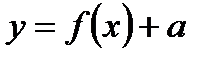 ,
, 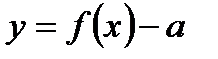 ,
, 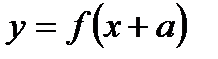 функцияларының сызбасын салу ережелерін тұжырымдауға болады.
функцияларының сызбасын салу ережелерін тұжырымдауға болады.
3. Аналогия және модельдеу. Математикалық объектілердің кейбір
қасиеттерін оқып үйрену барысында, ол қасиеттердің басқа бір бұрыннан белгілі объектілердің қасиеттерімен сәйкес келіп қалуы мүмкін. Осындай сәйкестіктерді тағайындау нәтижесінде, ол объектілердің басқа қасиеттері де сәйкес келеді деп жорамалдауға болады. Осы түрдегі пайымдау аналогияның негізін қалайды.
Аналогияға ең жақын әдіс модельдеу, сондықтан ғылыми пайымдаудағы интеграциялау тенденциясының күшеюіне байланысты модельдеудің маңызы едәуір артып келеді.
3. Аналогия.Аналогия (грекше analogia – сәйкестік, ұқсастық) объектілердің кейбір белгілерінің ұқсастығына сүйеніп, олардың басқа белгілерінің де ұқсас болатындығы туралы қорытынды шығаратын таным әдісі. Аналогия бойынша қорытынды жасауды схемалық түрде былай көрсетуге болады: Егер қарастырылып отырған А және В объектілерінің ортақ қасиеттері 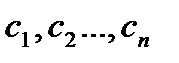 болып және А объекті тағы да d деген қасиетке ие болса, онда В-да d қасиетке ие болады деген қорытынды жасалынады.
болып және А объекті тағы да d деген қасиетке ие болса, онда В-да d қасиетке ие болады деген қорытынды жасалынады.
Аналогия бойынша қорытынды ықтимал ғана болады. Ол ғылыми болжам жасаудың қайнар көзі бола отырып, ғылыми ізденіс жасауда үлкен маңызға ие.
Аналогияның айрықша сипаты – бір жүйедегі қатыстар мен қасиеттерді екінші жүйеге көшіру болып табылады. Оқушылардың бір объектіні оқып үйренудегі білімдерді екінші объектіге көшіру қабілетін қалыптастыру, оқытудағы ең маңызды мәселе.
Сондықтан математика мұғалімі аналогия (үрдісін) әдісін меңгеріп оның әрбір түрін сабақ беру үрдісінде еркін қолдана білуі және аналогия бойынша жасалынып жатқан қорытындыны шындыққа жақындатқан факторларды білуі тиіс.
А.И. Уемовтың зерттеулеріне сүйенетін болсақ, аналогия бойынша жасалған қорытындының ықтималдылығы жоғары болу үшін мынадай шарттар орындалуы тиіс:
1) А және В объектілеріне ортақ белгілер 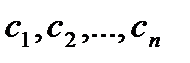 мүмкіндігінше көп болуы қажет;
мүмкіндігінше көп болуы қажет;
2) ол белгілер екі объект үшін де елеулі белгілер болуы тиіс;
3) ол белгілер салыстырып отырған объектілердің әр түрлі жақтарын қамтитын болғаны жөн;
4) екінші объектіге жатқызылатын d белгісі 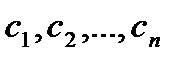 белгілер типтес болуы керек;
белгілер типтес болуы керек;
5) 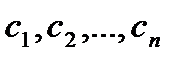 белгілер салыстырылатын объектілердің өзіне ғана тән болып, кез келген объектіге жататын болмауы тиіс;
белгілер салыстырылатын объектілердің өзіне ғана тән болып, кез келген объектіге жататын болмауы тиіс;
6) егер қорытынды аз ақпарат беретін болса, онда шындыққа көбірек жақын болады. Бұл екінші объектіге көшірілетін d белгісі ерекше сипатқа ие болмауы керек дегенді білдіреді.
Енді математикада аналогияны қолдануға мысалдар келтірейік.
Мысалы, көп өлшемді геометрияның негізгі ұғымдарын енгізу жазықтықтағы және үш өлшемді кеңістіктегі негізгі ұғымдардан аналогияны пайдалану нәтижесінде келіп шыққан. Комплекс айнымалысы бар функция нақты айнымалысы бар функцияға аналогия негізінде пайда болған. Комплекс айнымалылар функциясының теориясын құруда нақты айнымалы функцияларды зерттеу әдістерімен аналогияны пайдаланған.
Бұрын оқытылғын материал мен жаңа материалды оқыту арасындағы байланысты тағайындауда аналогияны пайдалануға мысалдар қарастырайық. Мысалы, шардың (сфераның) диаметрі ұғымын енгізуді былайша жүргізуге болады: мектептің планиметрия курсында дөңгелектің (шеңбердің) диаметрі, дөңгелек шеңберінің (шеңбердің) кез келген екі нүктесін қосатын хордалардың (кесінділердің) ең үлкені ретінде анықталады, стереометрияда да шардың (сфераның) диаметрі дәл сол сияқты анықталады.
Мектеп математика курсында екі түзудің параллельдігінің анықтамасынан аналогияны пайдаланып, жазықтықтардың параллельдігі немесе түзу мен жазықтықтың параллельдігінің анықтамалары тұжырымдалады.
Аналогияны мынадай мысал келтірейік. Кез келген тетраэдр үшін
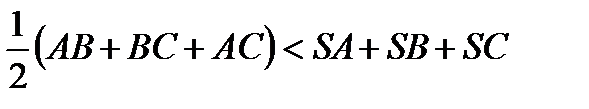
теңсіздігінің орындалатынын дәлелдейік.
Бізге кеңістіктегі тетраэдр фигурасы жазықтықтағы үшбұрыш фигурасына аналогия екені белгілі, сондықтан кез келген үшбұрыш үшін орындалатын төмендегі қасиетті пайдаланамыз.
Бізге кез келген үшбұрыштың екі қабырғасының ұзындығының қосындысы оның үшінші қабырғасының ұзындығынан артық болатыны белгілі (3-сурет). AB+BC>AC.
Егер үшбұрыш үшін орындалатын осы қасиетті оған аналогия болатын –тетраэдр үшін қолдансақ, төмендегі теңсіздіктер келіп шығады (4-сурет):
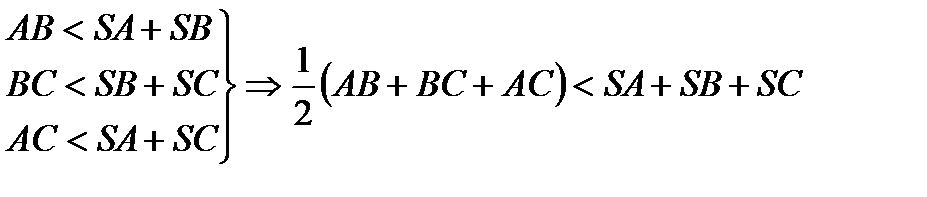
S
В
А С А С
3-сурет В
4-сурет
Аналогия жаңа білімдерді игеруде және оларды практикалық қолдануларда да пайдаланылады. Мысалы, бір есепті шығару жолын іздестіру үшін берілген есепке ұқсас есептер қарастырылады. Бұл ұқсас есеп оңай немесе шығару жолы бұрыннан белгілі болуы тиіс.
Математиканы оқыту кезінде оқушылар аналогияны дұрыс пайдаланбау нәтижесінде көптеген қателер жібереді. Мысалы, шеңберге іштей сызылған тікбұрыш диаметрге тірелетінен аналогияны пайдаланып сфераға іштей сызылған тікбұрышты үш жақты бұрыш әр уақытта сфераның үлкен дөңгелегіне тіреледі деп қорытынды шығарады. Кез келген үшбұрыштың биіктіктері бір нүктеде қиылысады, бірақ ол кез келген тетраэдр үшін дұрыс бола бермейді. Бұл қателіктердің негізгі себебі оқушылар бір объектінің қасиеттерін екінші бір объектіге аудару кезінде ол касиеттердің бір-бірінен айырмашылығына көңіл аудармайды. Мәселен, 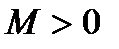 ,
,  болғандағы
болғандағы 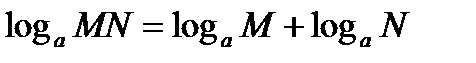 формуласынан аналогияны пайдаланып мынадай қате формула жазады:
формуласынан аналогияны пайдаланып мынадай қате формула жазады:
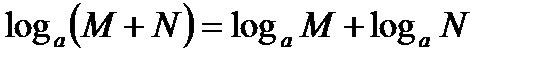
Мынадай қателіктер де жиі кездеседі.
| қ/с | Дұрысы | Қатесі |
| 1. | 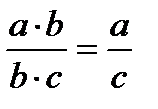 | 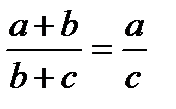 |
| 2. | 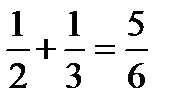 | 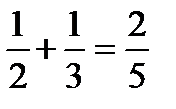 |
| 3. | 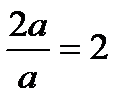 | 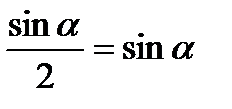 |
| 4. | 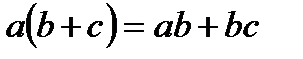 | 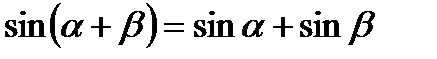 |
| 5. | 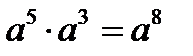 | 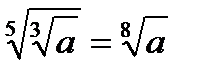 |
| 6. | 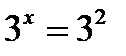 теңдеуінен, теңдеуінен, 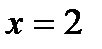 болады болады | 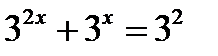 теңдеуінен, теңдеуінен, 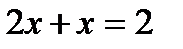 болады болады |
Мұғалім ол қателерді уақытында түзеп отыруы керек.
4. Модельдеу. Модельдеу – объектіні (түпнұсқаны), оның моделін (көшірмесін) жасау арқылы, ол көшірмені зерттейді. Объектінің көшірмесін жасағанда, сол объектінің зерттеушіні қызықтыратын белгілі бір жақтары сақталып қалады.
Жалпы алғанда модельдеу деп таным қызметінде бір жүйені – түпнұсқаны - онымен ұқсастық қатыста болатын жүйемен ауыстыратын, қандай да бір нақты (реальды) немесе ойша елестетілетін жүйе түсініледі. Модель арқылы түпнұсқа туралы мағлұматтар алуға болады. Модельдің айтарлықтай бір ерекшелігі оның түпнұсқамен сәйкестігінде (ұқсастығында). Бұл ұқсастық кеңістіктік, физикалық немесе функционалдық болуы мүмкін. Бірақ олар ұқсастықтың критерийі ретінде айқын тұжырымдалуы тиіс. Осы ұқсастық модельді зерттеу кезінде алынған нәтижелерді түпнұсқаға қайта көшіруге мүмкіндік береді.
Модельдер материалды және идеалды болуы ықтимал. Бірінші, болмысы жағынан табиғат заңдарына бағынатын табиғи объектілер болады. Екіншісі, дүниені сәйкес таңбалық пішінде (формада) бейнелейтін идеалдық құрылым болып, логикалық ойлау зандары бойынша өмір сүреді.
Кез келген “модельдік” зерттеудің мынадай құрылымы болады:
1) мәселені (есепті) қою;
2) модель құру немесе ол модельді таңдап алу;
3) модель зерттеу;
4) модель арқылы алынған білімдерді түп нұсқаға көшіру.
Мектептегі математика сабақтарында “модель” термині көбінесе тар мағынадағы, геометриялық фигураларды бейнелейтін ағаштан, шыныдан, сым темірден т.б. жасалған көрнекі құрал ретінде қолданылып жүр. Бірақ “модель” терминінің бұл мағынада қолданылуы, оның жалпы түсінігіне қайшы келмейді. Шынында да куб, пирамида және т.б. абстрактілі ұғымдардың әрқайсысы басқа бір абстрактілі ұғымдар арқылы анықталады. Геометриялық фигураны бейнелейтін нақтылы дене қандай заттан жасалғанына, кандай түске боялғанына қарамастан абстрактілі ұғымды сипаттайтын қасиеттерге ие болатындықтан, геометриялық фигуралардың моделі болып табылады.
Мектептегі математиканы оқыту үрдісінде нақтылы есептердің математикалық, дәлірек айтқанда логикалық-математикалық модельдерін құру жұмыстары да жүргізіледі. Бұл жағдайда есептің моделі есептің өзіне карағанда жоғары деңгейдегі абстракцияға сәйкес келеді. Нақтылы мазмұндағы әр түрлі есептердің бірдей логикалық-математикалық моделі болуы мүмкін.
Математика сабақтарында дәстүрлі калыптасқан теңдеу құру, белгісіздердің мүмкін мәндерін анықтау, белгісізді белгілеу т.б. терминдердің орнына жоғары сыныптарда есептің математикалық моделін кұру, есептің шартын логикалық-математикалық модель тіліне аудару және т.б. терминдерін пайдаланған тиімді. Әрине, бұл жерде қандай да бір жаңа термин енгізу жөнінде сөз болып отырған жоқ, мектеп математикасын оқыту барысында математиканың идеяларын біртіндеп енгізу мәселесі қозғалуда. Дұрыс игерілген терминдер бос сөз емес, олар ұғымдардың, идеялардың белгіленуі екендігін ұмытпағанымыз жөн.
Бұл мәселелерге оқушыларды дайындау үшін мектеп математика курсына арнайы жаңа тақырыптар енгізудің қажеті жоқ. Мектептің оқу материалында математикалық модельдеу элементтері жеткілікті, оқу үрдісінде оларды көрсетіп және түсіндіріп отыру керек.
Сұрақтар:
Математиканы оқытудың салыстыру әдісі.
Математиканы оқытудың анология әдісі.
1. Ә.Бидосов. Орта мектепте математиканы оқыту методикасы. – Алматы: Мектеп, 1989. – 224 б.
2.Әбілқасымова А.Е., Көбесов А.К., Рахымбек Д., Кенеш Ә С. Математиканы оқыту теориясы мен әдістемесі. – Алматы: Білім,1998. – 208 б.
3. Бейсеков Ж., Рахымбек Д., Шарипов Т.А. Орта мектепте математиканы оқыту әдістемесіне арналған оқу құралы. – Шымкент,2003. - 179 б
Лекция
Математиканы оқытудағы анализ және синтез
Жоспары:
1. Оқыту үдерісіндегі анализ және синтез
2. Элементтер анализ және синтез
3. Синтетикалық әдіс
4. Өрлей анализ әдісі
5. Ылдилай анализ әдісі
1. Оқыту үдерісіндегі анализ және синтез. Анализ деп бүтінді ойша немесе практикалық түрде құрамды бөліктерге бөліп, ол бөліктерді және олардың қасиеттері мен арақатынастарын жеке-жеке қарастыру арқылы зерттейтін әдіс түсініледі.
Синтез деп анализ арқылы бөлінген бөліктерді ойша немесе практикалық түрде біріктіру деп түсінеміз.
Қарапайым мағынада анализ бен синтезді былай түсінуге болады: егер бала велосипедті бөлшектеп, “шашып” тастаса, онда оның әрекеті анализ; ал егер ол сол бөлшектерден велосипедті қайта құрастырса, онда ол әрекеті синтез болып табылады.
Анализдеу үрдісінде күрделіден қарапайымға, бір түрліден еөп түрліге, нақтыдан абстрактілікке, белгісізден белгіліге салдардан салдарды туғызатын себепке қарай қозғалу жүзеге асырылса, синтезде бұл үрдістер керісінше жүреді. Математиканы оқыту процесінде бұл екі әдіс бірігіп, аналитикалық-синтетикалық әдіс ретінде қолданылады.
2. Элементтер анализ және синтез.Математикада элементар анализ бүтінді құрамды бөліктерге ажырату, ал элементар синтез сол құрамды бөліктерді қайтадан бүтінге жинақтау ретінде қолданылады.
Осы әдістердің қолданылу мысалдарын қарастырайық.
1) Ұғымдарды қалыптастыруда берілген ұғымды қамтитын жалпы қасиеттер көрсетіледі, одан соң ол қасиеттердің ішінен елеулілері бөлініп алынады, яғни элементар талдау жасалынады. Элементар синтез ұғымның елеулі қасиеттерін біріктіреді.
2) Барлық ғылымдар сияқты, математика да ұғымды жіктеуді пайдаланады. Тектік ұғымдарды түрлі ұғымдарға жіктеу, кейін түрлі ұғымдардың өзін басқа кластарға ажырату элементар талдау арқылы жүзеге асырылады. Мысалы, натурал сан ұғымын жіктеген кезде, натурал сан жиыны жай санға, құрама санға және бірліктерге жіктеледі.
Кеңістіктегі түзулердің өзара орналасуын ескеріп, оларды параллель, қиылысатын және айқас деп бөледі.
Функциялардың үзіліс нүктелерін жіктеу кезінде мынадай типтерге ажыратады: а) жөнделетін үзілісті нүкте; ә) бірінші шекті үзілісті нүкте; б) екінші текті үзілісті нүкте.
3) Көптеген математикалық сөйлемдерді дәлелдеу барысында оларды бірнеше бөліктерге ажыратуға тура келеді, яғни элементар талдау қолданылады.
Мысалы, косинустар теоремасын дәлелдеу үшін үшбұрыштың доғал, сүйір және тік болатын жағдайлары қарастырылады. Осы жағдайлардың бәрін біріктіру элементар синтез болып табылады.
Теоремаларды қарсы жору әдісімен дәлелдеу кезінде де элементар талдау пайдаланатынына оңай көз жеткізуге болады.
Мысалы, А=В екендігін көрсету үшін А≠В деп жориды. Нәтижеде дәлелдеп отырған теореманың шартына немесе аксиомаға немесе бұрын дәлелденген теоремаға қайшылық пайда болады. Үшіншінің болмайтындығы туралы заңға сәйкес, жоруымыз қате делінеді де, дәлелдеу керек ұйғарым дұрыс деп табылады. Демек, дәлелдеу кезінде А және В арасындағы мүмкін болатын барлық жағдайларға талдау жасалынады.
Салу есептерін шығарудағы зерттеу жүргізу элементар талдау болса, салуды орындау элементар синтез болып табылады.
4) Мектеп геометрия курсындағы кез келген аксиома элементар синтездің мысалы болады. «Бір түзудің бойында жатпайтын үш нүкте арқылы бір, тек бір ғана жазықтық жүргізуге болады» деген аксиомада элементар синтез жүзеге асырылып тұр, яғни алғашқы ұғымдар болып табылатын нүкте, түзу және жазықтықтың арасында қандай да бір байланыс тағайындалған.
3. Синтетикалық әдіс.Теоремаларды дәлелдеу кезінде теореманың шартынан оның қорытындысына қарай жүретін логикалық тізбектер құрылады. Теореманың қорытындысының дұрыстығы теореманың шартынан басталып, бұрыннан белгілі сөйлемдердің (аксиома, бұрын дәлелденген теорема т.б.) логикалық салдары ретінде тағайындалады. Дәлелдеудегі осындай әдіс синтетикалық әдіс деп аталады.
Мысалдар қарастырайық.
1-мысал. Теңсіздіктің дұрыстығын дәлелдеңдер 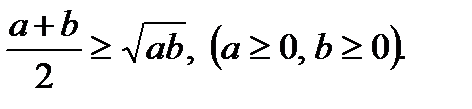 Бұл теңсіздіктің дұрыстығын синтетикалық әдіспен дәлелдеу үшін
Бұл теңсіздіктің дұрыстығын синтетикалық әдіспен дәлелдеу үшін 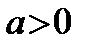 мен
мен 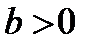 болғанда, дұрыстығы ақиқат мына теңсіздікті
болғанда, дұрыстығы ақиқат мына теңсіздікті 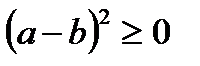 негізге аламыз.
негізге аламыз.
Оны мына түрде жазамыз:
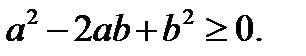

Теңсіздіктің екі жағына да бірдей 4ab-ны мүшелеп қоссақ.
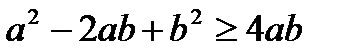 болады.
болады.
Енді соңғы теңсіздіктің екі жағынан бірдей квадрат түбір тапсақ:
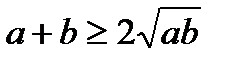 .
.
Осы теңсіздіктің екі жағында бірдей 2-ге мүшелеп бөлсек, онда дәлелденілуге тиісті төмендегі теңсіздік келіп шығады:
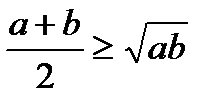 .
.
Сонымен, берілген теңсіздіктің дұрыстығы дәлелденді.
Тағы бір мысал қарастырайық.
2-мысал. Тік бұрышты үшбұрыштың гипотенузасының кубының катеттерінің кубтарының қосындысынан артық болатынын дәлелдеңдер.
Дәлелдеуі.Перпендикуляр мен көлбеудің негізгі қасиетіне сәйкес:
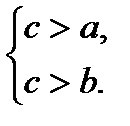
теңсіздектері орындалатындығы айқын. Осы теңсіздіктерді сәйкесінше 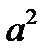 пен
пен 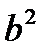 -қа мүшелеп көбейтіп, одан кейін екеуін мүшелеп қоссақ шығатыны
-қа мүшелеп көбейтіп, одан кейін екеуін мүшелеп қоссақ шығатыны
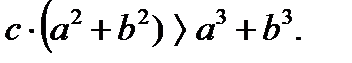
Ал, Пифагор теоремасы бойынша 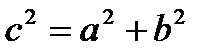 -қа тең болатындықтан, соңғы теңсіздікті былайша жазуға болады:
-қа тең болатындықтан, соңғы теңсіздікті былайша жазуға болады:
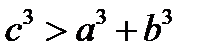
Сонымен, теңсіздіктің дұрыстығы дәлелденді.
Әрине, теңсіздікті дәлелдеу барысында түрлендірулердің не үшін жүргізіліп жатқанын оқушы бірден түсінбейді. Мектеп курсының көптеген теоремалары синтетикалық тәсілмен дәлелденген.
Синтетикалық әдіс мектеп математика курсын оқытуда кең түрде қолданылады.
4. Өрлей анализ әдісі.Бұл әдістің мәнін түсіну үшін мынадай мысал қарастырайық:
3-мысал. 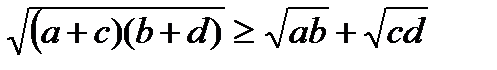 (1) теңсіздігін дәлелдеу керек, мұндағы a, b, c, d – оң сандар.
(1) теңсіздігін дәлелдеу керек, мұндағы a, b, c, d – оң сандар.
Дәлелдеуі. (1) теңсіздікті дәлелдеу үшін 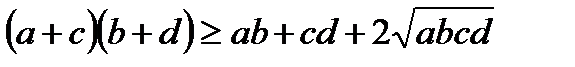 болатындығын көрсету жеткілікті немесе
болатындығын көрсету жеткілікті немесе 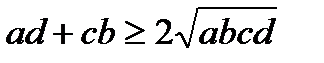 (2).
(2).
(2) теңсіздік мына теңсіздіктің салдары
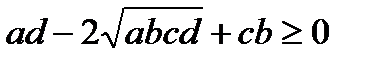
немесе
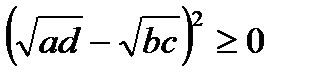 (3)
(3)
Сонымен (1) теңсіздік дәлелденді.
Қарастырылып отырған мысалдан өрлей анализ әдісі бойынша дәлелдеу қорытындыдан бастап жүргізілетінін көреміз.
Өрлей анализ әдісі бірінен соң бірін шешетін екі сұрақтың мәнін ашуға келеді.
1) Нені дәлелдеу керек;
2) Оны дәлелдеу үшін нені дәлелдеу жеткілікті.
Өрлей анализ әдісін пайдалануды меңгеру оқушылардың өз бетінше жұмыс істеуін жетілдіреді.
5. Ылдилай анализ әдісі.Ылдилай анализ әдісінің екі түрі бар: жетілмеген анализ және қарсы жору арқылы дәлелдеу.
Жетілмеген анализге мысал келтірейік.
4-мысал. n-нің кез келген натурал мәнінде мына теңсіздіктің дұрыстығын дәлелдеу керек.
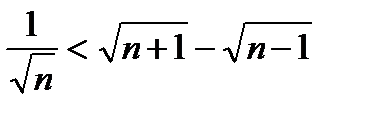 (1)
(1)
Дәлелдеуі. (1) теңсіздік орындалады деп жориық. Теңсіздіктің екі жағын 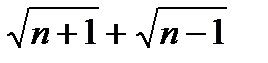 көбейткішіне көбейтейік. Түрлендірулер нәтижесі мынаны береді:
көбейткішіне көбейтейік. Түрлендірулер нәтижесі мынаны береді:
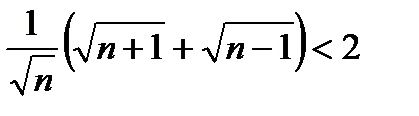 , (2)
, (2)
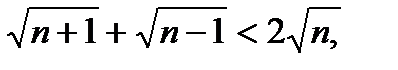 (3)
(3)
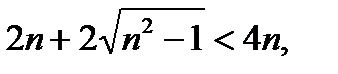 (4)
(4)
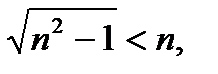 (5)
(5)
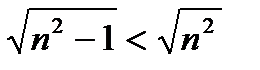 (6)
(6)
(6) теңсіздік айқын. Осымен талдау процесі аяқталады. Берілген теңсіздік пен айқын теңсіздік арасында қандай да бір байланыс тағайындалып тұр. Пайда болған теңсіздіктердің (1)-(6) тізбегі дәлелдеу бола алмайды. Толық дәлелдеу болу үшін (6)→(5)→(4)→(3)→(2)→(1) орындалатынын көрсету керек.
Қарсы жору әдісі математика курсында жиі қолданылады.
Бір мысал келтірейік.
5-есеп. а және b өзара жай сандар болса, онда 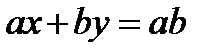 теңдеуінің натурал сандар жиынында шешімі болмайтынын дәлелдеу керек.
теңдеуінің натурал сандар жиынында шешімі болмайтынын дәлелдеу керек.
Дәлелдеуі. (x, y)-теңдеудің натурал шешімі болсын, онда 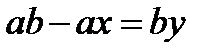 немесе
немесе 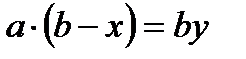 болады. Олай болса, by өрнегі а-ға бөлінеді, бірақ а және b өзара жай сандар, сондықтан у а-ға бөлінуі керек, яғни у=ka болады. Дәл осы сияқты х-тың да b-ға бөлінетінін көрсетуге болады, яғни x=mb. Бұл мәндерді берілген теңдікке қойсақ amb+bka=ab болып, бұдан m+k=1 болатындығы шығады. Бұл m және n натурал сандары үшін мүмкін емес. Мұндай қайшылық берілген ұйғарымның дұрыстығын дәлелдейді.
болады. Олай болса, by өрнегі а-ға бөлінеді, бірақ а және b өзара жай сандар, сондықтан у а-ға бөлінуі керек, яғни у=ka болады. Дәл осы сияқты х-тың да b-ға бөлінетінін көрсетуге болады, яғни x=mb. Бұл мәндерді берілген теңдікке қойсақ amb+bka=ab болып, бұдан m+k=1 болатындығы шығады. Бұл m және n натурал сандары үшін мүмкін емес. Мұндай қайшылық берілген ұйғарымның дұрыстығын дәлелдейді.
Бұл әдіспен дәлелдеудің алгоритмі мынадай:
1) дәлелденетін сөйлем жалған (дұрыс емес) деп алынып, оған қарама-қарсы ұйғарым дұрыс деп жорылады;
2) осының нәтижесінде әр түрлі жағдайлар белгіленеді;
3) әрбір жағдайдың салдарында теореманың шартына немесе бұдан тағайындалған сөйлемге қайшылыққа келеді;
4) қайшылықтың болуы біздің жоруымыздың дұрыс еместігін білдіреді;
5) дәлелденетін сөйлемнің қорытындысы дұрыс екен делінеді. Дәлелдеуді осы жоспар бойынша жүргізу оқушылардың қарсы жору арқылы дәлелдеу дағдыларын қалыптастырып, оның мәнін түсінуге мүмкіндік береді.
Сұрақтар:
1. Оқыту үдерісіндегі анализ және синтез
2. Элементтер анализ және синтез
3. Синтетикалық әдіс
4. Өрлей анализ әдісі
5. Ылдилай анализ әдісі
Әдебиеттер:
1. Ә.Бидосов. Орта мектепте математиканы оқыту методикасы. – Алматы: Мектеп, 1989. – 224 б.
2.Әбілқасымова А.Е., Көбесов А.К., Рахымбек Д., Кенеш Ә С. Математиканы оқыту теориясы мен әдістемесі. – Алматы: Білім,1998. – 208 б.
3. Бейсеков Ж., Рахымбек Д., Шарипов Т.А. Орта мектепте математиканы оқыту әдістемесіне арналған оқу құралы. – Шымкент,2003. - 179 б
