Метод відокремлення змінних
На відміну від прямокутних областей, для запису математичних моделей стаціонарних процесів у кругових областях (внутрішність або зовнішність круга, кільце, круговий сектор, криволінійний прямокутник) використовують
полярні координати. Проте методи інтеґрування крайових задач для рівнянь еліптичного типу у випадку кругових областей аналоґічні методам знаходження розв’язків змішаних задач для рівнянь гіперболічного та параболічного типів (при цьому роль початкових умов грають крайові умови на криволінійних краях, тобто при 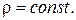 У внутрішніх задачах для круга та сектора необхідно враховувати додатково умову визначеності розв’язку в нулі:
У внутрішніх задачах для круга та сектора необхідно враховувати додатково умову визначеності розв’язку в нулі: 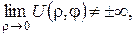 а
а
- 57 -
у зовнішніх задачах – умову реґулярності на нескінченості на площині: 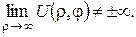 Крім того, для круга та кільця розв’язок повинен бути періодичною функцією з періодом 2π.
Крім того, для круга та кільця розв’язок повинен бути періодичною функцією з періодом 2π.
ПРИКЛАД 1.Знайти стаціонарний розподіл температури всередині пластинки, яка має форму кругового сектора 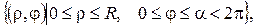 якщо прямолінійні краї пластинки теплоізольовані, а на дузі підтримується температура
якщо прямолінійні краї пластинки теплоізольовані, а на дузі підтримується температура 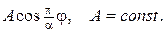
Розв’язання. Маємо наступну задачу:
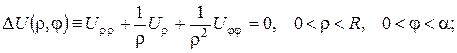 (15)
(15)
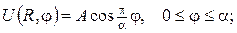 (16)
(16)
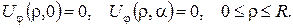 (17)
(17)
Крайові умови узгоджені, тому для знаходження розв’язку однорідного рівняння (15) застосовний метод відокремлення змінних (метод Фур’є). Отже, шукаємо 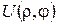 у вигляді
у вигляді
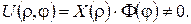
Відокремивши змінні у рівнянні (15) та у крайових умовах (17), одержимо:
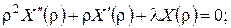 (18)
(18)
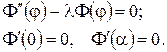 (19)
(19)
Із ЗШЛ (19) маємо:
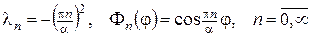
(нуль теж є власним значенням). Підставимо знайдені 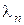 у (18) і визначимо
у (18) і визначимо 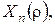 врахувавши умову визначеності розв’язку в нулі. Одержимо:
врахувавши умову визначеності розв’язку в нулі. Одержимо:
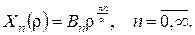
Таким чином, розв’язок рівняння Лапласа (15) матиме вигляд
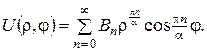 (20)
(20)
Сталі 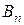 визначаємо підстановкою ряду (20) у крайову умову (16). Маємо:
визначаємо підстановкою ряду (20) у крайову умову (16). Маємо:
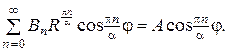
Звідси
- 58 -
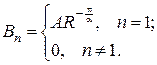
Отже, розв’язком задачі (15)-(17) буде функція
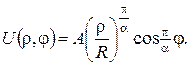
Зауваження. Рівняння Ейлера (18) інтеґрується зведенням до лінійного рівняння зі сталими коефіцієнтами заміною незалежної змінної 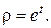 У випадку однорідного рівняння Ейлера можна застосовувати і простішу підстановку
У випадку однорідного рівняння Ейлера можна застосовувати і простішу підстановку 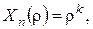 де
де 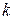 – невідома стала.
– невідома стала.
ПРИКЛАД 2. Проінтеґрувати крайову задачу та дати фізичну інтерпретацію:
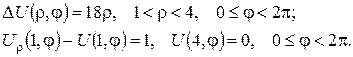
Фізична інтерпретація:
а) знайти положення рівноваги мембрани, яка має форму кільця, обмеженого колами 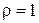 та
та 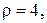 зовнішній край якої закріплений нерухомо, а внутрішній – пружно, причому край закріплення пружини зміщений; мембрана піддається дії зовнішньої сили інтенсивності
зовнішній край якої закріплений нерухомо, а внутрішній – пружно, причому край закріплення пружини зміщений; мембрана піддається дії зовнішньої сили інтенсивності 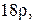 – або:
– або:
б) знайти стаціонарний розподіл температури всередині однорідної пластинки, яка має форму кільця, обмеженого колами 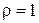 та
та 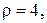 зовнішній край якої підтримується при нульовій температурі, якщо на внутрішньому краї проходить теплообмін із навколишнім середовищем сталої температури, а інтенсивність внутрішніх джерел тепла рівна
зовнішній край якої підтримується при нульовій температурі, якщо на внутрішньому краї проходить теплообмін із навколишнім середовищем сталої температури, а інтенсивність внутрішніх джерел тепла рівна 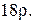
Розв’язання.
Перший спосіб (метод відокремлення змінних). Спочатку для спрощення задачі зведемо рівняння до однорідного підстановкою
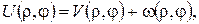
де 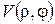 – нова невідома функція, а
– нова невідома функція, а 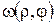 – деякий частинний розв’язок рівняння
– деякий частинний розв’язок рівняння
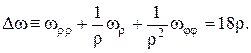
Будемо шукати допоміжну функцію у вигляді 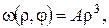 тоді з рівняння визначаємо
тоді з рівняння визначаємо 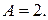 Отже, беремо
Отже, беремо 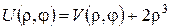 і для нової невідомої функції
і для нової невідомої функції 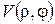 одержуємо наступну крайову задачу:
одержуємо наступну крайову задачу:
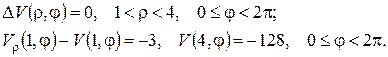
- 59 -
Застосовуючи до цієї задачі класичний метод відокремлення змінних, тобто шукаючи розв’язок у вигляді 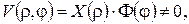 одержимо загальний розв’язок рівняння Лапласа у вигляді (див. [9], стор. 67-69):
одержимо загальний розв’язок рівняння Лапласа у вигляді (див. [9], стор. 67-69):
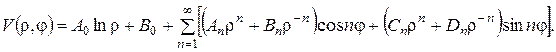 (21)
(21)
Підставивши ряд (21) у крайові умови для 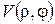 , одержимо:
, одержимо:
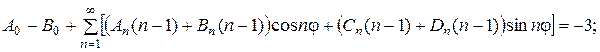
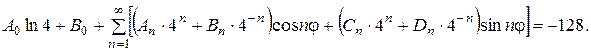
Звідси:
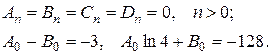
Із останньої системи 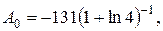
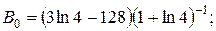 отже,
отже,
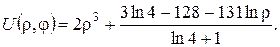 (22)
(22)
Другий спосіб (метод спуску). Поскільки вільний член у рівнянні Пуассона і крайові умови не залежать від полярного кута, то можна покласти 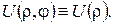 Тоді для визначення розв’язку матимемо крайову задачу для звичайного диференціального рівняння:
Тоді для визначення розв’язку матимемо крайову задачу для звичайного диференціального рівняння:
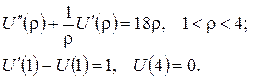
Проінтеґрувавши рівняння за допомогою підстановки 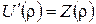 або шляхом виділення повної похідної, одержимо загальний розв’язок
або шляхом виділення повної похідної, одержимо загальний розв’язок
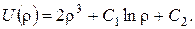
Визначивши сталі С1, С2 з крайових умов, дістанемо розв’язок крайової задачі у вигляді (22).
ПРИКЛАД 3. Побудувати розв’язок крайової задачі:
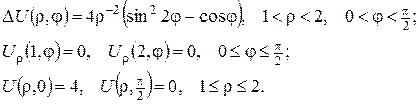
Розв’язання. Якщо проводити аналоґію зі змішаними задачами для рівнянь параболічного типу, то можна було б сказати, що маємо задачу типу 3
- 60 -
(крайові умови на прямолінійних краях заданого кільцевого сектора неоднорідні). Тому й етапи знаходження розв’язку в цих задачах аналоґічні.
Перший етап. Зводимо до однорідних крайові умови на прямолінійних краях підстановкою 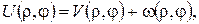 де
де 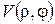 – нова невідома функція, а
– нова невідома функція, а 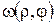 – допоміжна функція, котра повинна справджувати крайові умови
– допоміжна функція, котра повинна справджувати крайові умови
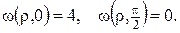
Будемо шукати допоміжну функцію 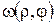 в періодичному вигляді
в періодичному вигляді
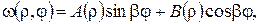
де невідомі функції 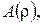
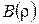 та стала β визначаються з крайових умов:
та стала β визначаються з крайових умов:
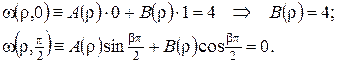
Остання умова виконується, наприклад, при 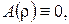 β=1. Отже, беремо
β=1. Отже, беремо 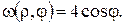 Тоді
Тоді 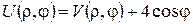 , а для
, а для 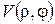 матимемо наступну крайову задачу:
матимемо наступну крайову задачу:
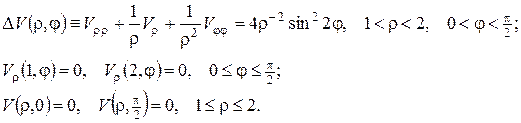
Другий етап. Шукаємо власні функції задачі Штурма-Ліувілля для відповідної однорідної задачі. Поклавши 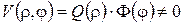 і відокремивши змінні у відповідному однорідному рівнянні та у крайових умовах на прямолінійних краях, одержимо ЗШЛ
і відокремивши змінні у відповідному однорідному рівнянні та у крайових умовах на прямолінійних краях, одержимо ЗШЛ
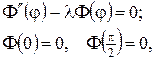
звідки 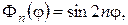
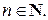
Третій етап. Розв’язок неоднорідної задачі шукаємо у вигляді ряду по знайдених власних функціях:
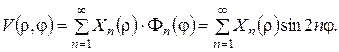
Невідомі коефіцієнти 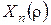 знаходимо підстановкою цього ряду в неоднорідне рівняння та у крайові умови на дугах. Одержимо:
знаходимо підстановкою цього ряду в неоднорідне рівняння та у крайові умови на дугах. Одержимо:
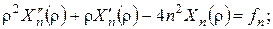 (23)
(23)
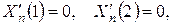
де коефіцієнт Фур’є
- 61 -
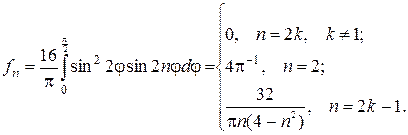
Ввівши підстановку 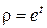 у рівняння Ейлера (23) і проінтеґрувавши його, будемо мати:
у рівняння Ейлера (23) і проінтеґрувавши його, будемо мати:
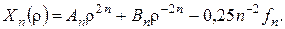
Із крайових умов 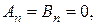 отже,
отже,

Завдання. Розв’язати крайову задачу прикладу 3, використовуючи метод спуску (див. приклад 2).
ПРИКЛАД 4. Знайти положення рівноваги однорідної мембрани, яка має форму кільця, обмеженого колами 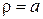 та
та 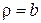
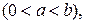 внутрішній край якої жорстко закріплений, а зовнішній вільний, якщо мембрана піддається дії зовнішньої сили інтенсивності
внутрішній край якої жорстко закріплений, а зовнішній вільний, якщо мембрана піддається дії зовнішньої сили інтенсивності 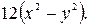 Початок координат знаходиться у центрі кільця.
Початок координат знаходиться у центрі кільця.
Розв’язання. Математична модель задачі (у полярній системі координат):
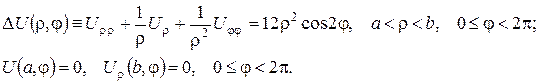
Розв’язок будемо шукати у вигляді 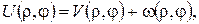 де
де 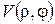 – нова невідома функція, а
– нова невідома функція, а 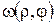 – деякий розв’язок заданого рівняння Пуассона. Зокрема, в даному випадку
– деякий розв’язок заданого рівняння Пуассона. Зокрема, в даному випадку 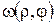 можна шукати у вигляді
можна шукати у вигляді 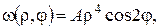 тоді з рівняння визначаємо
тоді з рівняння визначаємо 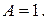 Отже,
Отже,
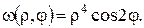
Тоді для 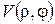 одержуємо крайову задачу (задля зручності домножимо рівняння на
одержуємо крайову задачу (задля зручності домножимо рівняння на 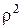 ):
):
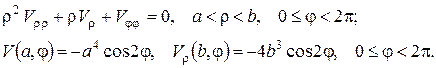
Застосовуючи до цієї задачі класичний метод відокремлення змінних, тобто шукаючи розв’язок у вигляді 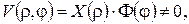 одержимо загальний розв’язок рівняння Лапласа у вигляді (див. приклад 2):
одержимо загальний розв’язок рівняння Лапласа у вигляді (див. приклад 2):
- 62 -
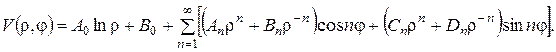
Коефіцієнти ряду слід визначати підстановкою ряду в крайові умови на колах, подаючи при цьому праві частини рівностей у вигляді ряду Фур’є. Проте в даному випадку функції крайових умов уже подані у вигляді розкладу в ряд Фур’є (резонансний випадок). Тому, одразу прирівнявши коефіцієнти при однакових власних функціях, одержимо: 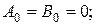
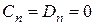 для всіх п; а
для всіх п; а 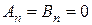 для всіх п, окрім п=2. При п=2 ж матимемо систему для визначення А2 та В2:
для всіх п, окрім п=2. При п=2 ж матимемо систему для визначення А2 та В2:
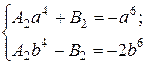
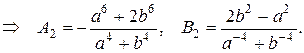
Отже, шуканий розв’язок крайової задачі запишеться у вигляді:
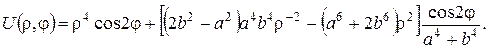
Інтеґрал Пуассона. Розв’язок внутрішньої задачі Діріхле для рівняння Лапласа в крузі радіуса R із центром у початку координат
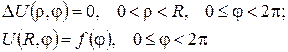
дається інтеґралом Пуассона
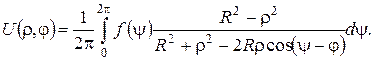
Для відповідної зовнішньої задачі ( 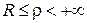 )
)
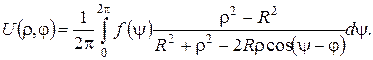
Вираз
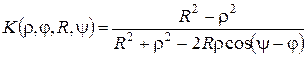
називається ядром Пуассона.
Задача Неймана. Умова стаціонарності теплового поля у випадку задачі Неймана для рівняння Лапласа в кругових областях має вигляд:
а) для внутрішності ( 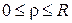 ) або зовнішності (
) або зовнішності ( 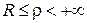 ) круга
) круга
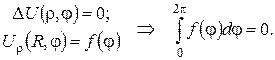
- 63 -
Для кругового сектора ( 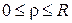 ,
, 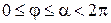 ), якщо крайові умови на прямолінійних краях однорідні, буде
), якщо крайові умови на прямолінійних краях однорідні, буде 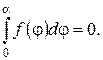
б) для кільця ( 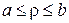 ,
, 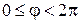 )
)
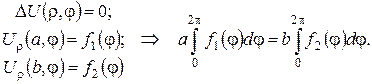
Для криволінійного прямокутника чи кільцевого сектора ( 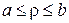 ,
, 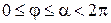 ), якщо крайові умови на прямолінійних краях однорідні, буде
), якщо крайові умови на прямолінійних краях однорідні, буде
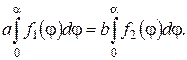
Якщо наведені вище умови виконуються, то задача Неймана буде мати розв’язок, який визначається з точністю до сталого доданка. Якщо ж рівняння неоднорідне або ж при 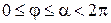 маємо неоднорідні крайові умови на прямолінійних краях, то можна спробувати звести задачу до однорідної з урахуванням умов узгодженості аналоґічно до прямокутних областей (див. приклад 6 попереднього розділу).
маємо неоднорідні крайові умови на прямолінійних краях, то можна спробувати звести задачу до однорідної з урахуванням умов узгодженості аналоґічно до прямокутних областей (див. приклад 6 попереднього розділу).
