Парная линейная регрессионная модель

Липецкий государственный технический университет

Заочный факультет

Кафедра электропривода

РЕФЕРАТ

По теории экспериментов

Регрессионный анализ.

Оценка параметров линейных регрессионных моделей.

Студент _____________________ Истомин Н.С.

Группа ЗМ-ЭО-16-1

Руководитель

к.т.н., доцент _____________________ Шишлин Д.И.

Липецк 2017 г.

Оглавление

1. Уравнение регрессии…………………….…..……………..…………3

2. Парная линейная регрессионная модель..........................................4

Список источников ……………….……………………………………..17

Уравнение регрессии

Основная цель регрессионного анализа состоит в определении связи между некоторой характеристикой Y наблюдаемого явления или объекта и величинами х₁, х₂, …, х_n, которые обусловливают, объясняют изменения Y. Переменная Y называется зависимой переменной (откликом), влияющие переменные х₁, х₂, …, х_n называются факторами (регрессорами). Установление формы зависимости, подбор модели (уравнения) регрессии и оценка ее параметров являются задачами регрессионного анализа.

В регрессионном анализе изучаются модели вида Y = φ(X) + ε, где Y - результирующий признак (отклик, случайная зависимая переменная); X – фактор (неслучайная независимая переменная); ε – случайная переменная, характеризующая отклонение фактора Х от линии регрессии (остаточная переменная). Уравнение регрессии записывается в виде: y_x = φ(x, b₀, b₁, …, b_p), где х – значения величины Х; y_x = M_х(Y); b₀, b₁, …, b_p – параметры функции регрессии φ. Таким образом, задача регрессионного анализа состоит в определении функции и ее параметров и последующего статистического исследования уравнения.

В зависимости от типа выбранного уравнения различают линейную и нелинейную регрессию (в последнем случае возможно дальнейшее уточнение: квадратичная, экспоненциальная, логарифмическая и т.д.). В зависимости от числа взаимосвязанных признаков различают парную и множественную регрессию. Если исследуется связь между двумя признаками (результативным и факторным), то регрессия называется парной, если между тремя и более признаками – множественной (многофакторной) регрессией.

На первом этапе регрессионного анализа данные наблюдений или эксперимента представляют графически.

Зависимость между переменными Х и Y изображают точками на координатной плоскости (х, y) и соединяют их ломаной линией. Этот ломаный график называется эмпирической линией регрессии Y по Х. По виду эмпирической линии регрессии делают предположение о виде (форме) зависимости переменной Y от Х.

Если вид функции φ в уравнении регрессии выбран, то для оценки неизвестных параметров b₀, b₁, …, b_p используется метод наименьших квадратов (МНК). Согласно методу неизвестные параметры функции выбираются таким образом, чтобы сумма квадратов отклонений экспериментальных (эмпирических) значений y_i от их расчетных (теоретических) значений была минимальной, т.е.

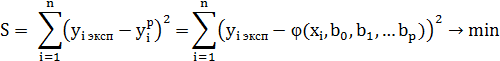
где 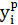– значение, вычисленное по уравнению регрессии; 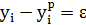– отклонение (ошибка, остаток); n – количество пар исходных данных.

Парная линейная регрессионная модель

Рассмотрим парную линейную регрессионную модель взаимосвязи двух переменных, для которой функция регрессии φ(х) линейна. Обозначим через y_x условную среднюю признака Y в генеральной совокупности при фиксированном значении x переменной Х. Тогда уравнение регрессии будет иметь вид:

y_x = ax + b, где a – коэффициент регрессии (показатель наклона линии линейной регрессии). Коэффициент регрессии показывает, на сколько единиц в среднем изменяется переменная Y при изменении переменной Х на одну единицу. С помощью метода наименьших квадратов получают формулы, по которым можно вычислять параметры линейной регрессии, представленные в таблице 1.

Таблица 1. Формулы для расчета параметров линейной регрессии

Свободный член b	Коэффициент регрессии a	Коэффициент детерминации
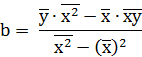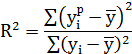Проверка гипотезы о значимости уравнения регрессии
Н0:	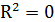Н1: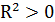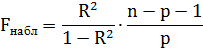
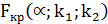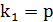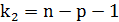, , , (для линейной регрессии р = 1)

Направление связи между переменными определяется на основании знака коэффициента регрессии. Если знак при коэффициенте регрессии положительный, связь зависимой переменной с независимой будет положительной. Если знак при коэффициенте регрессии отрицательный, связь зависимой переменной с независимой является отрицательной (обратной).

Для анализа общего качества уравнения регрессии используют коэффициент детерминации R², называемый также квадратом коэффициента множественной корреляции. Коэффициент детерминации (мера определенности) всегда находится в пределах интервала [0;1]. Если значение R² близко к единице, это означает, что построенная модель объясняет почти всю изменчивость соответствующих переменных. И наоборот, значение R² близкое к нулю, означает плохое качество построенной модели.

Коэффициент детерминации R² показывает, на сколько процентов 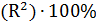найденная функция регрессии описывает связь между исходными значениями Y и Х. Соответственно, величина 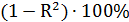показывает, сколько процентов вариации параметра Y обусловлены факторами, не включенными в регрессионную модель.

При высоком значении коэффициента детерминации 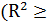75%) можно делать прогноз 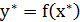для конкретного значения 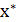в пределах диапазона исходных данных. При прогнозах значений, не входящих в диапазон исходных данных, справедливость полученной модели гарантировать нельзя. Это объясняется тем, что может проявиться влияние новых факторов, которые модель не учитывает.

Оценка значимости уравнения регрессии осуществляется с помощью критерия Фишера. При условии справедливости нулевой гипотезы критерий имеет распределение Фишера с числом степеней свободы 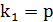, 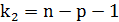(для парной линейной регрессии р = 1). Если нулевая гипотеза отклоняется, то уравнение регрессии считается статистически значимым. Если нулевая гипотеза не отклоняется, то признается статистическая незначимость или ненадежность уравнения регрессии.

Пример 1. В механическом цехе анализируется структура себестоимости продукции и доля покупных комплектующих. Было отмечено, что стоимость комплектующих зависит от времени их поставки. В качестве наиболее важного фактора, влияющего на время поставки, выбрано пройденное расстояние. Провести регрессионный анализ данных о поставках, приведенных в таблице 2.

Таблица 2. Данные о поставках

Расстояние, миль	3,5	2,4	4,9	4,2	3,0	1,3	1,0	3,0	1,5	4,1
Время, мин

Для проведения регрессионного анализа:

1. построить график исходных данных, приближенно определить характер зависимости;

2. выбрать вид функции регрессии и определить численные коэффициенты модели методом наименьших квадратов и направление связи;

3. оценить силу регрессионной зависимости с помощью коэффициента детерминации;

4. оценить значимость уравнения регрессии;

5. сделать прогноз (или вывод о невозможности прогнозирования) по принятой модели для расстояния 2 мили.

Решение:

1. На координатной плоскости построим точки с координатами {x_i, y_i}. Построенные точки не находятся точно на линии: помимо расстояния на время поставки влияют пробки на дорогах, время суток, дорожные работы, погода, квалификация водителя, вид транспорта. Но эти точки собраны вдоль прямой линии, поэтому можно предположить линейную положительную связь между параметрами.

2. Вычислим суммы, необходимые для расчета коэффициентов уравнения линейной регрессии и коэффициента детерминации R²:

Таблица 3. Расчет коэффициентов уравнения линейной регрессии

№
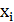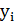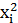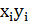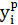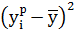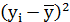	3,5			12,25	56,00		15,22	2,63	5,76
	2,4			5,76	31,20		12,30	1,70	0,36
	4,9			24,01	93,10		18,95	28,59	29,16
	4,2			17,64	75,60		17,09	12,15	19,36
	3,0			9,00	36,00		13,89	0,08	2,56
	1,3			1,69	14,30		9,37	17,88	6,76
	1,0			1,00	8,00		8,57	25,27	31,36
	3,0			9,00	42,00		13,89	0,09	0,16
	1,5			2,25	13,50		9,90	13,67	21,16
	4,1			16,81	65,60		16,82	10,36	5,76
Σ	28,9			99,41	435,30		–	112,42	122,40

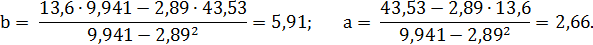
Искомая регрессионная зависимость имеет вид: 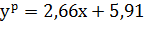. Определяем направление связи между переменными: знак коэффициента регрессии положительный, следовательно, связь также является положительной, что подтверждает графическое предположение.

3. Вычислим коэффициент детерминации: 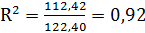или 92%. Таким образом, линейная модель объясняет 92% вариации времени поставки, что означает правильность выбора фактора (расстояния). Не объясняется 8% вариации времени, которые обусловлены остальными факторами, влияющими на время поставки, но не включенными в линейную модель регрессии.

4. Проверим значимость уравнения регрессии:

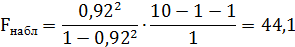
Т.к. 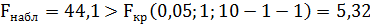– уравнение регрессии (линейной модели) статистически значимо.

5. Решим задачу прогнозирования. Поскольку коэффициент детерминации R² имеет достаточно высокое значение и расстояние 2 мили, для которого надо сделать прогноз, находится в пределах диапазона исходных данных, то можно сделать прогноз:

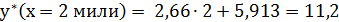мин.

Регрессионный анализ удобно проводить с помощью возможностей Excel. Режим работы "Регрессия" служит для расчета параметров уравнения линейной регрессии и проверки его адекватности исследуемому процессу. В диалоговом окне следует заполнить следующие параметры:

· Входной интервал Y - это диапазон данных по результативному признаку, он должен состоять из одного столбца.

· Входной интервал X - это диапазон ячеек, содержащих значения факторов (независимых переменных). Число входных диапазонов (столбцов) 16.

· Флажок Метки, устанавливается в том случае, если в первой строке диапазона стоит заголовок.

· Флажок Уровень надежности активизируется, если в поле, находящееся рядом с ним необходимо ввести уровень надежности, отличный от установленного по умолчанию (95%).

· Константа ноль. Данный флажок необходимо установить, если линия регрессии должна пройти через начало координат (b = 0).

· Флажки в группе Остатки и График остатков устанавливаются, если необходимо включить в выходной диапазон соответствующие столбцы или графики.

Пример 2. Выполнить задание примера 1 с помощью режима "Регрессия" Exсel.

Таблица 4. Результаты регрессионного анализа

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,958275757
R-квадрат	0,918292427
Нормированный R-квадрат	0,90807898
Стандартная ошибка	1,11809028
Наблюдения
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение
Y-пересечение	5,913462144	0,884389599	6,6864899	0,000155
Переменная X 1	2,65970168	0,280497238	9,4820958	1,26E-05

Рассмотрим представленные в таблице результаты регрессионного анализа.

Величина R-квадрат, называемая также мерой определенности, характеризует качество полученной регрессионной прямой. Это качество выражается степенью соответствия между исходными данными и регрессионной моделью (расчетными данными). В нашем примере мера определенности равна 0,91829, что говорит об очень хорошей подгонке регрессионной прямой к исходным данным и совпадает с коэффициентом детерминации R², вычисленным по формуле.

Множественный R - коэффициент множественной корреляции R - выражает степень зависимости независимых переменных (X) и зависимой переменной (Y) и равен квадратному корню из коэффициента детерминации. В простом линейном регрессионном анализе множественный коэффициент R равен линейному коэффициенту корреляции (r = 0,958).

Коэффициенты линейной модели: Y-пересечение выводит значение свободного члена b, а переменная Х1 – коэффициента регрессии а. Тогда уравнение линейной регрессии:

у = 2,6597x + 5,9135 (что хорошо согласуется с результатами расчета в примере 1).

Далее проверим значимость коэффициентов регрессии: a и b. Сравнивая попарно значения столбцов Коэффициенты и Стандартная ошибка в таблице, видим, что абсолютные значения коэффициентов больше, чем их стандартные ошибки. К тому же эти коэффициенты являются значимыми, о чем можно судить по значениям показателя Р-значение, которые меньше заданного уровня значимости α=0,05.

Таблица 5. Вывод остатков

Наблюдение	Предсказанное Y	Остатки	Стандартные остатки
	15,22241803	0,777581975	0,737641894
	12,29674618	0,703253823	0,667131568
	18,94600038	0,053999622	0,051225961
	17,0842092	0,915790799	0,868751695
	13,89256718	-1,892567185	-1,795356486
	9,371074328	1,628925672	1,545256778
	8,573163824	-0,573163824	-0,543723571
	13,89256718	0,107432815	0,101914586
	9,903014664	-0,903014664	-0,8566318
	16,81823903	-0,818239033	-0,776210624

В таблице представлены результаты вывода остатков. При помощи этой части отчета мы можем видеть отклонения каждой точки от построенной линии регрессии. Наибольшее абсолютное значение остатка в данном случае - 1,89256, наименьшее - 0,05399. Для лучшей интерпретации этих данных строят график исходных данных и построенной линией регрессии. Как видно из построения, линия регрессии хорошо "подогнана" под значения исходных данных, а отклонения носят случайный характер.

Список источников

1. Дрейпер Н., Смит Г. Прикладной регрессионный анализ: В 2-х кН. Кн. 1/ Пер. с англ. – 2-е изд., перераб. и доп. – М. : Финансы и статистика, 1986. 366 с., ил.

2. Гришенцев А. Ю. Теория и практика технического и технологического эксперимента./ Учебное пособие. – СПб: СПбГУ ИТМО, 2010. 102 с., ил.