Импеданс, кажущееся сопротивление и вектор Визе

Главной особенностью магнитотеллурических методов является то, что изменяющиеся параметры источника первичного поля неизвестны. Электрические и магнитные компоненты поля долгое время, до открытия нормировки поля в значения кажущегося сопротивления по входному импедансу, изучались по отдельности. Параметры среды определялись на качественном уровне путем измерения относительных изменений интенсивности отдельных компонент поля (главным образом, электрического) на соседних точках в предположении горизонтальной однородности первичного поля.

А. Н. Тихонов, как уже отмечалось во введении, первым, опираясь на пионерские работы М.А. Леонтовича по теории распространения электромагнитных волн на поверхности проводящего полупространства, предложил выход из этой ситуации путем измерения импеданса (impedance–сопротивление). Импеданс Z определялся как отношение горизонтальных сопряженных (взаимно-ортогональных) компонент электромагнитного поля E_x и H_y или E_y и H_x в единицах 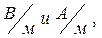соответственно, и имеет размерность Ом. На поверхности горизонтально-однородной n-слойной среды можно записать:

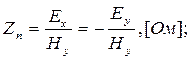или иначе 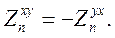(4.1)

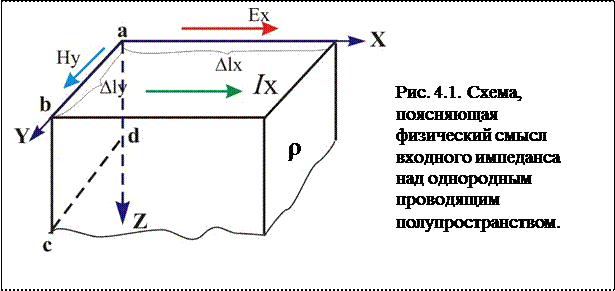
Пояснение физического смысла импеданса Z как полного

электрического сопротивления некоторого объема нижнего полупространства дано на рис 4.1.

Выберем в среде с удельным сопротивлением ρ воображаемый прямоугольный параллелепипед со сторонам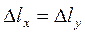и и 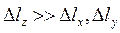. Напряженность поля 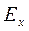на грани Х определяется как отношение падения потенциала 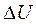на интервале пути 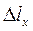к длине приемной линии , .

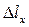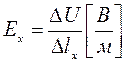Обратимся к первому закону Максвелла в квазистационарном приближении 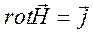и вычислим поток 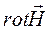через воображаемую поверхность S, охватывающую магнитный контур.

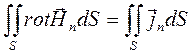
Применив теорему Стокса, найдем, что циркуляция магнитного поля по контуру abcd, охватывающему источник, равна силе полного тока проводимости в направлении оси Х (рис. 4.1).

.

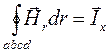Магнитные поля на вертикальных отрезках ad и bc на влияют на величину тока 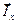, поскольку они находятся в продольной плоскости по отношению к току Вклад магнитного поля на отрезке cd ничтожно мал вследствие его удаленности на глубину. Таким образом циркуляция магнитного поля и, следовательно, сила тока приближенно равна произведению напряженности магнитного поля на длину отрезка ab. Можно записать 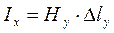и следовательно 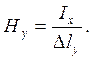Отсюда 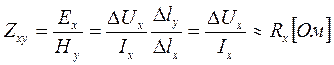, если принять, что 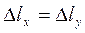. Таким образом импданс Z_xy приблизительно равен полному сопротивлению параллелепипеда 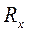в направлении координаты Х.

На поверхности n-слойного горизонтально-однородного полупространства результаты обработки наблюдений МТ поля по формуле 4.1 дают входной импеданс 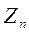. Горизонтальные компоненты поля 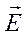и 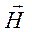одинаково и линейно зависят от параметров источника, при этом 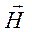зависит от параметров источника, тогда как электрические компоненты содержат информацию о нижнем полупространстве. Поэтому после деления их спектральных образов друг на друга вклад параметров источника сокращается и входной импеданс, согласно граничным условиям М.А. Леонтовича, содержит информацию только о параметрах нижнего полупространства.

МТ-АМТ поле, как было показано выше, изменяется в широком диапазоне частот (от 10^-5 до 10⁴ Гц). После проведения соответствующих процедур фильтрации это позволяет выполнять частотное индукционное зондирование, которое принято называть магнитотеллурическим зондированием (МТЗ).Импеданс является комплексным числом, поскольку электрические и магнитные компоненты поля сдвинуты между собой по фазе. Модуль импеданса над однородным полупространством, как это будет показано ниже, в разделе имеет вид:

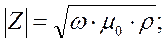(4.2)

Отсюда нетрудно определить удельное электрическое сопротивление нижнего полупространства

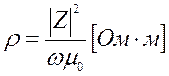(4.3)

В случае реальной неоднородной геологической среды удельное электрическое сопротивление, определенное по формуле (4.3), называется кажущимся и записывается в виде

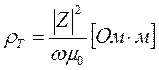(4.4)

Понятие кажущегося сопротивления в практику магнитотеллурической разведки впервые ввел Луи Каньяр. При этом он использовал практическую систему единиц, удобную для обработки результатов полевых наблюдений. Расстояние он предложил измерять в километрах (км), напряженность электрического поля Е – в милливольтах на километр (мВ/км), напряженность магнитного поля Н – в гаммах ( 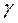). Отсюда импеданс в практических единицах, обозначим его Z^пр, он предложил измерять в единицах милливольт на гамма-километр ( 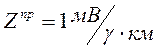). Магнитное поле напряженностью в 1 гамму представляет собой дольную единицу из системы СГСМ 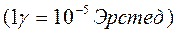. Одна гамма легко переводится из СГСМ в систему СИ с помощью соотношения 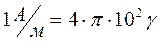, где 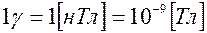. Кажущееся сопротивление в этом случае определяется путем подстановки в выражение (4.4) принятых выше дольных единиц - 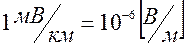и 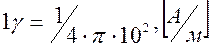. Принимая во внимание, что 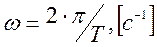, , 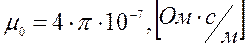получим

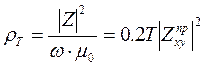, [Ом∙м], (4.5)

где .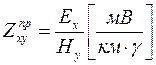

Определение кажущегося сопротивления МТ-поля по формуле (4.5), впервые введенное Луи Каньяром в 1952 году, получило на многие годы всеобщее признание. В этом выражении соединились единицы систем СИ и СГСМ. Однако, эта ситуация не могла продолжаться долго. В 1973 году Международная ассоциация по геомагнетизму и аэрономии (МАГА) в специальной Резолюции № 3 рекомендовала всем геофизикам пользоваться только системой единиц СИ в качестве единого стандарта. Следуя этому требованию, в выражении для импеданса в формуле (4.5) необходимо использовать величину магнитной индукции 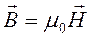, поскольку одна гамма численно равна одной нанотесле, то есть дольной единице магнитной индукции 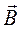. В этом случае импеданс утрачивает размерность комплексного сопротивления и приобретает размерность скорости, мы его обозначим как

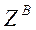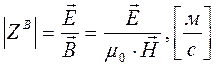. (4.6)

Подставив в (4.5) новое определение 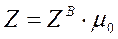из (4.6), получим выражение кажущегося сопротивления в следующем виде

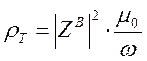(4.7)

Приведенная выше формула для вычисления кажущегося удельного электрического сопротивления (4.7) и само определение импеданса в единицах скорости находятся в противоречии с традициями магнитотеллурики, заложенными А.Н. Тихоновым и Л. Каньяром. Поэтому, по рекомендации М. Н. Бердичевского и В.И. Дмитриева, принято сохранить прежнее значение импеданса как комплексного сопротивления, определяемого отношением ортогональных компонент напряженности электрического поля 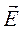и магнитного поля 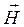. Но при этом из обращения изъята внесистемная единица «гамма». Вместо нее принято использовать дольную единицу из системы СИ, близкую по величине к единице гамма. В качестве такой величины принята одна тысячная доля ампера на метр,

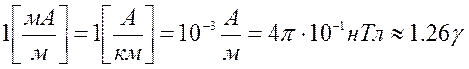
Импеданс при этом измеряется в 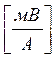. Подставив в выражение (4.4) поправочный множитель 10^-3, получим новое, теперь уже общепринятое выражение для расчета кажущегося сопротивления в системе СИ.

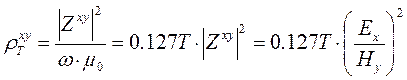(4.8)

В выражении (4.8) значение кажущегося сопротивления определяется по измеренным в поле значениям напряженности электрического поля Е_х в милливольтах на километр 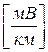и напряженности магнитного поля Н_y в миллиамперах на метр .

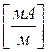Помимо кажущегося сопротивления, вычисляемого по входному импедансу, в магнитотеллурике применяются другие виды нормировок: в виде отношения напряженностей одноименных компонент электрического или магнитного поля на полевой (передвижной) и базовой (опорной) точках, в виде отношения вертикальной и горизонтальной компонент магнитного поля. Эти и ряд других приемов лежат в основе многочисленных модификаций МТ-методов. Среди них в качестве основных следует отметить метод теллурических токов (ТТ), основанный на измерении отношения электрических компонент магнитотеллурического поля на передвижной (полевой) и закрепленной (базовой) точках и метод магнитовариационного профилирования (МВП), основанный на измерении отношения вертикальной составляющей магнитного поля к полному горизонтальному магнитному вектору путем решения уравнения

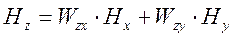(4.9)

Равенство (4.9) носит название соотношения Визе-Паркинсона. На основе измерения значений всех трех компонент магнитного поля 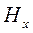, , 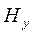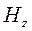устанавливаются линейные связи между вертикальным полем 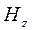и горизонтальными компонентами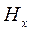 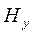, а затем находится индукционный комплексный вектор Визе-Паркинсона 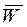, изображаемый в виде стрелок (типперов), ориентированных вкрест простирания двумерно-неоднородных структур.

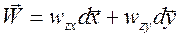(4.10)

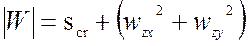
Метод МВП может быть реализован как по измерениям в одной точке, так и путем измерения поля на передвижной точке относительно базовой точки (reference point).

Все методы отношений основаны на изучении линейных связей между различными компонентами поля. Такие связи являются частотно-зависимыми и поэтому могут рассматриваться как передаточные функции среды. Причем среды только горизонтально-неоднородной, поскольку существование вертикальной компоненты магнитного поля H_z и горизонтальных производных любых компонент поля возможно только в условиях горизонтальных изменений сопротивления среды, если источник поля заведомо однороден, то есть находится достаточно далеко от точки наблюдения по сравнению с длиной электромагнитной волны в земле.

В последующем описании мы остановимся, главным образом, на рассмотрении метода магнитотеллурического зондирования (МТЗ), являющегося базовым методом магнитотеллурической разведки, выполняемой в рамках модели Тихонова-Каньяра.

Модель Тихонова-Каньяра.

Практическое применение магнитотеллурических методов исследования земных недр стало возможным после создания российским геофизиком, математиком академиком А.Н. Тихоновым и французским геофизиком Л. Каньяром модели, адекватно описывающей реальные электромагнитные процессы в Земле в рамках определенных ограничений. Эта модель, получившая название модели Тихонова-Каньяра, основана на следующих четырех положениях (постулатах).

Первый постулат. Возбуждение вторичного электромагнитного поля в Земле происходит исключительно за счет индукционного воздействия переменных токов, протекающих в ионосфере и магнитосфере. Это означает, что можно пренебречь гальваническими утечками, возникающими за счет вертикальных токов, протекающих из ионосферы в Землю через атмосферу. Приближенная модель электропроводности волновода «ионосфера-атмосфера-Земля», в котором формируется магнитотеллурическое поле, представлена ниже в таблице 5.1.

Таблица 5.1.

Приближенная модель электропроводности волновода

«Земля - ионосфера»

«Слой»	Удельное электрическое сопротивление, Ом·м	Мощность, км
Ионосфера	104 , днем
105 , ночью
Атмосфера	1014 , при Т=1час
1010 , при Т=1с
Земля	104	∞

Можно видеть, что контраст по сопротивлению между атмосферой и Землей достигает 5-10 порядков. В этих условиях магнитосферный ток будет замыкаться на ионосфере, и лишь совершенно ничтожная его часть будет замыкаться на Землю, пройдя гальваническим путем через плохо проводящую атмосферу. Доказательство этого положения, несмотря на его кажущуюся очевидность, потребовало многолетних дискуссий между школой М.Н. Бердичевского, Л.Л. Ваньяна и В.И. Дмитриева, с одной стороны, и школой Д.Н. Четаева, с другой стороны.

Заметим, что удельное сопротивление атмосферы является комплексной величиной и зависит от периода вариаций (таблица 5.1.). Это обусловлено тем, что вследствие высокого сопротивления воздуха поле выходит за рамки квазистационарного приближения, и на его параметры оказывают влияние токи смещения.

Второй постулат. Линейные размеры исследуемого пространства L много меньше радиуса Земли R (L<<R). Это положение означает, что магнитотеллурическое зондирование выполняется в достаточно локальной области (в пределах первой тысячи километров), где можно пренебречь сферичностью Земли и считать дневную поверхность плоской.

Третий постулат. Третий постулат непосредственно вытекает из второго. В модели Тихонова-Каньяра Земля характеризуется горизонтально-слоистым одномерным разрезом. Удельное сопротивление является функцией только одной, вертикальной координаты z: ρ=ρ(z). Тангенциальные производные сопротивления тождественно равны нулю.

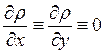
Четвертый постулат.Источник находится далеко от точки наблюдения, на расстоянии r, много большем длины волны в земле λ (r>>λ). Длина электромагнитной волны в земле 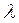зависит от периода вариаций Т, [c]и удельного электрического сопротивления нижнего полупространства 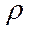, [Ом·м] и определяется численным, то есть лишенным физической размерности выражением, вытекающим из анализа уравнений Максвелла в квазистационарном приближении [Жданов, 1986].

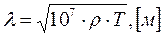(5.1)

Этот постулат означает, что первичная часть МТ-поля (излучение ионосферы) в точке наблюдения не должно иметь горизонтальных производных и представлять собой плоскую по отношению к поверхности Земли электромагнитную волну, распространяющуюся сверху вниз. Заметим, что применение понятия «волна» и «длина волны» к магнитотеллурическому полю является лишь удобной абстракцией, применимой к проводящему нижнему полупространству. В верхнем полупространстве длины «волн», применяемых в МТЗ, превышают в сотни и тысячи раз диаметр Земли.