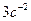Относительное нормальное ускорение
ar n = v2r / 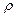 = 0,
= 0,
так как траектория относительного движения — прямая (ρ=∞).
Модуль переносного вращательного ускорения
| aBe= Rεe , | (2) |
где εe = | 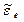 | - модуль углового ускорения тела D:
| - модуль углового ускорения тела D: 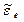 = d2φe/dt2 = 1,8–54t,
= d2φe/dt2 = 1,8–54t,
При t = 2/9 с 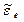 = -10,2 рад/с2;
= -10,2 рад/с2; 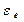 = 10,2 рад/с2.
= 10,2 рад/с2.
Знаки 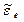 и
и 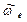 одинаковы; следовательно, вращение треугольника D ускоренное, направления векторов
одинаковы; следовательно, вращение треугольника D ускоренное, направления векторов 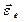 и
и 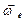 совпадают (рис. 30, a, б). Согласно (2),
совпадают (рис. 30, a, б). Согласно (2),
aBe = 102 см/с2. Вектор 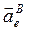 направлен в ту же сторону, что и
направлен в ту же сторону, что и 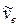 .
.
Модуль переносного центростремительного ускорения аЦе=Rω2e или аЦе = 9 см/с2.
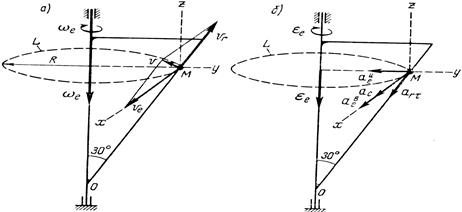 |
| Рис. 30. |
Вектор 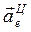 направлен к центру окружности L. Кориолисово ускорение
направлен к центру окружности L. Кориолисово ускорение
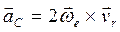 .
.
Модуль кориолисова ускорения
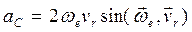
где
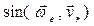 =sin 150° = –0,5.
=sin 150° = –0,5.
С учетом найденных выше значений ωе и vr получаем
aС = 61 см/с2.
Вектор 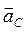 направлен согласно правилу векторного произведения (рис. 30, б).
направлен согласно правилу векторного произведения (рис. 30, б).
Модуль абсолютного ускорения точки М находим способом проекций:
aх = aBe+ас; ау = – аЦе – arτ cos 60°;
аz = – arτ cos 30°; 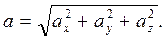
Результаты расчета сведены в табл. 11,
Таблица 11
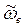 , рад/с. , рад/с. | Скорость, см/с | 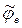 , рад/с2 , рад/с2 | Ускорение, см/с2 | ||||||||||
| ve | 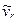 | v | aeц | aeВ | arn | 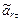 | aC | ax | ay | az | a | ||
| -0,93 | 9,3 | 65,2 | 65,9 | -10,2 | -355 | -186 |
ФГОУ ВПО
Красноярский Государственный Аграрный Университет
Методические указания к выполнению курсовой работы по теоретической механике.
Раздел «Динамика»
Красноярск 2004г.
Зотов А.В. Методические указания к выполнению курсовой работы по теоретической механике. Раздел «Динамика»
Рецензенты:
Печатается по решению редакционно-издательского отдела КрасГАУ.
Введение.
Методическое руководство предназначено для студентов специальностей 110301,110302,110304.В настоящем указании разработаны задания к выполнению курсовой и расчетно-графических работ по динамике. Дана методика и примеры решения всех задач, а также теоретические вопросы и номера задач из сборника И.В. Мещерского, которые необходимо проработать для защиты работ. (по указанию преподавателя).
В каждой задаче дается 10 рисунков и таблица. Приступая к выполнению задания, студент должен выбрать номер рисунка по последней цифре шифра (номера зачетной книжки), а номер условия в таблице по последней. Например, если шифр оканчивается числом 25, то берутся: 5 рисунок и условие №2 из таблицы.
Задача Д-1
Интегрирование дифференциальных уравнений движения точки.
Условие:
Груз Д массой m получив в точке A начальную скорость 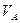 движется в изогнутой трубе АВС. На участке AB на груз действует постоянная сила
движется в изогнутой трубе АВС. На участке AB на груз действует постоянная сила 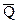 (её направление показано на рисунках). Трением груза о трубку на участке AB пренебречь.
(её направление показано на рисунках). Трением груза о трубку на участке AB пренебречь.
В точнее B груз, не изменял своей скорости, переходит на участок BC тубы, где на него кроме силы тяжести действует сила трения 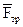 и переменная сила
и переменная сила 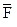 , проекция которой
, проекция которой 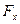 на ось Х задана в таблице.
на ось Х задана в таблице.
Считая груз материальной точкой и зная время t движения на участке AB, найти закон движения груза на участке BC, т.е. 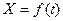 , где Х = ВД.
, где Х = ВД.
Решение задачи разбивается на две части. Сначала нужно составить дифференциальное уравнения движения точки (груза) на участке AB и проинтегрировать его методом разделения переменных, учитывая начальные условия. Затем, зная время движения груза на участке AB, определить скорость груза в точке B. Эта скорость будет начальной для движения груза в точке B. После этого нужно составить и проинтегрировать дифференциальное уравнение движения груза на участке BC также с учетом начальных условий. Получим скорость движения на участке BC. Учитывая, что 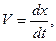 ещё раз проинтегрируем это уравнение методом разделения переменных. Полученный закон
ещё раз проинтегрируем это уравнение методом разделения переменных. Полученный закон 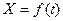 и будет являться законом движения груза на участке BC.
и будет являться законом движения груза на участке BC.
Таблица Д.1
| № условия | m, кг. | 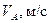 | Q, Н | t, с. | 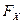 , Н , Н | 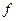  |
| 1.6 1.8 2.0 2.4 3.0 4.0 4.5 4.8 5.0 6.0 | 1.5 2.5 | 6sin(4t) -2cos(2t) 8t 8cos(4t) -3sin(2t) 4cos(2t) 4t -2cos(4t) -3sin(4t) 9t | 0.10 0.20 0.15 0.25 0.10 0.15 0.20 0.10 0.25 0.30 |
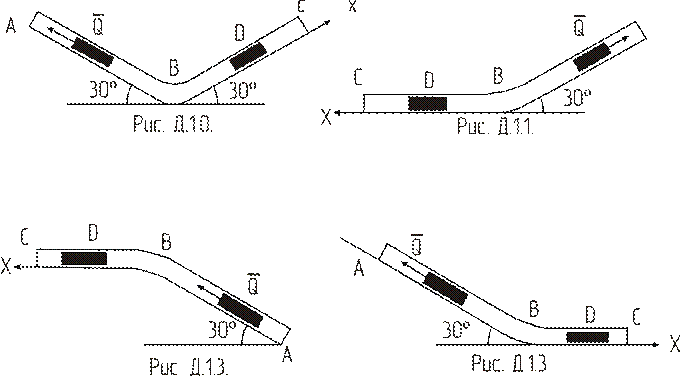

Пример Д.1.
На наклонном участке AB трубы (рис Д.1) на груз Д массой 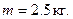 действует сила тяжести и постоянная сила Q=10 Н. В точке А груз имеет начальную скорость
действует сила тяжести и постоянная сила Q=10 Н. В точке А груз имеет начальную скорость 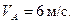 Движение от точки А до точки В длится
Движение от точки А до точки В длится 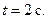 На горизонтальном участке BC Действует сила трения (коэффициент трения груза о трубу
На горизонтальном участке BC Действует сила трения (коэффициент трения груза о трубу 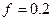 ) и переменная сила,
) и переменная сила, 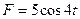 заданная в Ньютонах.
заданная в Ньютонах.
Определить: 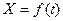 - закон движения груза на участке BC.
- закон движения груза на участке BC.
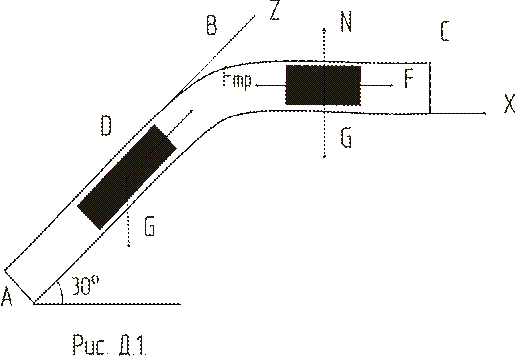
Решение:
- Рассмотрим движение груза на участке AB, считая груз материальной точкой. Изображаем положение груза в произвольный момент времени и все силы, действующие на него: силу тяжести
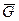 и силу
и силу 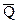 . Проводим ось AZ и составляем дифференциальное уравнение в проекции на эту ось:
. Проводим ось AZ и составляем дифференциальное уравнение в проекции на эту ось:
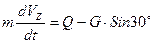 (1)
(1)
учитывая, что 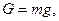 получим
получим
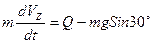 (2)
(2)
Разделяя обе части уравнения (2) на массу 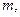 получим:
получим:
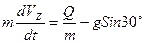
Затем разделим переменные (умножим обе части на 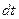 ) и проинтегрируем:
) и проинтегрируем:
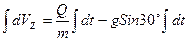
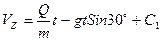 (3)
(3)
Для определения постоянной интегрирования 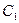 подставим в (3) начальные условия:
подставим в (3) начальные условия:
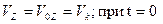
Получим 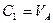
Тогда уравнение (3) имеет вид:
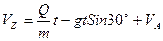 (4)
(4)
Подставив в (4) данные условия задачи, определим скорость груза в точке B:
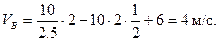
- Рассмотрим движение груза на участке BC. Найденная скорость
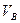 будет для движения на этом участке начальной. Изображаем груз в произвольном положении и действующие на него силы: силу тяжести
будет для движения на этом участке начальной. Изображаем груз в произвольном положении и действующие на него силы: силу тяжести 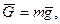 силу трения
силу трения 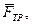 нормальную реакцию
нормальную реакцию 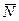 и силу
и силу 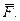
Запишем дифференциальное уравнение движения груза в проекции на ось BX:
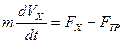 (5)
(5)
где 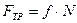
Для определения 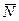 составим уравнение в проекции на ось By:
составим уравнение в проекции на ось By:
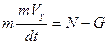 (6)
(6)
Так как движение груза вдоль оси y отсутствует, то, 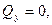 следовательно (6) примет вид:
следовательно (6) примет вид:
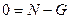
Откуда 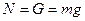
Тогда сила трения 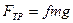
С учетом этого (5) примет вид:
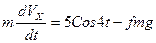 (7)
(7)
Разделив обе части на m и подставив в (7) данные условия задачи, получим:
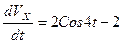 (8)
(8)
Умножая обе части уравнения (8) на 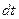 и интегрируя, находим:
и интегрируя, находим:
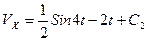 (9)
(9)
Подставив в (9) начальные условия 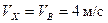 и
и 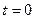 получим:
получим: 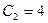
При найденном значении 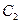 уравнение (9) даст:
уравнение (9) даст:
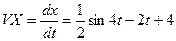 (10)
(10)
Умножая обе части (10) на 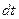 и снова интегрируя, найдем:
и снова интегрируя, найдем:
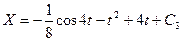 (11)
(11)
Так как при 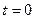 и
и 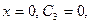 то получим искомый закон движения груза:
то получим искомый закон движения груза:
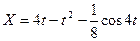
Вопросы к защите задачи Д.1.
1. Основные законы динамики.
2. Дифференциальные уравнения движения материальной точки в декартовых координатах.
3. Естественные уравнения движения материальной точки.
4. Первая задача динамики, её сущность и методы решения.
5. Вторая задача динамики, её сущность и методы решения.
6. Постоянные интегрирования и их определение по начальным условиям.
7. Интегрирование диф. уравнений движения точки, когда сила зависит от координат.
8. Интегрирование диф. уравнений движения точки, когда они зависят от времени.
9. Интегрирование диф. уравнений движения точки, когда они зависят от скорости.
10. Дифференциальные уравнения свободных колебаний.
Задача Д-2
Применение теорем динамики к исследованию движения материальной точки.
Условие:
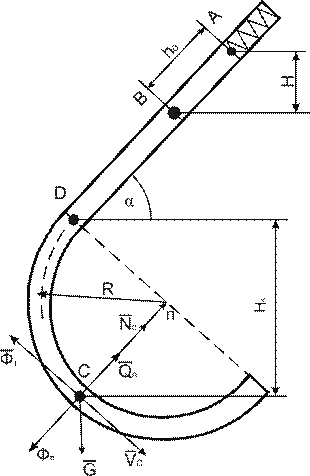
Шарик массой m, принимаемый за материальную точку, движется из положения A внутри трубы со скоростью 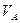 . Пройдя путь
. Пройдя путь 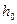 , шарик отделяется от пружины, коэффициент тяжести которой С.
, шарик отделяется от пружины, коэффициент тяжести которой С.
Определить скорость шарика в положениях B,C,Д и давление шарика на стенку трубки в положении С. Трением шарика на криволинейных участках траектории можно пренебречь.
Для определения скорости точки используем теорему об изменении кинетической энергии материальной точки:
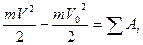 (1)
(1)
В случае, когда задано время прохождения участка, применяется теорема об изменении количества движения материальной точки:
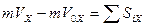 (2)
(2)
где 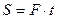 - импульс силы.
- импульс силы.
Для определения давления шарика на стенку канала используем принцип Даламбера для материальной точки, на основании которого геометрическая сумма сил, приложенных к точке, и силы инерции этой точке равны нулю:
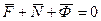 (3)
(3)
Сила инерции величина фиктивная и мы прикладываем её условно.
В случае движения по окружности 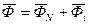 , где,
, где, 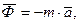 т.е. направлена в сторону противоположную ускорению.
т.е. направлена в сторону противоположную ускорению.
При решении задачи необходимо учесть, что работы силы упругости определяется по формуле:
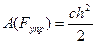
и будет положительная, если деформация пружины уменьшается.
Работа силы трения:
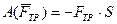
и будет отрицательной, так сила трения направлена в сторону, противоположную движению.
Работа силы тяжести:
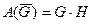
и будет положительной, если тело приближается к земле. В формуле работы H – величина вертикального перемещения точки.
Таблица Д.2.
| № условия | m кг | 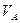 м/с м/с | 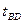 c. c. | R м | 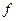 | 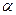 град град | 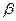 град град | h см | с Н/см |
| 0,5 0,6 0,8 0,6 0,7 0,2 0,4 0,1 0,3 0,5 | 0,2 0,3 0,5 0,2 1,0 0,1 0,4 0,5 | 0,2 1,5 0,5 0,4 0,6 | 0,2 0,1 0,1 0,2 0,2 0,1 0,3 0,1 0,1 0,2 | 1,2 1,1 0,8 0,4 |
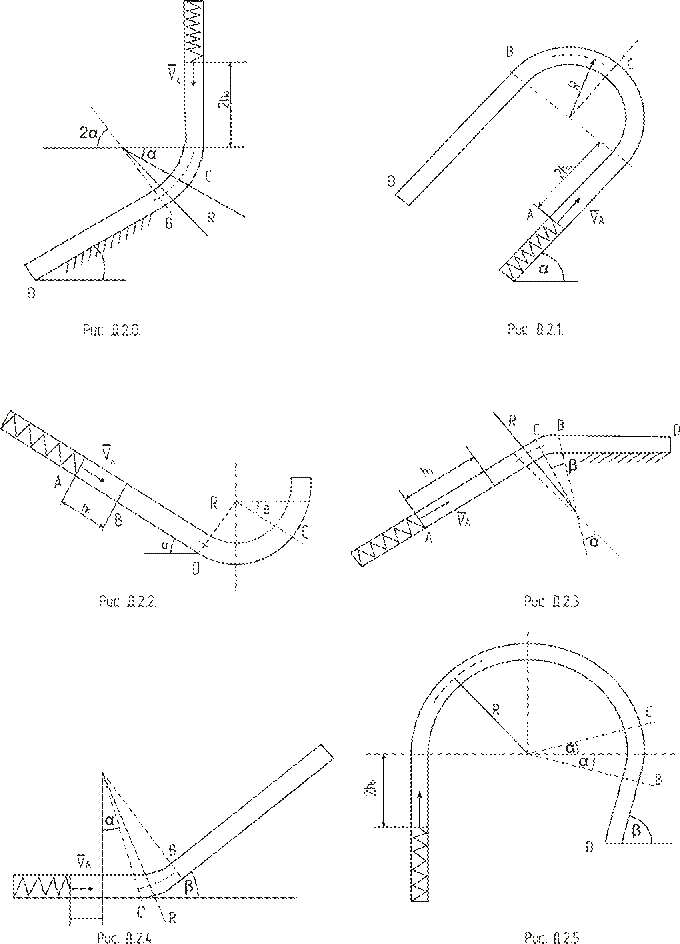

Пример Д-2.
Шарик массой 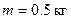 движется из положения А внутри трубы, со скоростью
движется из положения А внутри трубы, со скоростью 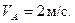 Пройдя путь
Пройдя путь 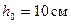 шарик определяется от пружины коэффициент жесткости которой
шарик определяется от пружины коэффициент жесткости которой 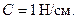 (100 Н/м). Коэффициент трения на прямолинейном участке
(100 Н/м). Коэффициент трения на прямолинейном участке 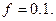 Радиус кривизны траектории
Радиус кривизны траектории 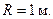 Время прохождения участка ВД
Время прохождения участка ВД 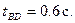 Угол наклона трубы
Угол наклона трубы 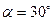
Определить: 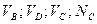 .
.
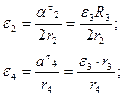
Определяем моменты инерции:
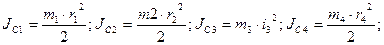
Выражаем все главные векторы и главные моменты сил инерции:
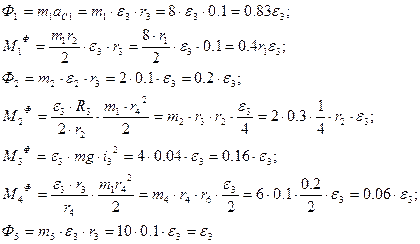
 Так как на основании принципа Даламбера система уравновешена, то мы сможем применить к ней принцип возможных перемещений.
Так как на основании принципа Даламбера система уравновешена, то мы сможем применить к ней принцип возможных перемещений.
- Даем системе возможное перемещение. Повернем тело 3. на угол
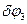 вокруг оси
вокруг оси 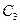 . Тогда тела входящие в систему получат соответственно возможное перемещение.
. Тогда тела входящие в систему получат соответственно возможное перемещение.
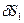 - Перемещение т.
- Перемещение т. 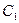 .
.
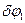 - Поворот тела 1.
- Поворот тела 1.
Тело 2.: 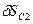 - Перемещение т.
- Перемещение т. 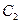 .
.
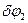 - Угол поворота тела 2.
- Угол поворота тела 2.
Тело 4.: 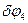 - Угол поворота тела 4.
- Угол поворота тела 4.
Тело 5.: 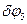 - Перемещение тела 5.
- Перемещение тела 5.
- Выражаем все возможные перемещения через
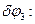
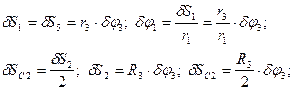
 Решение.
Решение.
Для определения скорости шарика в положении В применим теорему об изменении кинетической энергии материальной точки (1).
Движение шарика на участке AВ траектории происходит под действием силы упругости 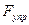 силы трения скольжения
силы трения скольжения 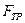 и силы тяжести G (Рис. Д.2.1)
и силы тяжести G (Рис. Д.2.1)
За начальную скорость принимаем скорость шарика в положении A,
тогда:
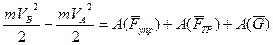 (4)
(4)
Подставив в (4) значение работ, получим:
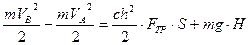
Учитывая, что 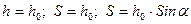
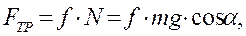 получим:
получим:
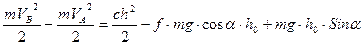 (5)
(5)
Разделим (5) на массу и домножив на 2:
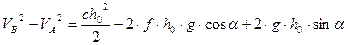
Отсюда:
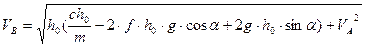 (6)
(6)
Подставив в (6) данные условий задачи, получим:
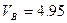 м/с
м/с
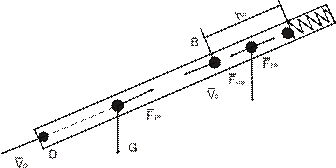 Для определения скорости шарика в положении Д применим теорему об изменении количества движения материальной точки (2). Движение шарика на участке ВД траектории происходит под действием силы трения и скольжения
Для определения скорости шарика в положении Д применим теорему об изменении количества движения материальной точки (2). Движение шарика на участке ВД траектории происходит под действием силы трения и скольжения 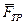 и силы тяжести
и силы тяжести 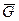 (Рис. Д.2.1).За начальную скорость шарика принимаем скорость в положении В. тогда:
(Рис. Д.2.1).За начальную скорость шарика принимаем скорость в положении В. тогда: 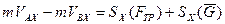 (7)
(7)
где: 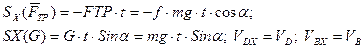
Тогда (7) примет вид: 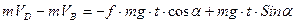
Разделим (8) на массу: 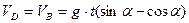
подставив данные условия задачи, получим: 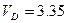 м/с.
м/с.
Для определения скорости шарика в положении С применим теорему об изменении кинетической энергии материальной точки. Движение шарика на участке ДС траектории происходит только под действием силы тяжести 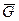 . Скорость шарика в положении Д принимаем за начальную тогда:
. Скорость шарика в положении Д принимаем за начальную тогда:

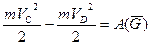 (9)
(9)
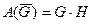 ; где
; где 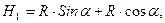
тогда (9) примет вид: 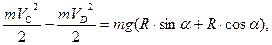
Разделим это выражение на массу и домножим на 2:
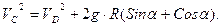 (10)
(10)
Подставив в (10) данные условия задачи получим:
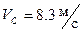
Для определения давления шарика на стенку канала в положении С применим принцип Даламбера для материальной точки (3).
Добавим к действующим на точку силам 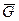 и
и 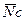 силу инерции
силу инерции 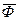 . Тогда в проекции на нормаль сумма всех сил должна быть равна 0.
. Тогда в проекции на нормаль сумма всех сил должна быть равна 0.
и 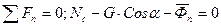
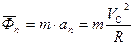 ,
,
Тогда 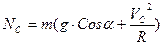 (11)
(11)
Подставив в (11) все значения, получим: 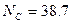 Н.
Н.
Вопросы к защите задачи Д - 2.
- Теорема об изменении кинетической анергии материальной точки.
- Понятие о работе и мощности, единицы измерения.
- Работа силы тяжести.
- Работа упругой силы.
- Теорема об изменении количества движения материальной точки.
- Импульс силы. Единицы измерения.
- Теорема об изменении момента количества движения материальной точки.
- Принцип Даламбера для материальной точки.
- Сила инерции материальной точки.
- Понятие о количестве движения.
Задача Д-3
Условие:
Механическая система состоит из грузов 1 и 2 ступенчатого шкива 3 с радиусом ступеней 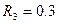 м
м 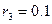 м. и радиусом инерции
м. и радиусом инерции 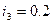 м. блока 4 радиуса
м. блока 4 радиуса 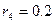 м. и катка (или неподвижного блока) 5: тело 5 считать сплошным однородным цилиндром, а массу блока 4 равномерно распределенной по ободу. Коэффициент трения грузов о плоскость
м. и катка (или неподвижного блока) 5: тело 5 считать сплошным однородным цилиндром, а массу блока 4 равномерно распределенной по ободу. Коэффициент трения грузов о плоскость 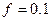 .
.
Тела системы соединены нерастяжными нитями, участки которых параллельны соответствующим плоскостям. К одному из тел приложена пружина с коэффициентов жесткости с. Под действием силы 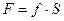 система приходит в движение из состояния покоя деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сия сопротивления. Все катки катятся без скольжения .Определить значение искомой величины указанной в таблице, когда перемещение
система приходит в движение из состояния покоя деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сия сопротивления. Все катки катятся без скольжения .Определить значение искомой величины указанной в таблице, когда перемещение 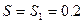 м.
м.
Задача решается тремя методами:
При помощи теоремы об изменении кинетической энергии системы: 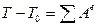
При помощи общего уравнения динамики: 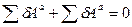
При помощи уравнения Лагранжа II рода: 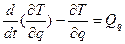
Таблица Д.З
| № Усл. | 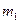 Кг Кг | 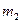 Кг Кг | 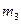 Кг Кг | 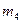 Кг Кг | 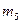 Кг Кг | 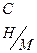 | M | 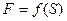 H H | Найти |
| 1,2 0.8 1.4 1.8 1.2 1.8 0.8 1.4 1.4 1.6 | 50(4+5S) 50(8+3S) 60(6+5S) 50(5+6S) 40(9+4S) 50(7+8S) 40(8+9S) 60(8+5S) 50(9+2S) 80(6+7S) | 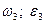 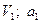 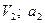 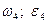 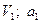 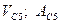 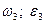 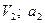 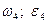 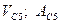 |

Пример Д-3.
Дано: 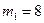 кг,
кг, 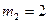 кг,
кг, 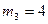 кг,
кг, 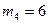 кг,
кг, 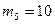 10кг,
10кг, 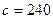 Н/м,
Н/м, 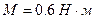 ,
, 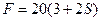 H.
H.
Определить: угловую скорость 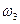 и угловое ускорение
и угловое ускорение 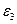 шкива 3 в тот момент, когда система переместится на величину S.
шкива 3 в тот момент, когда система переместится на величину S.
1 метод.
Для определения угловой скорости 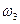 шкива 3 применяем теорему об изменении кинетической энергии системы.
шкива 3 применяем теорему об изменении кинетической энергии системы.
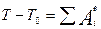
 Решение:
Решение:
Рассмотрим движение системы. Изобразим все действующие на неё внешние силы: 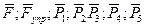 , реакции
, реакции 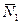 и
и 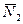 , силу трения
, силу трения 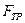 и момент М.
и момент М.
I) Определяем кинетическую энергию системы. Так как в начальный момент система находилась в покос, то 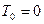 . Величина T равна сумме кинетических энергий всех тел системы:
. Величина T равна сумме кинетических энергий всех тел системы:
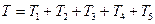 (2)
(2)
Кинетическая энергия тела определяется в зависимости от вида движения. Тело 1 совершает плоскопараллельное движение: Его кинетическая энергия: 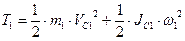
Выражаем все скорости через искомую 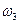 :
:
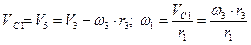
учитывая, что 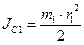 кинетическая энергия тела 1 будет:
кинетическая энергия тела 1 будет:
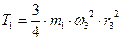 (3)
(3)
Тело 2 совершает плоскопараллельное движение: 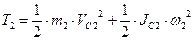
Выражаем 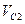 и
и 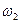 через
через 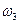 :
:
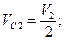
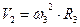 , тогда
, тогда 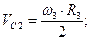
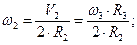
учитывая что 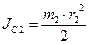 , кинетическая энергия тела 2 будет:
, кинетическая энергия тела 2 будет:
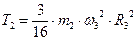 (4)
(4)
Тело 3 вращается вокруг неподвижной оси. Его кинетическая:
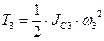
Учитывая, что 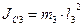 , кинетическая энергия тела 3 будет:
, кинетическая энергия тела 3 будет:
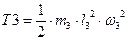 (5)
(5)
Тело 4 вращается, поэтому:
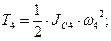
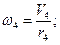
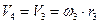 , тогда
, тогда 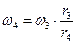
учитывая, что 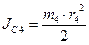 , кинетическая энергия тела 4 будет:
, кинетическая энергия тела 4 будет:
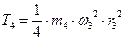 (6)
(6)
Тело 5 движется поступательно. Его кинетическая энергия:
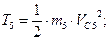
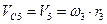
Тогда: 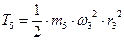 (7)
(7)
Подставив (3) (4) (5) (6) (7) в выражение (2),получим
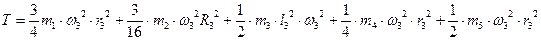
Подставив в это уравнение данные условия задачи, получим:
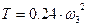 (8)
(8)
Примечания: если масса какого-то тела равна нулю, то и его кинетическая энергия равна 0.
Определяем сумму работ всех действующих на систему внешних сил, в зависимости от заданного перемещения.
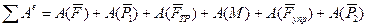 (9)
(9)
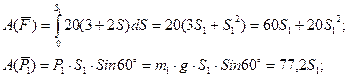
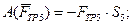 учитывая, что
учитывая, что 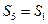

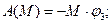
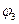 - угол поворота шкива 3.
- угол поворота шкива 3.
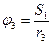 , тогда:
, тогда:
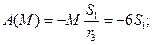
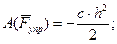 h - Удлинение пружины.
h - Удлинение пружины.
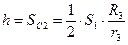
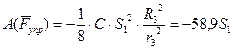
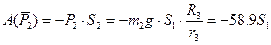
Подставив значение всех работ в (9), получим:
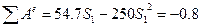 Н.м. (10)
Н.м. (10)
Приравняв (8) и (10) на основании (1), получим:
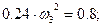
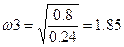
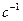
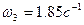
II) Способ. С помощью общего уравнения динамики определяем угловое ускорение 3 тела 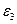 .
.
Общее уравнение динамики объединяет два принципа; Даламбера и возможных перемещений.
Принцип Даламбера: Если ко всем действующим на систему силам добавить главный вектор и главный момент сил инерции, то система будет находиться в состоянии равновесия.
Принцип возможных перемещений: случае равновесия и идеальных связей сумма элементарных работ всех активных сил при всяком возможном перемещении равна нулю.
Поэтому общее уравнение примет вид:
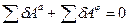 (11)
(11)
где: 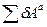 - сумма элементарных работ всех активных сил.
- сумма элементарных работ всех активных сил.
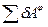 - сумма элементарных работ всех сил инерции.
- сумма элементарных работ всех сил инерции.
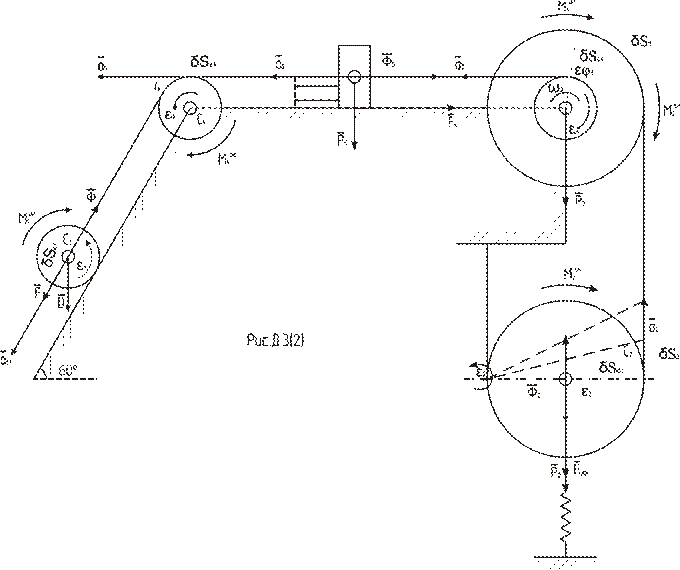
Этим способом задача решается в следующей последовательности:
I Принимаем принцип Даламбера для механической системы, для чего ко всем действующим на данную систему силам добавим главные векторы и главные моменты сил инерции.
Тело 1 совершает плоско-параллельное движение, состоящее из поступательного движения центра катка С1 (и вращательного вокруг этого центра. Поэтому добавляем к действующим на него силам 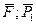 и
и 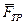 главный вектор,
главный вектор, 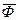 и главный момент
и главный момент 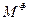 сил инерции.
сил инерции.
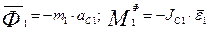
Тело 2 совершает плоско-параллельное движение. Поэтому добавляем
к действующим на него силам 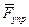 и
и 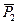 главный вектор,
главный вектор, 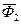 и главный момент сил инерции
и главный момент сил инерции 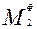
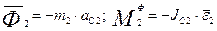
Тело З совершает вращательное движение. Поэтому прикладываем к нему главный момент сил инерции 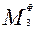
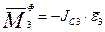
Тело 4 совершает вращательное движение. Поэтому прикладываем к нему главный момент сил инерции 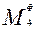 .
.
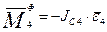
Тело 5 движется поступательно. Поэтому к действующим на него силам 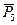 и
и 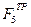 - главный вектор сил инерции
- главный вектор сил инерции 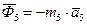
Примечание: Если масса какого-то тела, равна нулю, то главный вектор и главный момент сил инерции к нему не прикладывается.
2)Выражаем все ускорения через угловое ускорение тела 3:
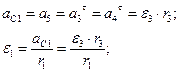
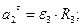
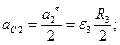
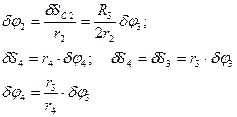 с
с
III. Определяем сумму элементарных работ:
Всех активных сил:
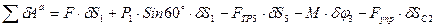
подставив значение всех возможных перемещений в зависимости от 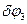 получим:
получим:
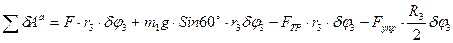 (12)
(12)
2)Всех сил инерции:
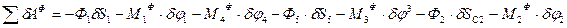
Подставив значения всех перемещений в зависимости от 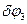 получим:
получим:
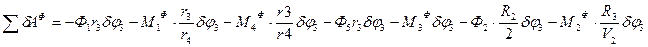
(13)
Подставляя выражение (12) и (13) в (11) получим:
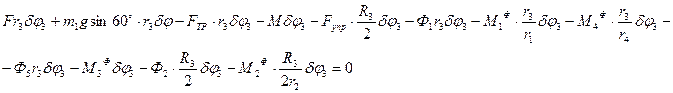
Разделим выражение на 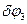
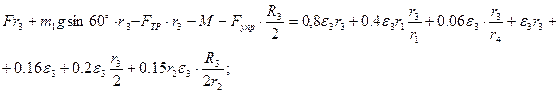
и подставим в него значение всех сил и моментов, учитывая, что:
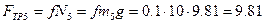 Н
Н
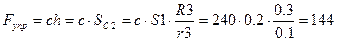 Н
Н
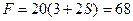 Н
Н
Получим:
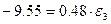
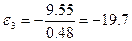
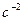
3 Способ. С помощью уравнения Лагранжа II рода определяем угловое ускорение третьего тела 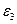 .
.
- Этим методом задача решается в следующей последовательности: Определяем число обобщенных координат, которое равно числу степеней свободы. Обобщенная координата - это независимая величина, которая определяет положение всей системы .Данная система имеет одну степень свободы, следовательно, и одну обобщенную координату.
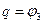
- Записываем уравнение Лагранжа II рода:
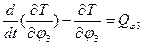 (14)
(14)
где: Т - кинетическая энергия системы,
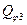 - обобщенная сила по данной обобщенной координате.
- обобщенная сила по данной обобщенной координате.
- Определяем кинетическую энергию системы. Из 1 метода на основании (8):
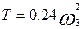
Так как 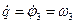 , то кинетическую энергию можно записать в функции от обобщенной скорости:
, то кинетическую энергию можно записать в функции от обобщенной скорости:
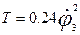
- Определяем частную производную от кинетической энергии по
обобщенной скорости:
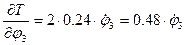
- Определяем производную по времени:
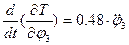 (15)
(15)
- Так как кинетическая энергия не зависит от обобщенной координаты, то
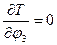 .
. - Определяем обобщенную силу:
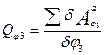
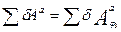 - сумма элементарных работ всех активных пил сил определяется при решении задачи II методом.
- сумма элементарных работ всех активных пил сил определяется при решении задачи II методом.
Выражение (12)
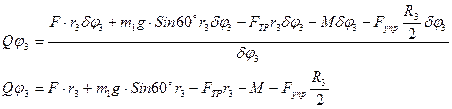
8 Значение найденных величин (15) и (16) подставим в (14)
Вопросы к защите задачи Д - 3
- Понятие о кинетической энергии. Кинетическая энергия механической системы.
- Формулы по определенно кинетической энергии твердого тела:
- при поступательном движении.
- при вращательном движения.
- при плоскопараллельном движении.
- Теорема об изменении кинетической анергии механической системы.
- Понятие о работе, единицы измерения работы.
- Понятие об элементарной работе, формула по её определению.
- Работа силы тяжести.
- Работа силы упругости.
- Работ,а силы трения.
- Работа силы, приложенной к вращающемуся телу.
- Главный вектор и главный момент сил инерции, формулы по их определению.
- Принцип Даламбера для механической системы, его сущность.
- Понятие об возможном перемещении.
- Принцип возможных перемещений, его сущность.
- Общее уравнение динамики, его сущность.
- Понятие об обобщенной координате, определение числа обобщенных координат для данной механической системы.
- Понятие об обобщенной скорости, единицы измерения.
- Понятие об обобщенной силе, единицы измерения.
- Уравнение Лагранжа II рода.
Тест К-1.
I В каком случае движение точки задано векторным способом?

1) 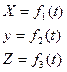
II В период разгона маховик вращается вокруг своей оси по закону 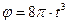 Определить угловую скорость и угловое ускорение маховика в тот момент, когда он сделает 4 оборота.
Определить угловую скорость и угловое ускорение маховика в тот момент, когда он сделает 4 оборота.
1) 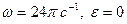 2)
2) 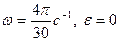
3) 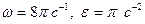 4)
4) 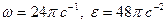
III 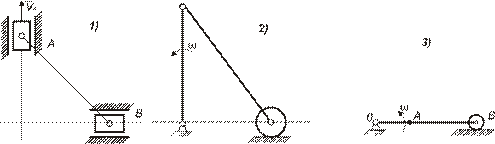 В каком случае скорость точки B ровна нулю?
В каком случае скорость точки B ровна нулю?
IV Какая из четырех точек – точка C.

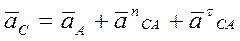
V 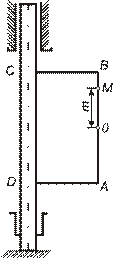 Рамка вращается вокруг оси CD по закону
Рамка вращается вокруг оси CD по закону 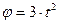 . Вдоль рамки движется точка M по закону
. Вдоль рамки движется точка M по закону 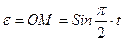 . Как определяется ускорение точки M в относительном движении?
. Как определяется ускорение точки M в относительном движении?
1) 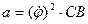
2) 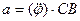
3) 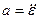
Тест К-2.
I По какой формуле определяется касательное ускорение точки?
1) 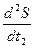 2)
2) 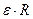 3)
3) 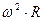
II Колесо, радиусом 80 см. вращается в период разгона равноускоренно из состояния покоя, совершило за некоторое время 750 оборотов. Определить время разгона, если скорости точек на ободе достигали при этом 200 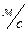 .
.
1) 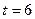 с. 2)
с. 2) 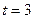 с. 3)
с. 3) 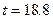 с. 4)
с. 4) 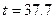 с.
с.
III 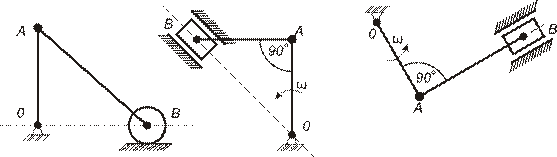 В каком из представленных случаев
В каком из представленных случаев 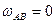 ?
?
IV Для определения ускорения, какой точки механизма записано уравнение и показаны вектора.
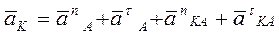

V 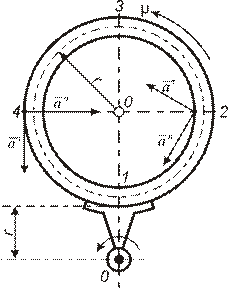 Кольцо вращается ускоренно относительно оси, проходящей через точку 0. По кольцу ускоренно движется точка M. Во втором или четвертом положении точки M показаны векторы, составляющие ускорение точки M в переносом движении.
Кольцо вращается ускоренно относительно оси, проходящей через точку 0. По кольцу ускоренно движется точка M. Во втором или четвертом положении точки M показаны векторы, составляющие ускорение точки M в переносом движении.
Тест К-3.
I 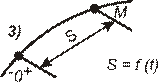 В каком случае движение точки задано естественным способом?
В каком случае движение точки задано естественным способом?
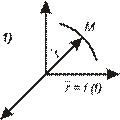 2)
2) 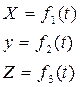
II По какой формуле определяется нормальное ускорение точки?
1) 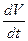 2)
2) 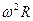 3)
3) 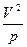 4)
4) 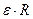 5)
5) 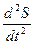
III Вращение тело вокруг неподвижной оси задано уравнением 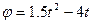 . Определить скорость и ускорение точки тела, отстоящей от оси вращения на 0,2 м. в момент
. Определить скорость и ускорение точки тела, отстоящей от оси вращения на 0,2 м. в момент 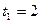 ?
?
1) 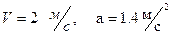 2)
2) 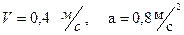
3) 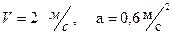 4)
4) 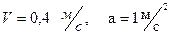
IV В каком из перечисленный случаев, мгновенный центр скоростей лежит в точке D?
V 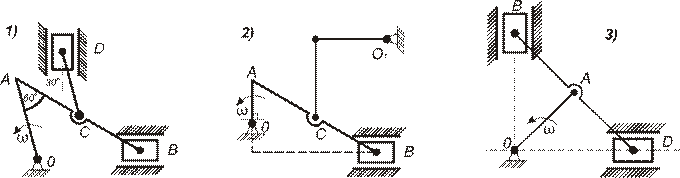 Наклонная плоскость AB движется прямолинейно со скоростью 0,1 м./с. По этой плоскости спускается тело со скоростью 0,2 м/с. Какова переносная скорость движения тела P.
Наклонная плоскость AB движется прямолинейно со скоростью 0,1 м./с. По этой плоскости спускается тело со скоростью 0,2 м/с. Какова переносная скорость движения тела P.
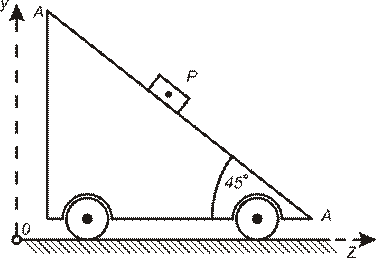
1) 0,1 М/с.
2) 0,2 М/c.
3) 0.3 M/c
Тест К-4.
I Какое уравнение траектории имеет точка при данном законе её движения?
1) 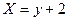 2)
2) 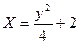 3)
3) 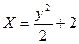
II Маховик, радиусом 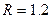 м. вращается равномерно, делая
м. вращается равномерно, делая 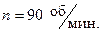 Определить скорость и ускорение точки, лежащей на ободе маховика.
Определить скорость и ускорение точки, лежащей на ободе маховика.
1) 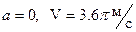 2)
2) 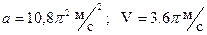 3)
3) 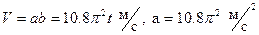
III В каком случае мгновенный центр скоростей лежит в точке B?
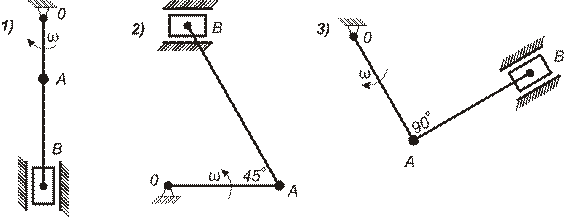
IV Определить угловое ускорение диска радиусом 1 м., катящегося без скольжения по наклонной поверхности, если скорость Т.М 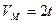

1) 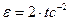
2) 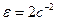
3) 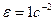
V В каком из указанных случаев движения кориолисово ускорение равно нулю?
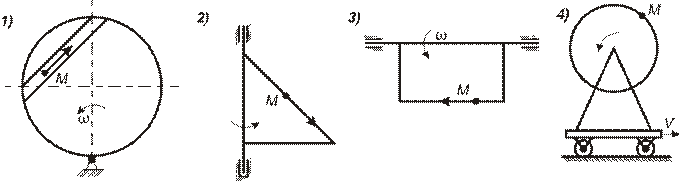
Тест К-5
I Какое уравнение траектории имеет точка при данном законе её движения? 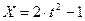 ;
; 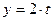
1) 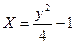 2)
2) 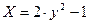 3)
3) 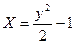
II Вращение тела вокруг неподвижной оси задано уравнением 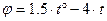 рад. Определить скорость и ускорение точки тела, отстоящей от оси вращения на 0,2 м. в момент
рад. Определить скорость и ускорение точки тела, отстоящей от оси вращения на 0,2 м. в момент 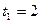 с.
с.
1) 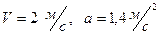 2)
2) 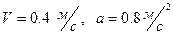
3) 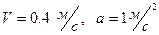 4)
4) 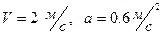
III 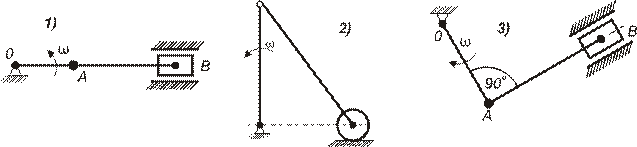 В каком случае
В каком случае 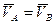 ?
?
IV Определить угловое ускорения диска радиусом 0,5 м. катящегося без скольжения прямолинейно по горизонтальной поверхности. В данный момент времени: 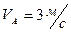 ,
, 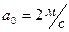
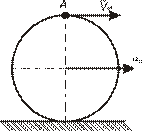
1) 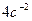
2) 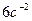
3)