Следствия автокорреляции остатков

Понятие автокорреляции

Определение: Автокорреляция — это взаимосвязь последовательных элементов временного или пространственного ряда данных.

В эконометрических исследованиях часто возникают и такие ситуации, когда дисперсия остатков постоянная, но наблюдается их ковариация. Это явление называютавтокорреляцией остатков.

Автокорреляция остатков чаще всего наблюдается тогда, когда эконометрическая модель строится на основе временных рядов. Если существует корреляция между последовательными значениями некоторой независимой переменной, то будет наблюдаться и корреляция последовательных значений остатков.

Автокорреляцияможет быть также следствием ошибочной спецификации эконометрической модели. Кроме того, наличие автокорреляции остатков может означать, что необходимо ввести в модель новую независимую переменную.

Проиллюстрируем проблему автокорреляции остатков на примере эконометрической модели с двумя переменными. Пусть

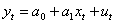(1)

где мы предполагаем, что остатки u_t, удовлетворяют схему авторегресии первого порядка, то есть зависят только от остатков предыдущего периода:

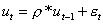(2)

для которой |ρ| < 1, а ε_t имеют такие свойства:

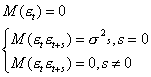
Величина ρ характеризует уровень взаимосвязи каждого следующего значения с предыдущим то есть ковариацию остатков.

Спецификация модели (1) имеет индекс t, что свидетельствует о ее динамическом характере, то есть и — период времени, для которого строится такая модель динамических (временных) рядов исходных данных.

Рассмотрим остатки модели u_t, учитывая (2):

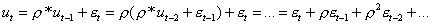
Отсюда

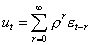. (3)

Поскольку: 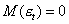, то .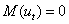

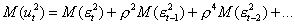
Учитывая, что последовательные значения 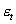, независимы, запишем

.

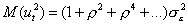Тогда

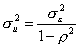. (4)

Ковариация последовательных значений остатков запишется в виде

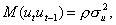
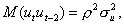
и в общем случае

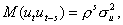(5)

то есть для модели (1) не удовлетворяется гипотеза о независимости последовательных значений остатков.

Выражение (5) можно записать так:

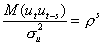. (6)

Это означает, что при наличии автокорреляции остатков второе необходимое условие подается в виде:

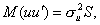
где S - матрица коэффициентов автокорреляции s-го порядка для ряда u_t,, или

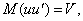
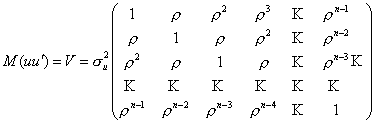. (7)

Сравнив матрицу, которую имеем в данном случае, с матрицей при наличии гетероскедастичности, увидим, что они существенным образом отличаются одна от другой. Это связано с тем, как понимается второе условие для применения метода МНК при явлении гетероскедастичности и автокорреляции.

Итак, для гетероскедастичных остатков существует одна форма нарушения стандартной гипотезы, в соответствии с которой М(ии')=σ²_u*S, для автокореляционных остатков мы сталкиваемся с второй формой нарушения этой гипотезы.

Следствия автокорреляции остатков

Если пренебречь автокорреляцией остатков и оценить параметры модели МНК, то придем к такимтрем следствиям.

1. Оценки параметров модели могут быть несмещенными, но неэффективными, то есть выборочные дисперсии вектора оценок А могут быть неоправданно большими.

2. Поскольку выборочные дисперсии исчисляются не по уточненным формулам, то статистические критерии t- и F-статистики, которые найдены для линейной модели, практически не могут быть использованы в дисперсионном анализе.

3. Неэффективность оценок параметров эконометрической модели приводит, как правило, к неэффективным прогнозам, то есть прогнозам с очень большой выборочной дисперсией.

Коэффициент детерминации, как и коэффициент корреляции, принимает значения от -1 до +1. Чем ближе его значение коэффициента по модулю к 1, тем теснее связь результативного признака Y с исследуемыми факторами X.

Например, если получают коэффициент детерминации R2 = 0,9, значит уравнением регрессии объясняется 90% дисперсии результативного признака, а на долю прочих факторов приходится 10% ее дисперсии (т.е. остаточная дисперсия). Величина коэффициента детерминации служит важным критерием оценки качества линейных и нелинейных моделей. Чем значительнее доля объясненной вариации, тем меньше роль прочих факторов, и значит, модель регрессии хорошо аппроксимирует исходные данные и такой регрессионной моделью можно воспользоваться для прогноза значений результативного показателя.

Частная корреляция

Ранжирование факторов в множественной линейной регрессии, может быть проведено через стандартизованные коэффициенты регрессии. Эту цель можно достигнуть с помощью частных коэффициентов корреляции для линейных связей. При нелинейной связи исследуемых признаков эту функцию выполняют частные индексы детерминации. Помимо этого, частные коэффициенты корреляции широко используют при решении проблемы отбора факторов: целесообразность включения фактора в модель может определяться величиной частных коэффициентов корреляции.

Частные коэффициенты корреляции характеризуют тесноту связи между результатом и фактором при устранении влияния другого фактора (или факторов), которые включенны в уравнение регрессии.

Показатели частной корреляции определяются как отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в регрессионную модель.

Частные коэффициенты корреляции, рассчитанные по рекуррентной формуле могут находиться в пределах от -1 до +1, а по формулам через множественные коэффициенты детерминации — от 0 до 1. Сравнивая их друг с другом можно ранжировать факторы по тесноте их связи с результатом.

Частные коэффициенты на основе стандартизованных коэффициентов регрессии (бета-коэффициентов) дают меру тесноты связи каждого фактора с показателем (результатом) в чистом виде. Если из стандартизованного уравнения регрессии следует, что бета 1 > бета 2 > бета 3, т.е. по силе влияния факторов на результат их порядок таков: х1, х2, х3, такой же порядок факторов определяется и по соотношению частных коэффициентов корреляции.

Т.е. в двухфакторном анализе частные коэффициенты корреляции — это стандартизованные коэффициенты регрессии, которые умноженны на квадратный корень из соотношения долей остаточных дисперсий фиксируемого фактора на фактор и на результат. В эконометрике коэффициенты частной корреляции в основном не имеют самостоятельного значения. Их, как правило, используют на стадии формирования модели, зачастую в процедуре отсева факторов.

Мультиколлинеарность

Коэффициенты интеркорреляции (т. е. сила связи между объясняющими переменными) позволяют исключить из модели регрессии дублирующие факторы. Две переменных явно коллинеарны, когда они находятся между собой в линейной зависимости, если коэффициент корреляции > 0,7.

Поскольку одним из условий нахождения уравнения множественной регрессии является независимость действия факторов, коллинеарность факторов нарушает это условие. Если факторы модели коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии.

Предпочтение в эконометрике отдается не фактору, более сильно связанному с результатом, а фактору, который при сильной связи с результатом имеет наименьшую тесноту связи с другими факторами. Т.е. коэффициент корреляции между факторами меньше 0,3 или, в идеале, близок к нулю. В этом условии проявляется специфика множественной регрессии как метода исследования комплексного влияния факторов на результат в условиях их независимости друг от друга.