Оптимальное смешивание (составление рациона питания, смесей, задача о диете и т.д.).

Пусть дневной рацион должен содержать m видов различных питательных веществ соответственно в количестве не менее b_i (i=1,2,...,m) единиц. Имеется n видов различных продуктов в количестве d_j (j=1,2,…,n) единиц.

Пусть a_ij (i=1,2,...,m; j=1,2,...n) - количество единиц i-го питательного вещества, содержащегося в единице j-го продукта;

C_j – стоимость (вес, калорийность и т.д.) единицы j-го продукта;

x_j (j=1,2,…,n) - количество единиц j-го продукта в дневном рационе.

Определить, какие продукты и в каком количестве необходимо включить в рацион, чтобы он удовлетворял минимальной дневной потребности в каждом питательном веществе при наименьшей общей стоимости используемых продуктов, т.е. найти минимальное значение линейной функции L=C₁x₁+C₂x₂+××××+C_nx_n при ограничениях

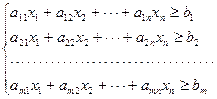
x_j ³ 0, (j=1,2,×××,n), b_i ³ 0 (i=1,2, ××× ,m).

К этому же классу задач относится задача оптимального использования материалов при условии, что заданный план изготовления деталей может быть выполнен или перевыполнен.

Для производства m видов деталей соответственно в количестве не менее b_i (i=1,2,...,m) единиц используется n видов материалов, имеющихся в количестве d_j (j=1,2,…,n) единиц.

Пусть a_ij (i=1,2,...,m; j=1,2,...n) - количество деталей i-го вида, которые можно изготовить из единицы j-го материала;

C_j – стоимость единицы j-го материала;

Определить, какие материалы и в каком количестве надо использовать, чтобы изготовить деталей не меньше, чем запланировано, при минимальной суммарной стоимости материалов. Пусть x_j (j=1,2,…,n) – расход материала j-го вида, тогда математическая модель: найти минимальное значение линейной функции L= 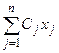при ограничениях: 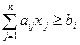, i=1,2,…,m, 0£x_j£d_j , j=1,2,…,n.

Пример 2. Для составления рациона используют два вида корма I и II, содержащие питательные вещества (витамины) S₁, S₂ и S₃. При откорме каждое животное ежедневно должно получить не менее 9 ед. питательного вещества S₁, не менее 8 ед. вещества S₂ и не менее 12 ед. вещества S₃. Содержание количества единиц питательных веществ в 1 кг каждого вида корма и стоимость 1 кг корма приведены в табл. 3.

Таблица 3.

Питательные вещества	Минимальная норма	Количество единиц питательных веществ в 1 кг корма
		корм 1	корм 2
S1
S2
S3
Стоимость 1 кг. корма (в коп.)

Необходимо составить дневной рацион нужной питательности, причем затраты на него должны быть минимальными.

Решение. Составим экономико-математическую модель задачи.

Обозначим через x₁ и x₂ соответственно количество килограммов корма I и корма II в дневном рационе. Принимая во внимание значения, приведенные в табл.3, и условие, что дневной рацион удовлетворяет требуемой питательности только в случае, если количество единиц питательных веществ не меньше предусмотренного, получаем систему ограничений:

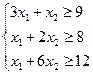(6)

x₁³0, x₂³0 (7)

Если корм I не используется в рационе, то x₁=0; в противном случае x₁>0. Аналогично имеем x₂³0, т.е. должно выполняться условие неотрицательности переменных (7).

Цель данной задачи - добиться минимальных затрат на дневной рацион. Общую стоимость рациона можно выразить в виде линейной функции L=4x₁+6x₂ (коп.). Задача является многовариантной, x₁ и x₂ могут принимать бесконечное множество значений. Из этого множества следует выбрать такие x₁ и x₂, при которых функция L принимает минимальное значение. Т.о. необходимо найти минимальное значение линейной функции L=4x₁+6x₂ при ограничениях (6-7)

Еще один пример задачи о смеси: Бензины разных сортов получают путем смешивания нефтепродуктов, имеющие различные технические характеристики. Заданные показатели качества бензина (октановое число, степень очистки и др.) должны выдерживаться весьма точно, т.к. для потребителя они играют важную роль. От того, какие нефтепродукты при этом смешиваются, зависит рентабельность производства. Требуется найти такие пропорции смешивания нефтепродуктов, которые обеспечивали бы максимальную рентабельность производства и позволяли в то же время получать бензины заданных сортов в нужных пропорциях.