Расчет на динамическую нагрузку

Рекомендуемая литература

Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. М.: Высш. шк., 1995. Гл. 17.

Гастев В. А. Краткий курс сопротивления материалов. М.: Физматгиз, 1977. Гл. 14.

Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 14.

Наиболее часто встречающимися динамическими нагрузками являются:

· силы инерции, возникающие при движении тела с ускорением, в том числе в процессе колебаний элементов конструкций;

· ударные нагрузки, т. е. нагрузки, прикладываемые за очень короткий промежуток времени;

· циклические нагрузки, меняющиеся во времени по определенному циклу.

Расчет на циклические нагрузки, связанный с появлением нового свойства материалов – усталости, рассмотрен в п. 5.3.2 гл. 5 при решении задачи № 33 о проверке прочности коленчатого вала. Определению динамических усилий в стержневых конструкциях, возникающих в процессе вынужденных колебаний, посвящен разд. 7.1. Расчет на ударные нагрузки приведен в разд 7.2.

ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ (ЗАДАЧА № 37)

Рекомендуемая литература

Феодосьев В. И. Сопротивление материалов. М.: Наука, 1970. Гл. ХV (§ 101–104).

Строительная механика. Под ред. Даркова А. В. М.: Высшая школа, 1976. Гл 15.

Основные определения

Свободные (собственные)колебания – это колебания системы после сообщенного ей начального импульса. Их частота зависит от упругих свойств системы, и при наличии сил сопротивления собственные колебания постепенно затухают. Вынужденныеколебания происходят под действием возмущающих внешних сил. При изучении колебаний упругие системы различают по числу степеней свободы, то есть по числу независимых координат, определяющих положение системы. На рис. 7.1 изображена балка с колеблющейся массой m. Если массой самой балки можно пренебречь по сравнению с колеблющейся массой, то эта система имеет одну степень свободы, так как положение массы полностью определяется ее вертикальной координатой[20].

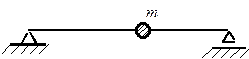Рис. 7.1. Система с одной степенью свободы

Для систем с одной степенью свободы круговая частота свободных колебаний, то есть число колебаний за 2p секунд, определяется по формуле

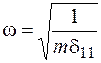, (7.1)

где 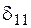– перемещение сечения с сосредоточенной массой 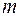по направлению ее возможного движения, вызванное единичной силой, приложенной в том же сечении и по тому же направлению. Для определения этого перемещения обычно используется метод Максвелла – Мора.

Если на систему с одной степенью свободы действует возмущающая сила, изменяющаяся по гармоническому закону 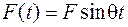и создающая вынужденные колебания системы с частотой 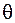, то возникающая при движении массы сила инерции тоже меняется по гармоническому закону 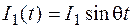. Если точка приложения возмущающей силы не совпадает с сосредоточенной массой (рис. 7.2), то, пренебрегая силами сопротивления, амплитудное значение силы инерции можно найти по формуле

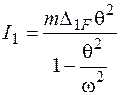, (7.2)

где 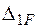– статическое перемещение сечения, в котором расположена сосредоточенная масса, по направлению ее возможного движения, вызванное амплитудным значением заданной нагрузки 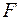. Это перемещение ищется, как правило, по методу Максвелла – Мора. Из формулы (7.2) видно, что, когда частота собственных колебаний 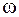равна частоте вынужденных колебаний 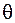, амплитуда силы инерции (а стало быть, и амплитуда перемещения массы) стремится к бесконечности. Это известное в физике явление называется резонансом.

Предполагаем, что частота вынужденных колебаний достаточно далека от частоты собственных колебаний и система работает упруго. В этом случае максимальное значение изгибающего момента (изгибающего момента от динамического действия нагрузки) можно найти, используя принцип независимости действия сил:

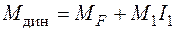. (7.3)

Формула (7.3) показывает, что изгибающий момент от динамического действия нагрузки 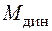равен сумме момента, вызванного статическим действием амплитуды возмущающей нагрузки 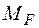, и момента от амплитудного значения силы инерции 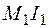. ( 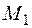– изгибающий момент от единичной силы, приложенной в сечении, где расположена масса, и направленной по направлению ее возможного движения.) Напряжения в конструкции от динамического действия нагрузки меняются пропорционально величине внутренних усилий.

Примечание. В частном, наиболее часто встречающемся случае, когда точка расположения массы и точка приложения динамической нагрузки совпадают, 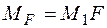и 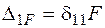. Тогда динамические усилия можно определить через статические усилия и динамический коэффициент :

,

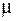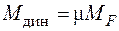где

.
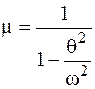