Жылдамдықтарды қосу туралы теорема

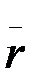Бізге күрделі қозғалыстағы М нүктесі берілсін. Осының алдында айтқанымыздай бұл нүктенің қозғалмайтын жүйеге қарағандағы орны -радиус-векторымен, ал қозғалмалы жүйеге қарағанда -радиус-векторымен анықталып отыратын болсын. Сонда:

= ₀ + , (2.113)

мұндағы ₀ полюс үшін алынған О нүктесінің радиус векторы.

Анықтама бойынша нүктенің абсолют жылдамдығы 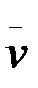_а , оның радиус векторынан уақыт бойынша алынған абсолют туындысына тең:

(2.114)

мұндағы бірінші қосылғыш О –полюстің абсолют жылдамдығын,

(2.115)

береді, ал екінші қосылғыш нүктенің полюске қатысты радиус–векторының абсолют туындысын өрнектейді.

Сондықтан:

, (2.116)

мұндағы ω-қозғалмалы Oxyz санақ жүйесінің бұрыштық жылдамдығы. Салыстырмалы туынды:

. (2.117)

(2.117) нүктенің салыстырмалы жылдамдығын береді. (2.117) –теңдікті (2.116)–ғы орнына қойсақ мынадай формула шығады:

. (2.118)

Енді (2.115) және (2.118) теңдіктері арқылы (2.114) –теңдікті соңғы түріне келтіреміз:

. (2.119)

(2.119)–формула қозғалушы нүкте М-нің абсолют жылдамдығын өрнектейді.

Қозғалушы нүктені қозғалмалы жүйеге ойша бекітілген деп жоримыз, яғни 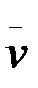_r = 0. Сонда М нүктесі қозғалмалы жүйемен тек тасымалданады. Бұл жағдайда (2.101) –формуладан мынадай формула шығады:

(2.120)

Қозғалушы М–нің абсолют жылдамдығы өрнектейтін (2.120) формуланы ықшамдалған түрге келтіреміз:

(2.121)

(2.121)–формула жылдамдықтарды қосу туралы теореманы береді.

Теорема: нүктенің абсолют жылдамдығы тасымал және салыстырмалы жылдамдықтардың векторлық қосындысына тең болады.

Мысал. Вертикаль өсті w=10с^–1 бұрыштық жылдамдықпен айнала қозғалатын , центрден тепкіш Уатта реттегішінің шарлары, машина күшінің өзгеруіне байланысты осы өстен алшақтайды және қарастыратын орнында бұрыштық жылдамдығы w₁=1.2с^–1. Берілгені: =50см, 2e=10см, a₁=a₂=a=30°. Қарастыратын уақыт мезгілінде реттегіш шарларының абсолют жылдамдығын табу керек.

Шешуі: Қозғалмалы санақ жүйесін реттегіштің өсті айнала қозғалатын бөлшектерімен байланыстырамыз. Шарлардың тасымал қозғалысы, олардың w_е=w=10с^–1 бұрыштық жылдамдықпен вертикаль өсті айнала қозғалысы , ал салыстырмалы қозғалысы, шарлардың сырықтарымен бірге олардың w_r=w₁=1.2с^–1 бұрыштық жылдамдықпен ілінетін өсті айнала қозғалыста болады.

2.32-сурет.

Әрбір шардың центрінің тасымал қозғалыс траекториясы, центрі реттегіш өсінің бойында жататын горизонталь шеңбер болады. Салыстырмалы қозғалыс траекториясы, центрі сырық ілінетін өстің бойында болатын және регулятордың жазықтығында жататын радиусы -ге тең шеңбер доғасы.

Тасымал қозғалыс шеңберінің радиусы:

см.

Шар центрінің абсолют жылдамдығы тасымал және салыстырмалы жылдамдықтардың геометриялық қосындысына тең (2.32-сурет):

, сәйкес траекторияларына жанама бойымен бағытталады, ал шамалары:

Жылдамдықтар және өзара перпендикуляр, сондықтан, векторының шамасы мынаған тең:

Шар центрінің абсолют жылдамдығы тасымал және салыстырмалы жылдамдықтардың геометриялық қосындысына тең (2.32-сурет):

, сәйкес траекторияларына жанама бойымен бағытталады, ал шамалары:

Жылдамдықтар және өзара перпендикуляр, сондықтан, векторының шамасы мынаған тең:

.

2.4.3. Үдеулерді қосу туралы теорема (Кориолис теоремасы)

М нүктесінің 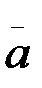_a-абсолют үдеуін қарастырайық. Аңықтама бойынша нүктенің абсолют үдеуі абсолют туындығы тең:

. (2.122)

Тасымал жылдамдық және салыстырмалы жылдамдықтан уақыт бойынша алынған абсолют туындыларды жеке-жеке қарастырайық:

, (2.123)

мұндағы 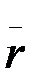радиус-векторынан уақыт бойынша алынған абсолют туындыны есептеуге мына формуланы қолданамыз:

. (2.124)

Салыстырмалы радиус-вектор 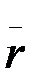-дің салыстырмалы туындысы, анықтама бойынша салыстырмалы жылдамдықты береді:

, (2.125)

(2.122) теңдікті ескере отырып, (2.124), (2.125)–теңдіктерді (2.123)–дегі орнына қоямыз. Сонда (2.122)–теңдіктен тасымал жылдамдықтан уақыт бойынша алынған абсолют туындыны өрнектейтін формула аламыз:

.

(2.122)–теңдіктің оң жағындағы екінші қосылғыш вектор салыстырмалы жылдамдықтан уақыт бойынша алынған абсолют туынды. Ал салыстырмалы жылдамдық өзінің қозғалмалы координаттар жүйесі өстеріндегі проекциялары арқылы мына түрде беріледі:

.

Сондықтан да d _r/dt-ны есептеуге өрнектейтін формуланы қолдана аламыз:

. (2.126)

(2.125) және (2.126)–теңдіктерді пайдалана отырып, (2.122)–теңдіктен мына түрдегі формулаға келеміз:

. (2.127)

(2.127)–теңдік іздеп отырған М нүктесінің абсолют үдеуінің өрнегін береді. Бұл үдеуді, кейде күрделі қозғалыстағы М нүктесінің толық үдеуі деп те атаймыз.

(2.127)–теңдіктің оң жағындағы қосылғыштардың кинематикалық мазмұндарын ашайық.

Егер = 0, 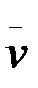₀ = 0 болса, онда (2.127)–теңдік осы жағдайда мынадай түрге келеді

. (2.128)

Егер болса, онда:

. (2.129)

Соңғы теңдіктегі полюс О-ның үдеуін белгілейді. (2.129)–теңдік, нүктенің тасымал жылдамдығы _e-нің тасымал қозғалыс кезіндегі өзгеру тездігін сипаттайды. Оны тасымал үдеу дейміз.

Зерттеп отырған (2.122)–теңдіктің оң жағында әлі аты аталмаған, екі еселенген векторлық көбейтінді түріндегі бір қосылғыш қалды. Оны 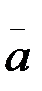_с-деп белгілейік:

. (2.130)

(2.130)–формуламен есептелінетін толық үдеудің құраушысын Кориолис деп атайды. Қабыл алынған (2.128), (2.129) (2.130) белгілеулері арқылы (2,122)–теңдікті ықшамдап жазуға болады:

. (2.131)

(2.131)–теңдікті Кориолистің үдеулерді қосу теоремасы деп атаймыз:

Кориолис теоремасы: Нүктенің абсолют үдеуі тасымал, салыстырмалы және Кориолис үдеулерінің геометриялық қосындысына тең болады.