Задачи для самостоятельного решения. 1.7.2.1. Функция. Функция f(n) определена следующим образом:
1.7.2.1. Функция. Функция f(n) определена следующим образом:
f(0)=0, f(1)=1, f(2n)=f(n), f(2n+1)=f(n)+f(n+1). Написать программу, которая по заданному натуральному числу N определяет значение функции f(N). Вводится число N (1 <= N <= 2147483647). Вывести значение f(N).
Исходные данные:
Результат:
1.7.2.2. Лесенка. Лесенкой называется набор кубиков, в котором каждый более верхний слой содержит кубиков меньше, чем предыдущий. Написать функцию, вычисляющую число лесенок, которое можно построить из N кубиков. Параметр функции натуральное число N (1 ≤ N ≤ 100) – количество кубиков в лесенке. Вывести число лесенок, которые можно построить из N кубиков.
Исходные данные:
Результат:
1.7.2.3. Задача Иосифа Флавия. Выстроим в круг N человек, пронумерованных числами от 1 до N, и будем исключать каждого k-ого до тех пор, пока не уцелеет только один человек.
Например, если N=10, K=3, то сначала умрет 3-й, потом 6-й, затем 9-й, затем 2-й, затем 7-й, потом 1-й, потом 8-й, за ним - 5-й, и потом 10-й. Таким образом, уцелеет 4-й.
Написать функцию, которая по заданным N и K (параметры) будет определять номер уцелевшего человека.
Исходные данные:
10 3
Результат:
1.7.2.4. Написать рекурсивную функцию для быстрой сортировки целочисленного массива. Параметры: массив целых чисел и два индекса – начало сортируемого куска и его конец.
1.7.2.5. Для заданного «счастливого» числа найти следующее за ним по возрастанию. Счастливое число состоит только из цифр 4 и 7. Функция получает в качестве первого параметра длинное число (в массиве находятся цифры этого числа) и его длину во втором параметре. Результат поместить в тот же массив и вернуть ИСТИНУ. Если результат не умещается в этом массиве, вернуть ЛОЖЬ.
Исходные данные:
47477 5
Результат:
1.7.2.6. Написать функцию для слияния двух упорядоченных массивов. Параметры – сами массивы и их размеры.
1.7.2.7. Написать функцию для вычисления количества слов в тексте. Параметр – строка, содержащая текст из последовательности слов.
1.7.2.8. Написать функцию для перемножения двух прямоугольных матриц. Параметры – сами матрицы и их размеры. Результат возвращается через созданную динамическую матрицу. Проверку правильности задания размеров не выполнять.
1.7.2.9. Найти корень функции методом деления отрезка пополам. Имеется описание непрерывной на отрезке [a, b] функции со значениями разных знаков на концах это отрезка. Написать функцию для вычисления корня этой функции методом деления пополам. Параметры – два вещественных числа – концы отрезка. Результат – вещественное число.
1.7.2.10. Вычисление площади по формуле Симпсона (трапеций). Имеется описание непрерывной на отрезке [a, b] функции. Написать функцию для вычисления площади фигуры, ограниченной этой функцией и осью Х. Параметры – два вещественных числа – концы отрезка. Результат – вещественное число.
1.7.2.11. Вычисление корня квадратного по итерационной формуле Ньютона. Написать функцию с одним параметром – положительным вещественным числом. Результат – корень из этого числа.
1.7.2.12. Интерполяция с помощью полинома Лагранжа. Дан массив значений аргумента x1, x2, ..., xn и массив значений некоторой функции в этих точках f1, f2, ..., fn. Написать функцию для вычисления значения этой функции в некоторой точке Х. Параметрами функции являются вещественные массивы x, f, число точек n и значение аргумента Х.
Продвинутые задачки.
1.7.3.1. Перестановки. Написать функцию для генерации очередной перестановки в лексикографическом порядке. Функция получает в качестве первого параметра перестановку (в массиве находятся её элементы) и длину перестановки n во втором параметре. Результат поместить в тот же массив и вернуть ИСТИНУ. Если следующей перестановки нет, вернуть ЛОЖЬ.
Исходные данные:
45132 5
Результат:
1.7.3.2. Написать функцию (с рекурсией и без нее) для вычисления функции Аккермана:
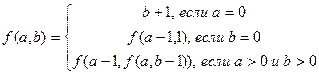
Параметры функции неотрицательные целые числа.
Исходные данные:
2 3
Результат:
1.7.3.3. Ханойские башни. Имеется 3 вертикальных штырька. На первый из них нанизаны N колец одно поверх другого, причём ни одно кольцо большего радиуса не находится поверх кольца меньшего радиуса. Два других штырька пустые. За один ход разрешается переставить верхнее кольцо с любого штырька на другой штырёк, но запрещается поверх малого кольца помещать кольцо большего радиуса. Написать программу, которая выведет кратчайшую последовательность перемещений колец с первого штырька на второй. Вывод оформить так, как это показано в примере. В первой строке вывести количество операций, а в остальных – сами операции.
Исходные данные:
Результат:
1 -> 2
1 -> 3
2 -> 3
1 -> 2
3 -> 1
3 -> 2
1 -> 2
1.7.3.4. Дано натуральное число N. Найти наименьшее натуральное число M, сумма цифр которого равна N.
Исходные данные:
Результат:
Тема 1.8. Автоматы
Цель.
Основные понятия.
Ключевые слова.
Автомат, диаграмма состояний
ПРИМЕР.
Алгоритм.
Решение.
