Поняття первісної функції та невизначеного інтеграла
Нехай функція f(x) визначена на деякому проміжку Х.
Означення. Функція F(x) називається первісною для функції f(x) на деякому проміжку Х, якщо F(x) диференційована на проміжку Х, причому виконується рівність F'(x) = f(x).
Теорема. Нехай F1(x) і F2(x) – довільні первісні для функції f(x) на проміжку Х, тоді F1(x) - F2(x)= сonst =C. Тобто дві первісні відрізняються одна від одної лише на сталу величину.
Доведення:
Нехай F1(x) і F2(x) первісні для функції f(x) на проміжку Х 
F1’(x) - F2’(x)= f(x) за означенням.
Позначимо F1(x) - F2(x)=λ(x).
Знайдемо похідну λ’(x) = F1’(x) - F2’(x) = f(x)- f(x)=0 (на проміжку Х).
А тоді з теореми про необхідну і достатню умову сталості функції одержимо, що λ(x)= сonst =C F1(x) - F2(x) = C.
Наслідок.Якщо F(x)- одна з первісних для функції f(x) на проміжку Х, то будь-яку іншу первісну Ф(x) цієї функції на цьому ж проміжку можна подати в такому вигляді Ф(x)=F(x)+C, де С – деяка стала.
Означення. Сукупність всіх первісних для функції f(x) на деякому проміжку Х називається невизначеним інтегралом функції f(x) на деякому проміжку Х і позначається 
, х- змінна інтегрування,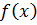 
- підінтегральна функція, 
- підінтегральний вираз, 
- знак інтеграла.
Таким чином має місце рівність: = F(x)+С, де F(x) – одна з первісних для функції 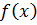, С – будь-яка стала.
Приклад 1. 
,
= 
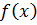, F(x) = 
, F'(x)= ( 
Властивості невизначеного інтеграла
1. 
Тобто знак диференціала і інтеграл взаємоскорочувані, якщо знак диференціала стоїть поперед знака інтеграла.
Оскільки $ , то виконується рівність (1) = F(x)+С (α), де F'(x) = f(x) (β).
.
2. 
.
3.Лінійна властивість 
,
[ 
= 
= 
4.Лінійна властивість 
= c , (c - const)
Доведення аналогічно вл. 3.
Таблиця інтегралів для деяких елементарних функцій
   (        |          |
Найпростіші правила інтегрування
1.Якщо 
(1), то 
З (1) 
F’(t) = f(t), З (2) [ 
]’= 
F’( 
) 
= f( )
Приклад 1.
.
.
2. 
[ 
]’ = 
Приклад. 
{ 
+ C.
Зауваження:
Інтеграли від елементарної функції не завжди можна виразити через елементарні функції. Якщо інтеграл вдається виразити через елементарні функції, то кажуть, що дана функція інтегрується в скінченому вигляді або в елементарних функціях.
Інтеграли, що не мають значень:
Інтеграл Пуасона: 
; Інтеграли Френеля: 
, 
, 
, 
, 
.
Метод інтегрування частинами
Теорема. Нехай функції u(x) i v(x) диференційовані на деякому проміжку Х. Якщо існує первісна для функції v(x)* u’(x) на Х (тобто $ 
або у скороченому вигляді 
(1’)
Доведення. Розглянемо 
. Застосуємо правило обчислення похідної: [ ]’ = 
+ 
(2)
Оскільки за умовою теореми $ 
, крім того за властивістю 1 невизначеного інтеграла 
= 
$ 
. Тоді з рівності (2) одержимо формулу (1) (Беручи до уваги, що це рівність множин).
Приклад. 
Метод заміни змінної
Теорема. Нехай виконуються умови:
1) Функція t=φ(x) визначена і диференційована на проміжку Х, Т – множина значень функції φ(x).
2) Функція g(t) має первісну G(t) на T (тобто $ 
, тоді скалярна функція 
– первісна 
на Х. 
(1).
Доведення. Нехай умови теореми виконані.
Знайдемо похідну правої частини формули (1) [ 
]’= G’( 
.
Застосування. В багатьох випадках вдається підібрати t= 
, так що виконується рівність f(x)dx = 
. Причому 
.
Достатньо просто обчислити, будемо вважати, що 
. Тоді маємо 
= 
= 
Приклад. 
= 
Іноді заміну змінної проводять безпосередньо
Припустимо, що інтеграл вдалось знайти і він має вигляд 
Приклад. 
= 