Басқару шамалары автоматты басқару жүйелері

Реттелетін шамалардың объектіде берілген деңгейде ұстап тұру үшін немесе оларды берілген заңдылық бойынша өзгерту үшін реттегіштер мен қосымша құрылғылар орнатылады, олар реттелетін объектімен бірге реттелетін шамасы бірнеше автоматты реттеу жүйесін тудырады.

Реттелетін шамалары бірнеше жүйелер байланыспаған және байланысты реттеу жүйелеріне бөлінеді. Байланыспаған реттеу жүйелері дегеніміз әртүрлі шамаларды реттеуге арналған реттегіштері бір – бірімен байланыспаған және тек өздеріне ортақ реттелетін объект арқылы ғана өзара әрекет етуі мүмкін жүйелерді айтамыз.

Байланыспаған реттеу жүйелері тәуелді және тәуелсіз болып бөлінеді.

Тәуелді деп кез – келген реттелетін шаманың өзгерісі өзінен кейін барлық қалған реттелетін шамалардың өзгеруіне алып келетін жүйелерді айтамыз. Мысалы, қазандағы су деңгейінің өзгерісі өзінен кейін бу қысымы мен температурасының өзгеруіне алып келеді; бу қысымының өзгерісі өзінен кейін су температурасы мен деңгейінің өзгеруіне алып келеді.

Тәуелсіз деп кез – келген бір реттелетін шаманың өзгерісі басқа реттелетін шамалардың өзгеруін тудырмайды. Мысалы, жеке жұмыс істеп жатқан генератордың кернеуінің өзгерісі өзінен кейін айнымалы ток жиілігінің өзгеруін болдырмайды.

Тәуелсіз жүйелердегі жеке шамаларды реттеу процестерін оқшаулана қарастыруға болады, оларды реттелетін шамасы біреу жүйелер үшін алдыңғы тарауларда берілген әдістермен синтездеуге және талдауға болады.

Байланысты реттеу жүйелері деп әртүрлі реттелетін шамалардың реттегіштері бір – бірімен және реттелетіні объектімен бірге конструктивті түрде байланысатын жүйелерді айтамыз.

Байланысқан реттеу жүйелері мен байланыспаған реттеудің тәуелді жүйелері, яғни реттелетін шамалар бір – бірімен байланысқан барлық жүйелер көпбайланысты реттеу жүйесі деп аталады. Бұл жүйелерге келесі анықтама берілуі мүмкін.

Көпбайланысты деп бір – бірімен реттеуші объект, реттегіш немесе жүктеме арқылы байланысқан бірнеше реттелетін шамалары бар автоматты реттеу жүйелерін айтамыз.

Байланысты реттеу жүйелеріндегі реттегіштер арасындағы байланыстар әртүрлі түрде тұрғызылуы мүмкін. Бұл байланыстар шамалардың кез – келгені өзгерген кезде олардың арасында тұрақты қатынасты қамтамасыз ете алады, барлық реттелетін шамалардың кез – келгені өзгерген кезде реттеу автономдығын қамтамасыз ете отырып өзгермейтіндігін де қамтамасыз ете алады.

Автономды реттеу жүйесі дегеніміз реттеу процесінде бір реттелетін шаманың өзгерісі басқа реттелетін шамалардың өзгеруін тудырмайтын реттегіштер арасындағы байланыстары бар көпбайланысты жүйені айтамыз.

Көпбайланысты жүйелерді бір реттелетін шамасы бар жүйелердің қарапайым қосындысы ретінде қарастыруға болмайды. Көпбайланысты жүйелерге арнайы теория өңделіп шығарылған, онда осындай жүйелерді зерттеудің арнайы әдістері ұсынылады. Көпбайланысты жүйелерді зерттеу негізінде қойылған принциптерді қарастырайық.

Көпбайланысты автоматты реттеу жүйе объектілерінде әрбір реттелетін шамасы бойынша өзінің жеке шығыс бар. Кіріс саны шығыс санынан кіші болуы тиіс, кейбір жағдайларда кірістер шығысқа қарағанда көп болуы мүмкін, әрбір реттелетін шама бойынша өзінің реттеу жүйесі пайда болады және осы кезде әрбір реттелетін шамаға бір орындаушы орган мен бір реттегіш сәйкес келуі тиіс. Реттелетін объект санымен қатар сыртқы әсерлерге душар болады, олар барлық немесе тек кейбір реттелетін шамаға әсер етеді. Одан бөлек, көпбайланысты жүйенің барлық реттелетін шамалары бір – бірімен өзара әрекет етеді. Көпбайланысты жүйелердегі реттеу процесінің математикалық бейнесі жеткілікті күрделі болып шығады. Математикалық өрнектерін біршама жеңілдету үшін дифференциалды теңдеулер жүйесінің матрицалық түрде жазылуы қолданылады.

Көпбайланысты жүйенің жалпы түрдегісін қарастырайық, онда үш реттелетін шама жүзеге асырылады. 11.7. суретте реттелетін объектінің матрицалық түрдегі теңдеуі берілген. 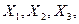шамалары кірістер, 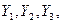– шығыстары болып табылады. Матрицаның А 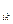әрбір элементі шығыс шаманы кіріс шамамен байланыстыратын беріліс функцияны береді. Келтірілген матрица барлық шығыс шамалар барлық кіріс шамаларымен байланысқаны шығады. Содан, мысал, 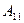беріліс функциясы 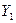шығыс шаманы 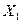–ні кіріс шамамен, ал 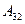беріліс функциясы 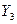пен 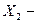ні байланыстырады. Барлық кіріс шамаларға тәуелді шығыс шаманы алу үшін кіріс шамаларды сәйкес жолдағы беріліс функцияға көбейтіп, және туындыларын қосу керек. 11.7. суреттегі объект үшін үш теңдеу жүйесін аламыз, ол Лаплас бейнесі бойынша құрылған:

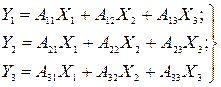(11.21)

11.8. суреттерде бір – бірімен конструктивті түрде байланысқан реттегіштердің матрица түрдегі теңдеуі көрсетілген. Кірісіне реттелтін объектінің өлшенген реттелетін шығыс шамаларының 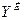мен реттелетін шаманың берілген мәні 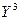–ң айырымы беріледі. Матрицаның элементтері 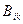реттегіштер мен олардың арасындағы байланыстың сәйкес беріліс функцияларын береді.

Реттегіштер жүйесі үшін де Лаплас бейнесі бойынша үш теңдеулер жүйесін аламыз.

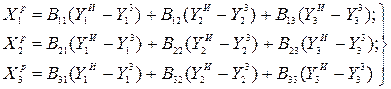(11.22)

Реттелетін шамаларды салыстыру элементтері бір – бірімен байланыспаған. Сонымен қатар 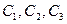беріліс функциялы реттелетін элементтер мен беріліс функциясы 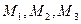өлшеу элементтері де байланыспаған.

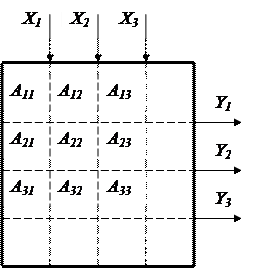
11.7. Сурет. Матрица түрдегі объектінің теңдеуі

11.9. сертетерде көпбайланысты автоматты реттеу жүйесінің матрица түрдегі функционалды схемасы берілген. Бұл схемадағы сыртқы 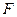әсерлері реттегіштерден келіп түсетін әсерлермен бірігеді де бірдей кіріс арқылы объектіге келіп түседі.

Реттелуші объект пен реттегіштердің теңдеулерін қысқа түрінде жазуға болады. сонда объектінің теңдеуін (11.21) былай жазуға болады.

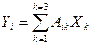(11.23)

Реттегіштің теңдеуін (11.22) мына түрде жазуға болады.

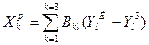(11.24)

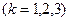
Өлшеу элементтерінің теңдеуін

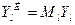(11.25)

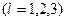
Реттеуші элементтер мен әсерлер теңдеуі

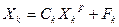(11.26)

(11.23)- (11.24) теңдеулер жүйесін реттелетін объектінің шығыс реттелуші шамаға 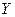қатысты шеше отырып, аламыз

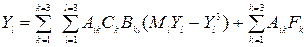(11.27)

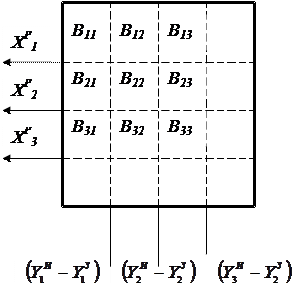
11.8. Сурет. Ретегіштердің матрица түрдегі теңдеуі

(11.27) өрнегі тұйықталған көпбайланысты автоматты реттеу жүйесінің реттелетін шамаларының шығысының біреуі үшін Лаплас бейнесінің жалпы түрдегі теңдеуін көрсетеді, ол әрбір реттелетін шама барлық басқа реттелетін шамаларға және реттелеуші объектіге келіп түсетін барлық ауытқу әсерлерге тәуелді, әрі осы шамалар арасындағы байланыс объект арқылы және реттегіштер арқылы жүзеге асады. Егер реттегіштер бір бірімен байланыспаған болса және реттелетін шамалар арасындағы байланыс тек объект арқылы жүзеге асса, (11.27) өрнектегі 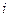бойынша қосынды белгісі жойылып кетеді де, өрнек 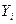үшін мына түрді қабылдайды.

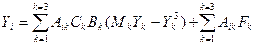(k=1, 2, 3). (11-28)

Бұл жағдайда 11.8. суретте көрсетілген реттегіштер матрицасы ыдырап кетеді, өйткені бас диагональда орналасқан 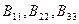реттегіштердің беріліс функциялары ғана қалады, ол реттегіштер арасындағы өзара байланыстың барлық беріліс функциялары нөльге айналып кетеді, өйткені реттегіштер арасында байланыс болмағандықтан.

Автономды жүйелер жағдайында реттегіш арасындағы байланыстар әрбір реттелетін шамаға тек оған сәйкес әсерлер ғана әрекет ететін болып шығады. Басқа реттелетін шамалар, есептер мен әсерлер қарастырылған реттегіш шамаға әсер етпейді. Бұл, егер (11.27) өрнегінде жеке, сепораторлы реттеу деп аталатын жүйеге кіретін объекті мен реттегіштердің беріліс функциясының туындылары маңызды болған жағдайда ғана мүмкін. бұл тербеліс функциялары матрицаның бас диагоналында орналасқан. ( 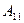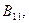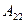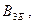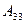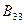). Объектідегі сепараторлық жүйелер мен реттегіштер арасындағы байланыстың беріліс функциясы кіретін барлық қалған туындылар нөльге тең болуы тиіс.

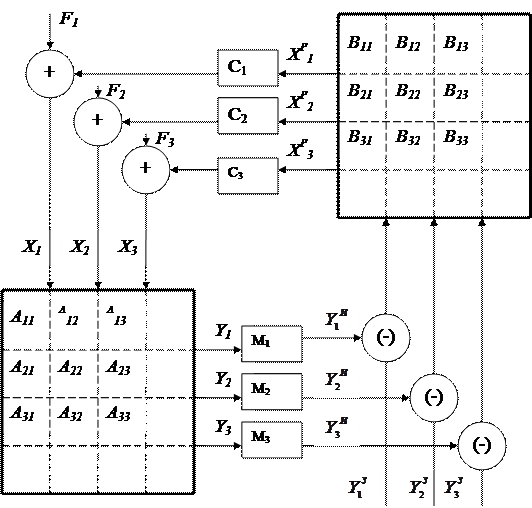
11.9. Сурет. Матрица түрдегі көпбайланысты автоматты реттеу жүйесі

(11.27) өрнегі бұл кезде үш жеке теңдеуге ыдырап кетеді, олар бір – бірімен байланыспайды:

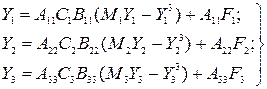(11-29)

Бұл шарт математикалық түрде тек, егер жүйенің толық матрица элементтері, бас диоганальда жатпайтын, нөльге тең болса және диагональ элементтерімен тікелей анықталатын шамалар болып табылған жағдайда ғана орындалады. Автономдық шарттары толығымен [29]–да қарастырылған.

Көпбайланысты жүйелерде сонымен қатар реттелетін шамалардың бір жағынан немесе барлық ауытқу әсерлерінен инварианнттылығының сұрақтары да шешеілуі мүмкін. бұл жағдайда сепараторлық жүйелер ауытқу бойынша және ауытқу бойынша жүйелерден құралған құрастырылған жүйе түрінде тұрғызылады.

Нақты жүйелердегі автономдық шарты инварианттылық шартын әдетте абсолютті түрде іске асыруға болмайды. олар дәлділікпен ең кіші 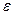шамаға дейін іске асырылады, үстемді көп жағдайларда инженерлік тәжірибе талаптарын қанағаттандырады.

Көпбайланысты автоматты реттеу жүйесіндегі тұрақтылық мәселесін шешу бір реттелетін шамасы бар жүйелердегі осы мәселені шешуге ұқсас болып табылады.

Көпбайланысты жүйе тұрақты болуы үшін оған кіретін барлық сепараторлық жүйелер тұрақты болуы қажет және жеткілікті. Егере ң болмағанда бір сепаратолық жүйесі тұрақсыз болып шығады. Тұйықталған сепараторлық жүйені тұрақтылыққа зерттеу үшін, оның сипаттамалық теңдеуін табу және Гурвиц критериясын пайдалану қажет.Ол үшін ізделіп жатқан сепараторлық жүйе үшін 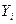шығыс реттелетін шаманың бейнесін жазып шығарған жөн, ол үшін жүйе байланысының (11.27), (11.28), немесе (11.29) сипатын пайдалана отырып, содан кейін, осы өрнекті түрлендіріп, нақты түрдегі сипаттамалық теңдеуін алған жөн және оны зерттеу қажет.

Орнатылған дәлдікті жоғарлатуға қажет болуы мүмкін бір контурлы сепараторлық жүйенің күшею коэффициенттерін жоғарлату кезінде тұрақтылық жоғалып кетуі мүмкін. Осыны болдырмау үшін сепараторлық жүйелерге икемді кері байланыс түрдегі түзеткіш құрылғылар күшейту коэффициенті үлкен элементтердің айналасына енгізіледі. Бұл аса Жоғары күшею коэффициенттерді тұрақтылықты жоғалтпай қабылдауға мүмкіндік береді. Сепараторлық жүйелерде жүйсаралық байланыстың беріліс коэффициенттерімен салыстырғанда өте үлкен күшею коэффициенттерін салыстырғанда өте үлкен күшею коэффициенттерін пайдалану көпбайланысты жүйеге дәлділігі 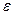кіші шамаға дейінгі автономдық қасиетін береді.

Реттеу сапасын зерттеу мағыналы, егер ол әрбір реттелетін шама бойынша жеке – жеке орндалса. Мұндай зерттеу сепараторлық жүйе теңдеуі бойынша жүргізіледі. Бұл теңдеу 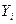реттелетін шама үшін Лаплас бейнесі бойынша алынуы мүмкін, яғни (11.27), (11.28), (11.29) теңдеулерінің біреуімен. Алынған теңдеудегі зерттелетін жүйеге келеп түсетін әсер мен басқа реттелетін шамалар жағынан келген әсерлер қарапайым әсерлер түрінде қарастырылуы мүмкін.

Бір реттеуші шамасы бар жүйе үшін өңделген әдістермен сепараторлық жүйенің реттеу сапасы зерттеледі және егер қажет болса, түзеткіш құрылғылары да синтезделеді.

Көпбайланысты реттеу жүйелерін талдау мен синтездеу сұрақтарына [29] монографиясы арналған, ол бойынша осы жүйелерді зерттеу әдістерімен аса толық танысуға боады.

Негізгі әдебиет: 3 [324-348].

Қосымша әдебиет: 1 [365-414].

Бақылау сұрақтары:

1. Реттелетін шамалары бірінші автоматты басқару жүйелерінің ерекшелігі қандай?

2. Қандай жүйелер байланыспаған, байланысты реттеу, тәуелді, тәуелсіз, көпбайланысты, автономды жүйелер деп аталады?

3. Көпбайланысты жүйедегі реттелетін шаманың өрнегін жалпы түрде қалай құру керек?

4. Сеператорлық жүйе дегеніміз не?

5. Көпбайланысты жүйелердің автономдық шарты қалай орындалады ?

6. Көпбайланысты жүйелерде тұрақтылық кіріс процесі ретінде қалай зерттеледі?