Динамическое уравнение САУ – дифференциальное уравнение

Пример:

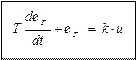Тогда дифференциальное уравнение генератора

(уравнение динамики).

Статические характеристики звеньев и объектов САУ.

Статической характеристикой по каналу управления (возмущения) объекта называется функциональная зависимость выход-вход при отсутствии или постоянном значении возмущения (управления), все точки которой сняты в установившемся режиме (при t®¥).

Возьмём для примера в качестве элемента системы полупроводниковый усилитель. Статическая характеристика усилителя имеет вид, приведенный на рис.1.

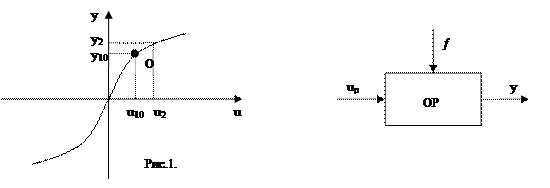Точка О – рабочая точка усилителя.

y=f(u); Δy=y-yo;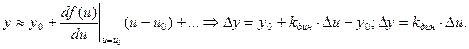

Статический передаточный коэффициент усилителя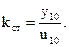

Динамический передаточный коэффициент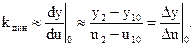

У объектов регулирования определяют статические характеристики по каналам управления и возмущения:

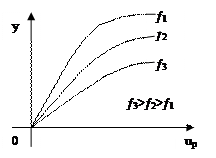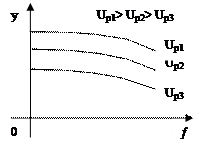Возмущение обычно Внешние характеристики объекта

действует со знаком “-”

Вопрос 2. Запасы устойчивости

Для нормального функционирования всякая САР должна быть удалена от границы устойчивости и иметь достаточный запас устойчивости. Необходимость этого обусловлена следующими причинами:

1. Уравнения элементов САР, как правило, идеализированы, при их составлении не учитывают второстепенные факторы;

2. При линеаризации уравнений погрешности приближения дополнительно увеличиваются;

3. Параметры элементов определяют с некоторой погрешностью;

4. Параметры однотипных элементов имеют технологический разброс;

5. При эксплуатации параметры элементов изменяются вследствие старения.

В практике инженерных расчетов наиболее широко используют определение запаса устойчивости на основе критерия НАЙКВИСТА, по удалению АФХ разомкнутой системы от критической точки с координатами (-1, j0), что оценивают двумя показателями: запасом устойчивости по фазе g и запасом устойчивости по модулю (по амплитуде) H.

Для того чтобы САР имела запасы устойчивости не менее g и H, АФХ ее разомкнутой цепи при удовлетворении критерия устойчивости не должна заходить в часть кольца, заштрихованного на рис. 1, где H определяется соотношением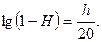

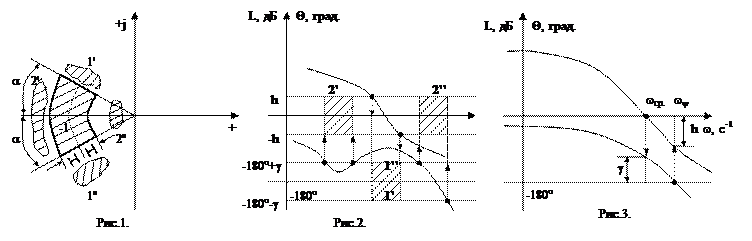
w, с-1

`

Если устойчивость определяется по ЛЧХ условно-устойчивых систем, то для обеспечения запасов устойчивости не менее g и h необходимо, чтобы:

а) при h ³ L ³ -h фазо-частотная характеристика удовлетворяла неравенствам θ > -180°+g или θ < -180°-g, т.е. не заходила в заштрихованную область 1 на рис. 2;

б) при -180°+g ³ θ ³ -180°-g амплитудно-частотная характеристика удовлетворяла неравенствам L < -h или L > h, т.е. не заходила в заштрихованные области 2' и 2'' на рис. 2.

Для абсолютно устойчивой системы запасы устойчивости g и h определяют так, как показано на рис. 3:

1. Запас по фазе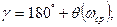

2. Запас по модулю h=-L(ω_-π), где ω_-π – частота, при которой θ=-180^˚.

Необходимые значения запасов устойчивости зависит от класса САР и требований к качеству регулирования. Ориентировочно должно быть g=30¸60° и h=6¸20дБ.

Минимально допустимые запасы устойчивости по амплитуде должны быть не менее 6дБ (то есть передаточный коэффициент разомкнутой системы в два раза меньше критического), а по фазе не менее 25¸30°.

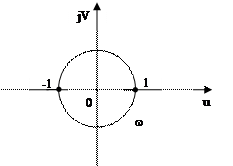
Устойчивость системы со звеном чистого запаздывания.

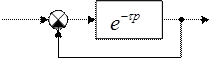Если АФХ разомкнутой системы проходит через точку (-1, j0), то система на грани устойчивости.

Систему с чистым запаздыванием можно сделать устойчивой, если в схему включить безынерционное звено с передаточным коэффициентом, меньшим 1. Возможны и другие виды корректирующих устройств.

Структурно-устойчивые и структурно-неустойчивые системы

Один из способов изменения качества системы (в смысле устойчивости) – это изменить передаточный коэффициент разомкнутой системы.

При изменении k L(w) поднимется либо опускается. Если k увеличивать, L(w) поднимается и w_ср будет возрастать, а система останется неустойчивой. Если k уменьшать, то систему можно сделать устойчивой. Это один из способов коррекции системы.

Системы, которые можно сделать устойчивыми путем изменения параметров системы, называются СТРУКТУРНО-УСТОЙЧИВЫМИ.

Для этих систем есть критический передаточный коэффициент разомкнутой системы. K_крит. – это такой передаточный коэффициент, когда система на грани устойчивости.

Существуют системы СТРУКТУРНО-НЕУСТОЙЧИВЫЕ – это такие системы, которые невозможно сделать устойчивыми изменением параметров системы, а требуется для устойчивости изменять структуру системы.

Пример.

Рассмотрим три случая: 1. Пусть 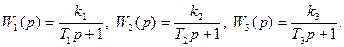Тогда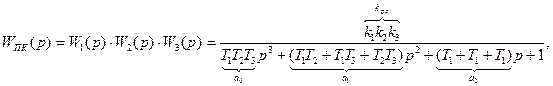

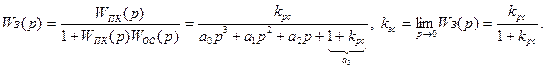
Проверим работу системы на устойчивость.

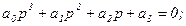
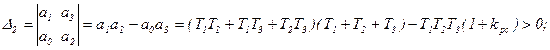
Δ=а₃Δ₂>0.

Для определения k_рс.кр. приравняем нулю D₂.

Тогда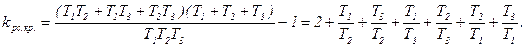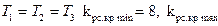

При при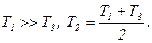

Рассматриваемая система СТРУКТУРНО-УСТОЙЧИВАЯ, так как ее можно стабилизировать путем изменения параметров звеньев.

2) Пусть 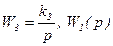и 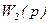те же, что в первом случае.

Теперь 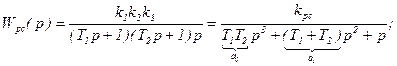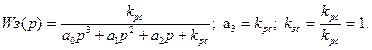Статической ошибки по каналу управления нет.

Условия устойчивости по Гурвицу:

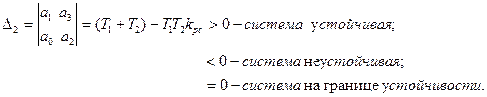
Пусть D₂=0, тогда 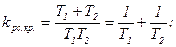если 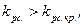то система неустойчивая.

Данная система с астатизмом 1-го порядка СТРУКТУРНО-УСТОЙЧИВАЯ.

3) 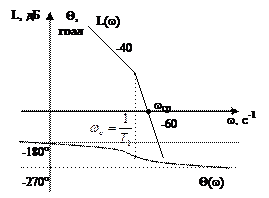Пусть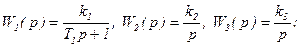

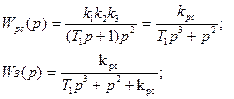
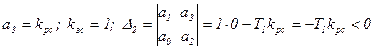всегда система неустойчива. Эта система СТРУКТУРНО-НЕУСТОЙЧИВАЯ.

Билет 23