II. Преобразования Галилея
Для того, чтобы охарактеризовать движение тел в пространстве, необходимо указать систему отсчета, относительно которой это движение происходит. Под системой отсчета в физике понимают некоторую систему тел, относительно которой рассматривается движение, снабженную часами (в качестве которых может служить любой периодический процесс).
Среди всех систем отсчета особое место занимает инерциальные системы отсчета (ИСО), т.е. такие, в которых справедлив закон инерции Ньютона. Особая роль ИСО связана с тем, что в них движение имеет наиболее простой вид. Из классической механики известно, что радиус-вектор 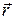 и скорость
и скорость 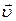 материальной точки относительно некоторой ИСО
материальной точки относительно некоторой ИСО 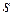 связаны с радиус-вектором
связаны с радиус-вектором 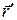 и скоростью
и скоростью 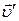 относительно системы
относительно системы 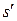 , не ускоренно движущейся по отношению к
, не ускоренно движущейся по отношению к 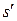 соотношениями:
соотношениями:
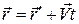 (1а)
(1а)
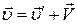 (1б)
(1б)
Здесь 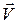 - постоянный вектор, и для простоты предполагается, что в начальный момент времени
- постоянный вектор, и для простоты предполагается, что в начальный момент времени 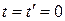 начала обеих систем совпадали. Напомним, что в классической механике:
начала обеих систем совпадали. Напомним, что в классической механике:
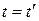 (1в)
(1в)
Из формулы (1б) заключаем, что
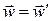 (2)
(2)
где 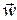 и
и 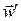 - ускорение относительно
- ускорение относительно 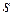 и
и 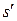 . Т.е. если ускорение изолированной точки равна нулю относительно
. Т.е. если ускорение изолированной точки равна нулю относительно 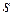 , то оно равно нулю и относительно
, то оно равно нулю и относительно 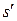 . Следовательно, для любых
. Следовательно, для любых 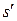 движущееся не ускоренно относительно
движущееся не ускоренно относительно 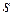 тоже инерциальная СО.
тоже инерциальная СО.
Таким образом преобразования (1а) – (1в) описывают переход от одной ИСО к другой. Они называются преобразованиями Галилея. Формула (1б) носит название закона сложения скоростей.
На основании обобщения опытных данных Галилей сформулировал следующий классический принцип относительности: Законы механики одинаковы в любой ИСО. Или другими словами законы классической механики инвариантны относительно преобразований Галилея. Это, в частности, означает, что никакими экспериментами нельзя обнаружить факт абсолютного движения. Термины “покой” и “равномерное и прямолинейное движение” имеет относительный характер. Понятие же абсолютного же движения и покоя не имеет реального содержания.
Замечание: создатель классической механики Ньютон доказал возможность обнаружения такого движения. Он считал, что движение или покой могут иметь место в абсолютном пространстве, существующем само по себе, безотносительно к чему-либо.
Взгляды на абсолютное пространство, как на некоторую исходную привилегированную СО продержались до начала нашего века (в виде различных модификаций теории мирового эфира).
