Простіше зразу шукати послідовні суми !
18. Діагоналі вписаного чотирикутника 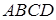 перетинаються в точці
перетинаються в точці 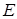 , при цьому
, при цьому 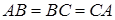 ,
, 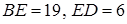 . Які значення може набуваати довжина сторони
. Які значення може набуваати довжина сторони 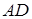 ?
?
Відповідь: 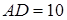 або
або 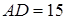 .
.
Розв’язання. З теореми Птолемея запишемо, що
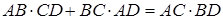 ,
,
звідки 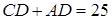 . Позначимо
. Позначимо 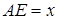 ,
, 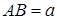 , тоді з подібностей трикутників маємо:
, тоді з подібностей трикутників маємо: 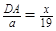 та
та 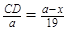 . Тоді
. Тоді 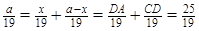 , або
, або 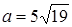 . З теореми синусів:
. З теореми синусів: 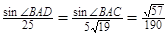 , звідки
, звідки 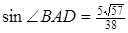
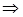
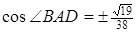 . Тепер з теореми косинусів знаходимо, що
. Тепер з теореми косинусів знаходимо, що 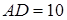 або
або 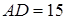 .
.
19.Знайдіть всі натуральні числа, взаємно прості с усіма членами нескінченної множини чисел: 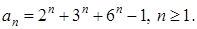
Відповідь: 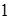 .
.
 Розв’язання.Покажемо, що
Розв’язання.Покажемо, що 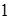 єдине таке число. Досить довести, що для кожного простого числа
єдине таке число. Досить довести, що для кожного простого числа 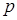 існує деяке
існує деяке 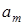 таке, що
таке, що 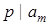 . Для
. Для 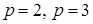 ми маємо, що
ми маємо, що 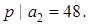 Тепер припустимо, що
Тепер припустимо, що 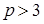 . Спираючись на теорему Ферма, ми маємо:
. Спираючись на теорему Ферма, ми маємо: 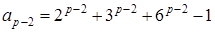 , звідки випливає, що
, звідки випливає, що
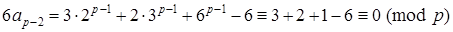 .
.
Отже 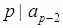 , що й треба було довести.
, що й треба було довести.
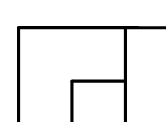
20.Деякий прямокутник розрізаний на непарну кількість однакових багатокутників (однакові – означає, що їх можна накласти один на інший, можливо з перегортанням). Чи обов’язково ці багатокутники – прямокутники?
Відповідь: не обов’язково, один з прикладів такого розрізання показаний на рис. 8.
 21.Доведіть, що одиничний квадрат можна покрити деякими трьома множинами з діаметрами не менше ніж
21.Доведіть, що одиничний квадрат можна покрити деякими трьома множинами з діаметрами не менше ніж 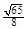 , але не можна покрити ніякими множинами з діаметрами менше ніж
, але не можна покрити ніякими множинами з діаметрами менше ніж 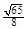 . (Діаметром множини називається відстань між двома найвіддаленішими точками цієї множини)
. (Діаметром множини називається відстань між двома найвіддаленішими точками цієї множини)
Розв’язання. Розглянемо три кола діаметром 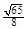 з центрами у точках
з центрами у точках 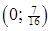 ,
, 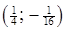 та
та 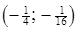 (рис. 9), тоді неважко переконатись, що вони покривають квадрат з вершинами у точках
(рис. 9), тоді неважко переконатись, що вони покривають квадрат з вершинами у точках 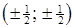 .
.
Тепер друга частина задачі. Методом від супротивного, припустимо що одиничний квадрат 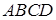 повністю покритий трьома фігурами
повністю покритий трьома фігурами 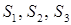 з діаметрами меншими від
з діаметрами меншими від 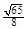 . Тоді принаймні дві вершини, наприклад,
. Тоді принаймні дві вершини, наприклад,  покриваються однією множиною, наприклад,
покриваються однією множиною, наприклад,  , тоді з визначення діаметра множини інші дві вершини квадрату не покриті цією множиною.
, тоді з визначення діаметра множини інші дві вершини квадрату не покриті цією множиною.
 Якщо
Якщо 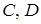 покриті однією множиною, наприклад,
покриті однією множиною, наприклад, 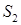 , то розглянемо ребро
, то розглянемо ребро 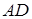 і
і 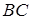 та їх середини відповідно точки
та їх середини відповідно точки 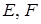 (рис. 10). Оскільки
(рис. 10). Оскільки 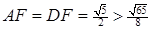 , то точка
, то точка 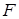 (аналогічно й
(аналогічно й 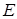 ) можуть бути покриті лише множиною
) можуть бути покриті лише множиною 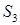 . Але, оскільки для точки
. Але, оскільки для точки 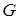 – середини відрізку
– середини відрізку 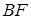 маємо, що
маємо, що 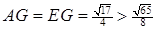 , то вона не може бути покритою жодною з трьох множин
, то вона не може бути покритою жодною з трьох множин 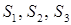 . Таким чином це припущення хибне.
. Таким чином це припущення хибне.
Тому залишається варіант, коли точка 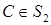 , а точка
, а точка 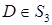 . Тоді точка
. Тоді точка 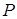 , що задовольняє умову
, що задовольняє умову 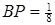 та
та 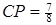 може бути покритою лише множиною
може бути покритою лише множиною 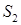 , бо
, бо 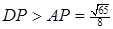 (рис. 11). Але для точки
(рис. 11). Але для точки 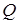 , що є серединою
, що є серединою 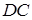 виконуються умови:
виконуються умови: 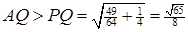 . Тому вона повинна покриватися лише множиною
. Тому вона повинна покриватися лише множиною 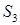 , але з симетричних міркувань, вона нею покриватися не може. Твердження доведене.
, але з симетричних міркувань, вона нею покриватися не може. Твердження доведене.
22.На стороні 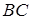 трикутника
трикутника 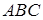 вибрані точки
вибрані точки 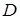 та
та 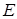 , для яких виконуються такі умови:
, для яких виконуються такі умови: 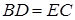 та
та 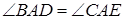 . Доведіть, що
. Доведіть, що 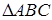 рівнобедрений.
рівнобедрений.
 Розв’язання. Оскільки
Розв’язання. Оскільки 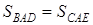 (однакові висоти та основи), то
(однакові висоти та основи), то 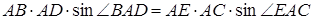 . Тому
. Тому 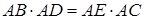 (рис. 12).
(рис. 12).
Аналогічно, оскільки 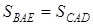 , то
, то 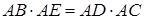 .
.
Якщо перемножимо останні дві рівності, маємо:
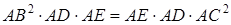 ,
,
звідки й маємо шукану рівність: 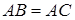 .
.
23.Знайдіть найбільше та найменше значення виразу
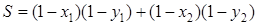
для дійсних чисел 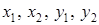 , що задовольняють умову:
, що задовольняють умову: 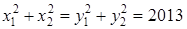 .
.
Відповідь: найбільше 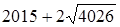 , найменше
, найменше 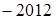 .
.
Розв’язання. Позначимо через 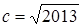 , тоді можемо позначити невідомі таким чином:
, тоді можемо позначити невідомі таким чином:
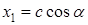 ,
, 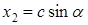 ,
, 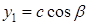 ,
, 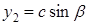 . Тоді
. Тоді
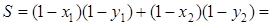
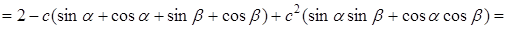
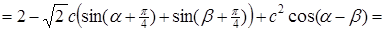
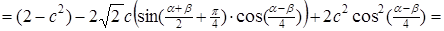
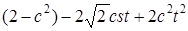 ,
,
де 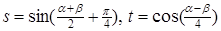 .
.
Внаслідок незалежності 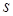 та
та 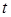 – ці змінні можуть приймати будь-які значення на проміжку
– ці змінні можуть приймати будь-які значення на проміжку 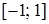 . Тоді зрозуміло, що найбільше значення:
. Тоді зрозуміло, що найбільше значення:
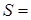
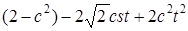
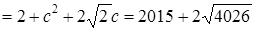 ,
,
при 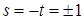 або
або 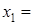
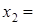
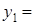
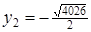 .
.
Аналогічно, найменше значення: 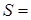
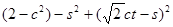
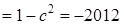 ,
,
при 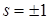 та
та 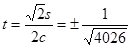 або
або 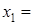
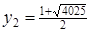 та
та 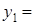
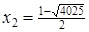 .
.
24.Нехай 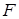 – множина всіх функцій
– множина всіх функцій 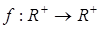 таких, що
таких, що 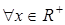
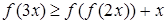 .
.
Знайдіть найбільше 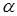 , таке, що для всіх
, таке, що для всіх 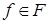
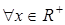 виконується умова:
виконується умова:
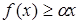 .
.
Відповідь: 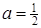 .
.
Розв’язання. Функція 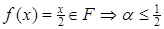 .
.
Нехай 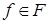 . Далі
. Далі 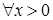 з умови маємо, що
з умови маємо, що 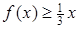 .
.
Розглянемо послідовність 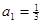 ,
, 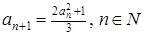 . З умови за індукцією легко бачимо, що
. З умови за індукцією легко бачимо, що 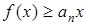 . Також за індукцією маємо, що
. Також за індукцією маємо, що 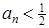 . Також
. Також 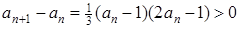 . Тому послідовність
. Тому послідовність 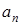 зростаюча та обмежена. А тому існує
зростаюча та обмежена. А тому існує 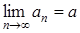 . Розв’язуючи рівняння
. Розв’язуючи рівняння 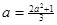 при умові
при умові 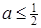 маємо, що
маємо, що 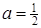 .
.
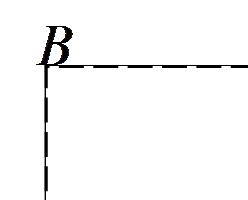 25. Від прямокутника
25. Від прямокутника 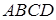 зі сторонами
зі сторонами 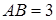 та
та 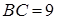 відрізали прямокутний трикутник
відрізали прямокутний трикутник 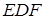 , де
, де 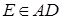 ,
, 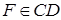 ,
, 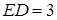 та
та 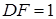 . Знайдіть максимальну площу прямокутника, сторони якого паралельні сторонам
. Знайдіть максимальну площу прямокутника, сторони якого паралельні сторонам 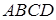 , який можна вирізати з п’ятикутника, що залишився.
, який можна вирізати з п’ятикутника, що залишився.
Відповідь: 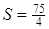 .
.
Розв’язання. Позначимо вершину шуканого прямокутника найбільшої площі, яка лежить на відрізку  , через
, через 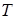 (рис. 13). Очевидно, що така вершина існує, інакше неважко збільшити площу вирізаного прямокутника. Нехай відстань від
(рис. 13). Очевидно, що така вершина існує, інакше неважко збільшити площу вирізаного прямокутника. Нехай відстань від 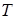 до сторін
до сторін 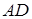 та
та 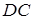 відповідно через
відповідно через 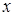 та
та 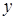 . Тоді шукана площа дорівнює
. Тоді шукана площа дорівнює 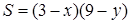 . З подібності запишемо, що
. З подібності запишемо, що 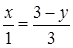 . Тому
. Тому 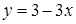 . Тоді
. Тоді 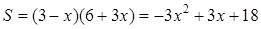 . Парабола гілками донизу, тому досягає максимуму в точці
. Парабола гілками донизу, тому досягає максимуму в точці 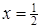 , що належить до припустимих значень
, що належить до припустимих значень 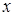 . При цьому максимальна площа дорівнює
. При цьому максимальна площа дорівнює 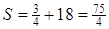 .
.
