Глава 4. Функции нескольких переменных

Определение функции нескольких переменных

При рассмотрении функций нескольких переменных ограничимся подробным описанием функций двух переменных, т.к. все полученные результаты будут справедливы для функций произвольного числа переменных.

Если каждой паре независимых друг от друга чисел (х, у) из некоторого множества по какому-либо правилу ставится в соответствие одно или несколько значений переменной z, то переменная z называется функцией двух переменных.Обозначение z = f(x, y)

Если паре чисел (х, у) соответствует одно значение z, то функция называется однозначной, а если более одного, то – многозначной.

Областью определения функции z называется совокупность пар (х, у), при которых функция z существует.

Окрестностью точки М₀(х₀, у₀) радиуса r называется совокупность всех точек (х, у), которые удовлетворяют условию .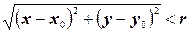

Число А называется пределом функции f(x, y) при стремлении точки М(х, у) к точке М₀(х₀, у₀), если для каждого числа e > 0 найдется такое число r >0, что для любой точки М(х, у), для которых верно условие 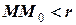, или условие .

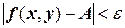Записывают: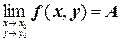

Частные производные

Пусть в некоторой области задана функция z = f(x, y). Возьмем произвольную точку М(х, у) и зададим приращение Dх к переменной х. Тогда величина D_xz = f(x + Dx, y) – f(x, y) называется частным приращением функции по х.

Можно записать .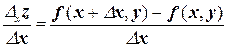

Тогда 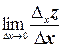называется частной производнойфункции z = f(x, y) по х. Обозначение: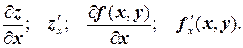

Аналогично определяется частная производная функции по у .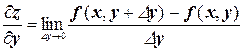

Полный дифференциал

Для функции f(x, y) выражение Dz = f(x + Dx, y + Dy) – f(x, y) называется полным приращением.

Выражение 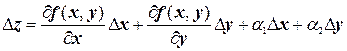называется полным приращениемфункции f(x, y) в некоторой точке (х, у), где a₁ и a₂ – бесконечно малые функции при Dх ® 0 и Dу ® 0 соответственно.

Полным дифференциаломфункции z = f(x, y) называется главная линейная относительно Dх и Dу часть приращения функции Dz в точке (х, у).

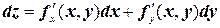
Для функции произвольного числа переменных:

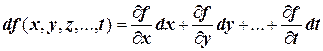
Примеры

№1. Найти частные производные функций:

а) ;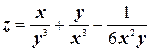

б) ;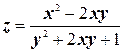

в) .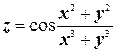

Решение.

а) Частные производные функции двух и более переменных определяются по тем же формулам и правилам, что и функции одной переменной. Следует помнить только одно правило: если по одной переменной дифференцируем, то остальные считаются постоянными.

Имеем: (напомним, что ):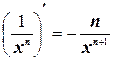

;

.

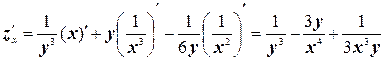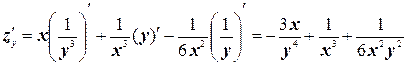б) Воспользуемся правилом дифференцирования дроби:

;

.

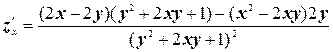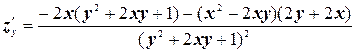в) Здесь имеем дело с производными сложной функции и дроби.

.

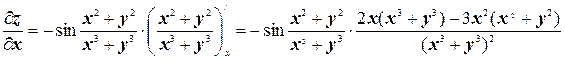Ввиду симметрии выражения 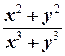относительно х и у можно записать сразу

.

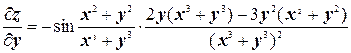№2. Найти полный дифференциал функций:

а) ;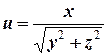

б) .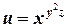

Решение.

а) Так как 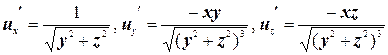, то полный дифференциал имеет вид .

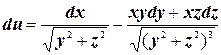б) Вычислим частные производные по х, у, z

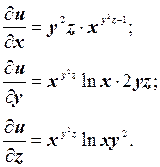
Таким образом, полный дифференциал

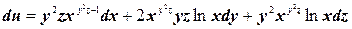
Варианты заданий

№4.1. Найти частные производные, частные дифференциалы данных функций по каждой из независимых переменных (x, y, z, t, …) и полный дифференциал:

а) ;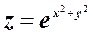

б) ;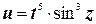

в) ;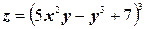

г) ;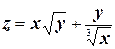

д) ;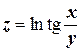

е) ;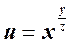

ж) ;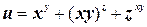

з) ;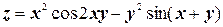

и) ;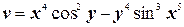

к) .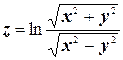

Контрольные вопросы