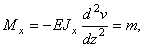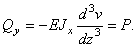Перемещения при изгибе балок

Дифференциальное уравнение изогнутой оси упру­гой балки

При расчете балок на изгиб инженер интересуется не только напряже­ниями, возникающими от действия внешних сил, но и перемещениями от действия тех же сил. Одно из требований к элементам конструкций, чтобы перемещение не превосходило некоторого допусти­мого значения, обусловленного требованиями эксплуатации. Это условие называется условием жесткости либо конструктивной прочности.

При расчете строительных и машиностроительных конструкций на жесткость(в большинстве случаев по прогибам, по углам поворота) должно соблюдаться условие

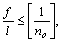
т.е. относительный прогиб f/l, подсчитанный при действии нормативных нагрузок, не должен превышать установленный нормами предельный прогиб 1/n_o для данного вида конструкции.

Для обеспечения нормальной работы подшипников скольжения и роликовых подшипников качения иногда ставится дополнительное условие жесткости – ограничение угла поворота 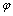опорных сечений:

.

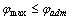Допускаемый угол поворота 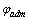берется из соответствующих справочников. В среднем 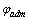составляет 0,001 рад.

Рассмотрим плоский чистый изгиб балки (рис. 6.41, а).

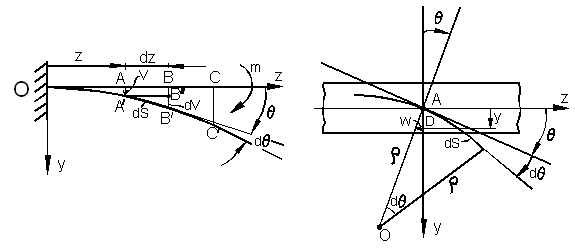
а) б)

Рис. 6.41

В результате действия изгибающего момента m ось балки ОС изгибается и занимает некоторое положение ОС'. Произвольная точка А оси балки, характе­ризуемая координатой 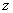, перемещается в новое положение А'. Перемещение, изображаемое направленным отрезком 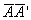, назовем прогибом балки для точки А с координатой 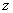и обозначим v. Проведем в точке А' касательную к изогнутой оси балки. Она образует с осью 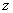угол .

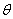Из рис. 6.41,б видно, что этот угол в силу взаимной перпендикулярности сто­рон в точности равен углу поворота поперечного сечения. При изменении 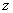, т.е. при переходе к другим точкам оси балки, прогиб v и угол поворота 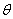поперечного сечения изменяется. Следовательно, они являются функциями :

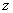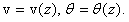(19)

Горизонтальное перемещение w произвольной точки D поперечного се­чения на расстоянии 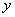от оси балки равно:

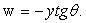(20)

Из треугольника А'В'В" следует, что первая производная от функции прогиба :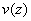

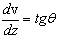(21)

равна тангенсу угла наклона касательной к изогнутой оси балки в точке А с координатой 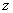. Из этого же треугольника получаем

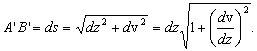(22)

Из рис. 6.41,б находим 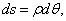где 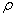- радиус кривизны дуги 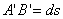. Следовательно, кривизна изогнутой оси в точке А равна:

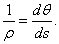(23)

Дифференцируя (21) по 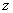и учитывая (19), (22), (23), получаем:

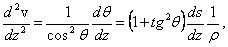
откуда

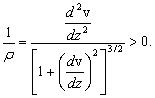(24)

Формула для кривизны балки

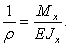
для положительных значений 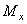. В нашем примере на рис. 6.41 изгибающий момент 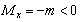. Поэтому эту формулу мы должны использовать в виде:

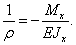(25)

Приравнивая (24), (25), получаем точное дифференциальное уравнение изогнутой оси балки:

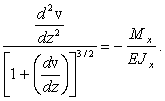(26)

Если прогибы 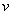балки малы по сравнению с ее линейными размерами, то и углы поворота сечений 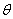- малые величины и, согласно (21)-(24), можно считать:

, ,

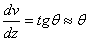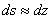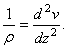
Тогда дифференциальное уравнение (26) упрощается и принимает вид

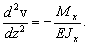(27)

Уравнение (27) носит название приближенного дифференциального уравнения изогнутой оси упругой балки. Оно получено для случая чи­стого изгиба, но может быть использовано и при поперечном, когда мо­мент 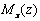является функцией .

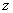Интегрируя (27), получаем:

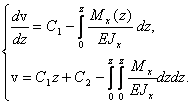(28)

Произвольные постоянные C₁, С₂ в (28) имеют простой геометрический смысл. Обозначим через 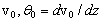прогиб и угол поворота cечения соответственно в начале координат при 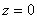. Тогда при 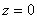из (10) получаем:

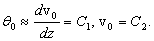
Величины 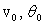называют начальными параметрами задачи по определению перемещений в балках.

Соотношения (28) запишем в виде

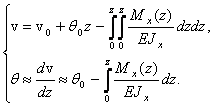(29)

Так как

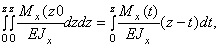
то решение (29) можно записать в виде:

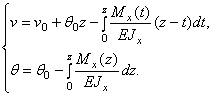
В соответствии с дифференциальными зависимостями Журавского

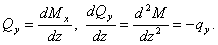(30)

Дифференцируя (27) дважды по 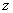и используя зависимости (30), находим

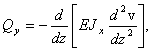(31)

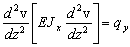. (32)

При постоянной жесткости 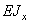получаем

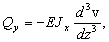(33)

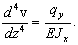(34)

Уравнения (32), (34) представляют собой вторую форму дифферен­циальных уравнений изогнутой оси балки четвертого порядка.

Общее решение неоднородного уравнения (34) имеет вид

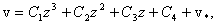(35)

где 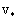- его частное решение. Постоянные 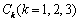находятся из условий на опорах балки. Эти условия называют граничными или краевыми.

Рассмотрим типичные условия закрепления или опирания балок (рис. 6.42). Изогнутая ось балки изображена тонкой линией.

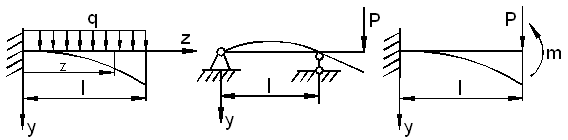
а) б) в)

Рис. 6.42

а) Край балки жестко защемлен (рис. 6.42,а). При z = 0 на защемленном крае прогиб и угол поворота сечения равны нулю, т.е.

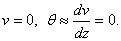
б) Край балки свободен от закрепления и нагрузки (рис.6.42,а). В этом случае при 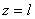равны нулю: момент и перерезывающая сила:

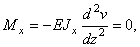
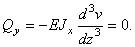
в) Край балки шарнирно закреплен либо свободно опёрт (рис. 6.42,б). При z = 0 край балки шарнирно закреплен. Здесь прогиб 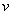и момент 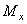равны нулю, т.е.

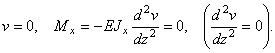
При 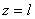балка свободно лежит на опоре. Прогиб равен нулю, но изгибающий момент в сечении балки отличен от нуля. Поэтому здесь только одно граничное условие .

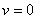г) Незакрепленный край балки с действующими сосредоточенными силой и моментом (рис. 6.42,в).

В этом случае при 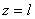имеем статические граничные условия: