Решение задания в Excel
Формулы, использованные в Excel:
для х1: =($E$6-$B$6*B11-$C$6*C11)/$A$6;
для х2: =($E$7-$A$7*A12-$C$7*C11)/$B$7;
для х1: =($E$8-$A$8*A12-$B$8*B12)/$C$8;
для нахождения максимума среди разностей:
=МАКС(ABS(A12-A11);ABS(B12-B11);ABS(C12-C11));
для определения приближенности к заданному значению:
=ЕСЛИ(D12<$D$10;"Стоп";"Продолжать").
Выполнение задания в Excel:
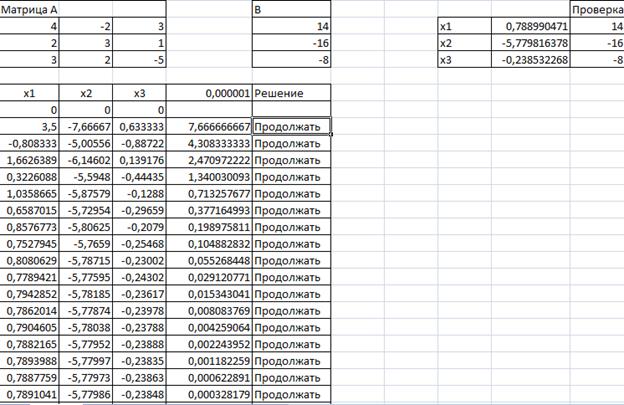
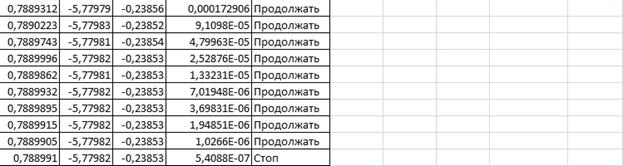
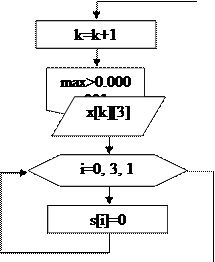
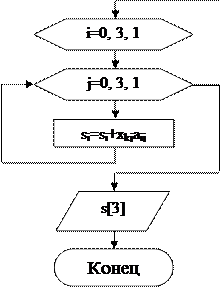
Алгоритм решения задачи:
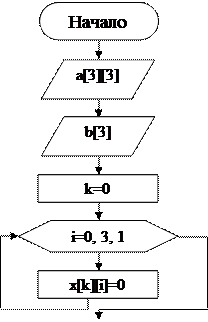 |

|
 |
 | ||||
 | ||||
 |
Текст программы в Си:
#include <stdio.h>
#include <conio.h>
#include <math.h>
int main()
{int a[3][3]={{4,-2,3},{2,3,1},{3,2,-5}}, i,j; float max;
int b[3]={14,-16,-8};
printf("massiv a[3][3]:");
for (i=0; i<3; i++)
{
printf("\n\n");
for (j=0; j<3; j++)
printf ("%d ", a[i][j]);
}
printf("\n\n\n");
printf("massiv b[3]:");
printf("\n\n");
for (i=0; i<3; i++)
printf("%d ", b[i]);
int k=0;
float x[42][3];
for (i=0; i<3; i++)
x[k][i]=0;
do {
x[k+1][0]=(b[0]-a[0][1]*x[k][1]-a[0][2]*x[k][2])/a[0][0];
x[k+1][1]=(b[1]-a[1][0]*x[k+1][0]-a[1][2]*x[k][2])/a[1][1];
x[k+1][2]=(b[2]-a[2][0]*x[k+1][0]-a[2][1]*x[k+1][1])/a[2][2];
float d[3];
for (i=0; i<3; i++)
d[i]=fabs(x[k+1][i]-x[k][i]);
for (i=0; i<3; i++)
{
max=d[0];
if (d[i+1]>max)
max=d[i+1];}
k++;
} while (max>0.000001);
printf("\n\n\n");
printf("vector resheniya X[3]:");
printf("\n\n");
for (i=0; i<3; i++)
printf("%f ", x[k][i]);
float s[3];
for (i=0; i<3; i++)
s[i]=0;
for (i=0; i<3; i++)
{
for(j=0; j<3; j++)
s[i]=s[i]+x[k][j]*a[i][j];
}
printf("\n\n\n");
printf("Proverka:");
printf("\n\n");
for (i=0; i<3; i++)
printf("%.0f ", s[i]);
getch();
}
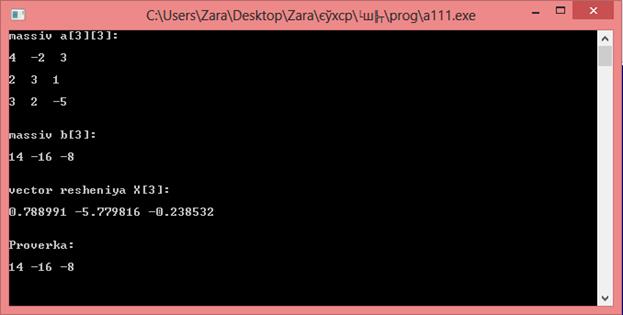
Результат выполнения программы:
Заключение
В данной расчетно-графической работе я изучила метод Зейделя, который относится к методам простой итерации. При решении задачи в Excel я использовала математические функции МАКС, ABS, и логическую функцию ЕСЛИ.
При решении задачи в Си, я использовала два вида циклических операторов: оператор с постусловием и с параметрами. Оператор с постусловием я использовала, так как мне было неизвестно число повторов цикла, и он продолжался до тех пор, пока значение не приблизилось к заданному мной (т.е. 0,000001). А при проверке результата, т.е. при получении исходного массива b[3] при помощи вектора решения я использовала циклический оператор с параметрами for, так как число повторов известно, а значит он является более удобным.
Список использованной литературы
1. КерниганБ., РитчиД.ЯзыкпрограммированияСи = TheCprogramminglanguage. — 2-еизд. — М.: Вильямс, 2007. — С. 304.
2. Герберт ШилдтC: полное руководство, классическое издание = C: TheCompleteReference, 4thEdition. — М.: «Вильямс», 2010. — С. 704.
3. Прата С. Язык программирования С: Лекции и упражнения = C Primer Plus. — 1-е изд. — М.: Вильямс, 2006. — С. 960.
4. Кочан С. Программирование на языке Си = Programming in C. — 3-е изд. — М.: Вильямс, 2006. — С. 496.
5. Гукин Д. Язык программирования Си для «чайников» = C For Dummies. — М.: Диалектика, 2006. — С. 352.
6. http://vplaksina.narod.ru/uchebnik/algoritm.htm
