Вершинная и реберная связность

Вершинной связностью графа Gназывается наименьшее число вершин, удаление которых приводит к несвязному, или тривиальному, графу; обозначается: c(G).

c( 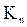)=n-1; c( 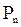)=1; c( 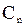)=2.

Реберной связностью графа G называется наименьшее число ребер, удаление которых приводит к несвязному графу; обозначается: .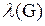

l( 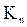)=n-1; l( 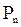)=1; l( 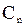)=2.

Для тривиального графа реберную связность полагают равной 0.

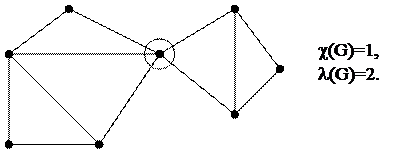Пример:

Вершина v графа G называется точкой сочленения,илиразделяющей вершиной, если граф G\{v} имеет больше компонент связности, чем граф G.

Ребро е графа G называется мостом, если его удаление приводит к нарушению связности графа.

Пример:

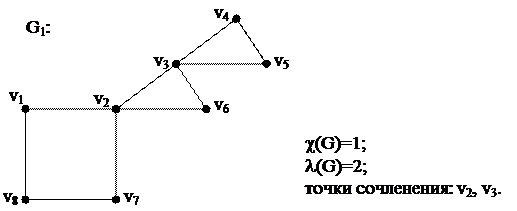Связный непустой граф называется неразделимым, если в нем отсутствуют точки сочленения.

Блок – это максимальный неразделимый подграф исходного графа.

Теорема Уитни.Пусть 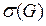- минимальная степень вершин графа G, тогда справедливо следующее неравенство: c(G) .

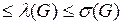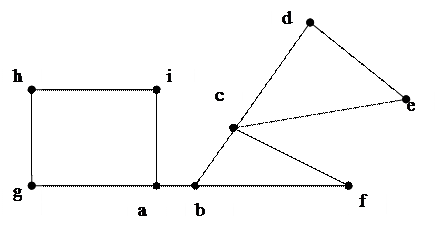Пример:

Граф не является неразделимым;

блоки графа:{c,d,e},{c,b,f},{a,g,h,i},{a,b}.

КРАТЧАЙШИЕ МАРШРУТЫ В ГРАФАХ

Пусть задан граф G=(V,E),ребрам которого приписаны веса (стоимости), задаваемые матрицей 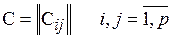. Задача состоит в нахождении кратчайшего пути от заданной начальной вершины sÎV до заданной конечной вершины tÎV при условии, что такой путь существует. Элементы матрицы весов могут быть положительными, отрицательными или нулевыми. Единственное ограничение состоит в том, чтобы граф не содержал циклов с суммарным отрицательным весом.

Задачи данного типа имеют следующие модификации:

- для заданной начальной вершины sнайти кратчайшие пути от нее ко всем другим вершинам графа;

- найти кратчайшие пути между всеми парами вершин графа.

АЛГОРИТМ ДЕЙКСТРЫ

Постановка задачи. Имеется произвольный взвешенный (n,m)-граф (в матрице весов нет отрицательных чисел), т.е.:

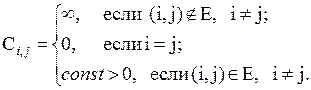
Требуется найти кратчайший маршрут от вершины s ко всем остальным вершинам графа.

Алгоритм основан на приписывании вершинам временных пометок, причем пометка вершины дает верхнюю границу длины пути от s к данной вершине. Эти пометки постепенно уменьшаются с помощью итерационной процедуры, и на каждом шаге итерации одна из временных пометок становится постоянной. Последнее указывает на то, что пометка уже не является верхней границей, а дает точную длину кратчайшего пути от s к рассматриваемой вершине.

Алгоритм.

Пусть l(x_i) – пометка вершины x_i, Г(р) – множество вершин графа, смежных с вершиной р.

Шаг 1.Присвоение начальных значений.

Положить l(s)=0 и считать эту пометку постоянной. Положить l(x_i)=¥ для всех x_i ≠s и считать эти пометки временными. Положить p=s.

Шаг 2.Обновление пометок.

Для всех x_i ÎГ(р), пометки которых временные, заменить пометки в соответствии со следующим выражением:

l(x_i)=min[l(x_i),l(p)+c(p,x_i)] . (1)

Шаг 3.Превращение пометки в постоянную.

Среди всех вершин с временными пометками найти такую, для которой

l(x_i^*)=min[l(x_i)].

Шаг 4. Считать пометку вершины x_i^* постоянной; положить р= x_i^*.

Шаг 5. Если р=t, то l(p) является длиной кратчайшего пути. Останов.

Если р¹t, то перейти к шагу 2.

Замечание. Как только длины кратчайших путей будут найдены, сами пути можно получить при помощи рекурсивной процедуры с использованием соотношения

L(x_i’)+c(x_i’, x_i)=L( x_i);

т.к. вершина x_i’непосредственно предшествует вершине x_iв кратчайшем пути от s к x_i, то для любой вершины x_iсоответствующую вершину x_i’можно найти как одну из оставшихся вершин.

Пример:

Матрица весов для графа G:

		∞		∞
	∞		∞		∞
		∞
	∞					∞	∞
		∞
				∞
				∞

Найти кратчайшие расстояния от 1 вершины ко всем остальным.

1) l(1) = 0;

l(2) = l(3) = … = l(7) =∞;

p = 1.

2) Г(1) = {3,5,6,7};

l(3) = min(l(3), l(1)+C(1,3)) = min(∞,0+4)=4;

l(5) = min(l(5), l(1)+C(1,5)) = 16;

l(6) = min(l(2), l(1)+C(1,2)) = 14;

l(7) = min(l(2), l(1)+C(1,2)) = 2.

3) min(4,16,14,2) = 2;

min = l(7) = 2;

p = 7.

4) Г(7) ={1,2,3,5,6};

l(2) = min(l(2), l(7)+C(2,7)) = min(∞, 2+9)=11;

l(3) = min(l(3), l(7)+C(3,7)) = 4;

l(5) = min(l(5), l(7)+C(5,7)) =16;

l(6) = min(l(6), l(7)+C(6,7)) = 14.

5) min(11,4,16,14) = 4;

min = l(3) = 4;

p = 3.

6) Г(3) = {1,4,5,6,7};

l(4) = min(l(4), l(3)+C(4,3)) = 13;

l(5) = min(l(5), l(3)+C(5,3)) = 16;

l(6) = min(l(6), l(3)+C(6,3)) = 14.

7) min(13,16, 14) = 13;

min = l(4) = 13;

p=4.

8) Г(4) = {2,3,5};

l(5) = min(l(5), l(4)+C(5,4)) = 16;

l(2) = min(l(6), l(3)+C(6,3)) = 11.

9) min(11,16) = 11;

min = l(2) =11;

p = 2.

10) Г(2) = {4,6,7};

l(6) = min(l(6), l(2)+C(2,6)) = 14.

11) min = l(6) =14;

p = 6.

12) l(5) = min(l(5), l(6)+C(5,6)) = 16;

p=5.

Таким образом, найдены следующие кратчайшие маршруты от вершины 1:

(1-2): (1,7,2)=11;

(1-3): (1,3)=4;

(1-4): (1,3,4)=(1,7,3,4)=(1,7,2,4)=13;

(1-5): (1,5)=16;

(1-6): (1,6)=14;

(1-7): (1,7)=2.

АЛГОРИТМ ФОРДА

Алгоритм Форда – обобщение алгоритма Дейкстры для случая, когда некоторые ребра имеют отрицательные веса.

На шаге 2 алгоритма пересчет l(x) с помощью соотношения (1) производится для любых вершин, а не только для непомеченных. Значения l(x) могут уменьшаться как для помеченных, так и для непомеченных вершин, т.к. существуют ребра с отрицательным весом.

Если для некоторой помеченной вершины х происходит уменьшение величины l(x), то с этой вершины пометка снимается.

Процедура заканчивается, когда все вершины помечены, и после выполнения шага 2 ни одна из величин l(x) не изменяется.

Алгоритм.

Пусть l^k(x_i) – пометка вершины х_i в конце (k+1)-й итерации, Г(s) – множество вершин, смежных с вершиной s.

Шаг 1.Присвоение начальных значений.

Положить S= Г(s), k=1, l¹(s)=0, l¹(x_i)=c(s, x_i) для всех x_iÎ Г(s). Положить l¹(x_i)=¥ для всех остальных x_i.

Шаг 2.Обновление пометок.

Для каждой вершины x_i Î Г(s) (x_i¹s) изменить ее пометку следующим образом:

l^k+1(x_i)=min[l^k(x_i),min{ l^k(x_i)+c(x_j, x_i)}] для x_jÎ T_i, где T_i=Г(x_i)ÇS.

Шаг 3.Проверка на окончание.

Если k£n-1 и l^k+1(x_i)= l^k(x_i) для всех x_i, то пометки равны длинам кратчайших путей. Останов.

Если k<n-1 и l^k+1(x_i)¹ l^k(x_i) для некоторой вершины x_i, то перейти к шагу 4.

Если k=n-1 и l^k+1(x_i)¹ l^k(x_i) для некоторой вершины x_i, то в графе существует цикл отрицательного веса и задача не имеет решения. Останов.

Шаг 4.Подготовка к следующей итерации.

Обновить множество следующим образом:

S={x_i | l^k+1(x_i) ¹ l^k(x_i)}.

Шаг 5. Положить k=k+1 и перейти к шагу 2.

Замечание. Алгоритм Форда не решает задачу при наличии цикла отрицательной длины. Для его обнаружения в процессе работы алгоритма просчитывается, сколько раз помечается каждая вершина: если вершина помечается ровно n раз, где n – число вершин графа, - процедура заканчивает работу: существует цикл отрицательной длины.

Пример:

Матрица весов для графа G:

		∞		∞
	∞		∞		∞
		∞
	∞					∞	∞
		∞
				∞
				∞

1) s=1; вершины, смежные вершине 1: S= Г(s)={3,5,6,7},

k=1; l¹(1)=0,

l¹(3)=4, l¹(5)=16, l¹(6)=14, l¹(7)=2, l¹(2)= l¹(4)=¥;

2) Г(s)={2,3,4,5,6,7} - вершины, смежные вершинам 3,5,6,7;

для 2: Т₂={7,6,4}Ç{3,5,6,7}={7,6}, где {7,6,4} - вершины, смежные вершине 2;

l²(2)=min(¥, min(2+9,14+3))=11;

для 3: Т₃={1,4,5,6,7}Ç{3,5,6,7}={5,6,7}, где {1,4,5,6,7} - вершины, смежные вершине 3;

l²(3)=min(4, min(16+12,14+10,2+2))=4;

для 4: Т₄={2,3,5}Ç{3,5,6,7}={3,5}, где {2,3,5} - вершины, смежные вершине 4;

l²(4)=13;

для 5: Т₅={1,3,4,6,7}Ç{3,5,6,7}={3,6,7}, где {1,3,4,6,7} - вершины, смежные вершине 5;

l²(5)= 16;

для 6: Т₂={1,2,3,5,7}Ç{3,5,6,7}={3,5,7}, где {1,2,3,5,7} - вершины, смежные вершине 6;

l²(6)= 14;

для 7: Т₂={1,2,3,5,6}Ç{3,5,6,7}={3,5,6}, где {1,2,3,5,6} - вершины, смежные вершине 7;

l²(7)=2;

3) переходим к шагу 4, обновляем множество S;

4) S={2,4};

5) k=2; переходим к шагу 2;

6) Г(S)={2,3,4,5,6,7} - вершины, смежные вершинам 2,4;

для 2: Т₂={7,6,4}Ç{2,4}={4};

l³(2)=min(11, 13+2))=11;

для 3: Т₃={1,4,5,6,7}Ç{2,4}={4};

l³(3)=min(4, 13+9)=4;

для 4: Т₄={2,3,5}Ç{2,4}={2};

l³(4)= min(13, 11+2)=13;

для 5: Т₅={1,3,4,6,7}Ç{2,4}={4};

l³(5)= 16;

для 6: Т₂={1,2,3,5,7}Ç{2,4}={2};

l³(6)= 14;

для 7: Т₂={1,2,3,5,6}Ç{2,4}={2}

l³(7)=2.

7) k£n-1 и l^k+1(x_i)= l^k(x_i) для всех x_i, следовательно, пометки равны длинам кратчайших путей.

Кратчайшие маршруты от вершины 1:

(1-2):(1,7,2)=11;

(1-3): (1,3)=4;

(1-4): (1,3,4)=(1,7,3,4)=(1,7,2,4)=13;

(1-5): (1,5)=16;

(1-6): (1,6)=14;

(1-7): (1,7)=2.

АЛГОРИТМ ФлойДА

Алгоритм базируется на использовании последовательности из n преобразований (итераций) начальной матрицы весов. При этом на k-той итерации матрица представляет длины кратчайших путей между каждой парой вершин с тем ограничением, что путь между x_i и x_j (для любых x_i и x_j) содержит в качестве промежуточных только вершины из множества { x₁ , x₂ ,…, x_n}.

Все циклы в графе G имеют неотрицательный суммарный вес.

Алгоритм.

Шаг 1.Присвоение начальных значений.

Положить k=0.

Шаг 2.

k=k+1.

Шаг 3.

Для всех i ¹ k таких что c_ik¹¥, и для всех j ¹k таких что c_kj ¹¥ введем операцию:

c_ij=min[c_ij, (c_ik+c_kj)]. (2)

Шаг 4.Проверка на окончание.

Если c_ij <0, то в графе существует цикл отрицательного веса, содержащий вершину x_i; решения нет. Останов.

Если все c_ij ³ 0 и k=n, то получено решение и матрица дает длины всех кратчайших путей. Останов.

Если все c_ij ³ 0, но k<n, то вернуться к шагу 2.

Пример:

Пусть задан граф G следующего вида:

Матрица весов: Матрица путей:

k=0;

k=1;

		∞		∞
	∞		∞		∞
		∞
	∞					∞	∞
		∞
				∞
				∞

k=2;

		∞		∞
	∞		∞		∞
		∞
	∞
		∞

k=3;

		∞
	∞		∞		∞
		∞
		∞

k=4;

k=5;

k=6;

k=7;

Матрица q=[q_ij] – матрица, в которой элемент q_ij указывает вершину, непосредственно предшествующую вершине х_j в кратчайшем пути от х_i к х_j. Матрице q присваиваются начальные значения q_ij= х_i для всех х_i и х_j. На шаге 3 алгоритма обновление матрицы происходит следующим образом:

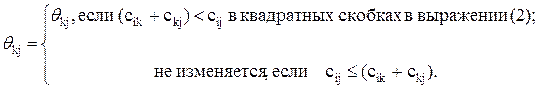
В конце алгоритма кратчайшие пути получаются непосредственно из заключительной матрицы q.

Таким образом, матрица всех кратчайших маршрутов:

Матрица путей:

		1,7,2	1,3	1,3,4	1,5	1,6	1,7
	2,7,1		2,4,3	2,4	2,4,5	2,6	2,7
	3,1	3,4,2		3,4	3,5	3,6	3,7
	4,3,1	4,2	4,3		4,5	4,2,6	4,2,7
	5,1	5,4,2	5,3	5,4		5,6	5,7
	6,1	6,2	6,3	6,2,4	6,5		6,7
	7,1	7,2	7,3	7,2,4	7,5	7,6

Кратчайшие маршруты от вершины 1:

(1-2): (1,7,2)=11;

(1-3): (1,3)=4;

(1-4): (1,3,4)=(1,7,3,4)=(1,7,2,4)=13;

(1-5): (1,5)=16;

(1-6): (1,6)=14;

(1-7): (1,7)=2.

Контрольные вопросы

1. Определение маршрута, цепи, цикла.

2. Какой граф называется связным? Что такое компонента связности?

3. Привести примеры графов, которые имеют все периферийные и все центральные вершины.

4. Что такое эксцентриситет?

5. Чем диаметр графа отличается от его радиуса (дайте их определение)?

6. Что такое число вершинной и реберной связности?

7. Дайте определения моста и точки сочленения.

8. Для произвольного графа постройте матрицу расстояний (вес любого ребра равен 1).

9. Привести пример графа, удовлетворяющего строгому неравенству теоремы Уитни.

10. Сформулируйте задачу нахождения кратчайших маршрутов в графе.

ДЕРЕВЬЯ И ОСТОВЫ