Дифференциалдық теңдеулерді шешу және әдістері. Коши есебі. Эйлер әдістері

Физикадағы ең маңызды және көп тараған есептердің бірі әртүрлі қозғалыс теңдеулері. Олардың қарапайымдары алғашқы шартпен берілген бір немесе бірнеше диффренциалдық теңдеулерді шешуді қажет етеді. Бірақ көп жағдайда бұндай теңдеулерді аналитикалық шешу мүмкін болмайды, сондықтан Коши есебін шешуге негізделген сандық әдістерді қолданнамыз. Сонымен қатар бұл әдістердің көмегімен шамалары уақытқа байланысты өзгеретін динамикалық есептерді шешуге болады.

Эйлер әдісі. Осындай айрымдық әдістің бірі Эйлер әдісі болып табылады. Мысал ретінде (14.2) алғашқы шартпен бірінші ретті диффренциалдық теңдеуді (14.1) шешуді қарастырамыз:

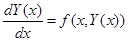(14.1)

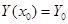(14.2)

Бұл есептің шешімі айырымдық әдіс бойынша тордық функция түрінде, яғни кесте түрінде 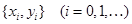ізделінеді, мұндағы 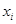- 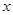тәуелсіз айнымалысының көптік мәндері (олар түйін деп аталады ), 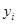- түйіндегі 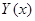-тің дәл шешімін аппроксимациялайтын мән. Түйіндерді тең қатарлы орналасқан деп есептесек, яғни 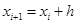, 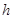-қадам деп аталады, ол тұрақты шама болып табылады. Енді (14.1), (14.2) есебі тордық функцияны анықтайтын есепке келеді:

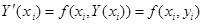(14.3)

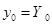(14.4)

(14.3) туындысын шеткі-айырымдық өрнекпен алмастырамыз:

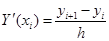(14.5)

Осыған байланысты 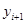үшін келесі есептеу формуласын аламыз:

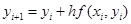. (14.6)

Дәлірек Эйлер әдісі.Әдісті қарастыру үшін 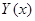функциясын Тейлор қатарына жіктейміз:

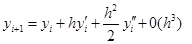(14.7)

Енді екінші ретті туындыны шеткі-айырымдық әдіс бойынша жазамыз:

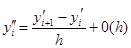. (14.8)

(14.8)-ші өрнекті (14.7)-ге қоя отырып келесі өрнекті аламыз:

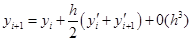. (14.9 )

Туындыларды келесі өрнектермен алмастырамыз

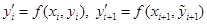. (14.10)

Мұндағы 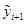-(14.6) формула бойынша анықталады.

Бұл әдістерден басқа диффренциалдық теңдеуді шешетін Рунге-Кутта әдісі бар.

6. Диффренциалдық теңдеулер жүйесін шешу. Рунге-Кутта әдісі.

Алғашқы шартпен берілген диффренциалдық теңдеулерді шешу үшін Эйлер әдістерінен басқа да бір қадамды әдістер бар. Мысал ретінде екі теңдеуден тұратын диффренциалды теңдеулер жүйесін қарастырамыз:

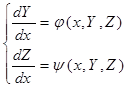(14.11)

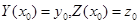
Рунге-Кутта әдісі Эйлер әдістеріне қарағанда дәлірек әдіс болып саналады. Есептеу үлгісі келесі түрде болады:

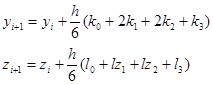(14.12)

мұндағы

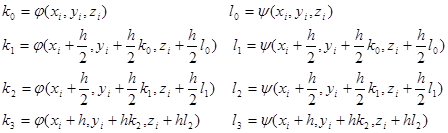
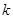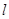Егер жүйе бірнеше теңдеуден тұрса, онда мен сияқты сонша коэффиценттер қажет. Айта кететін жағдай, жоғарғы ретті диффренциалдық теңдеулер үшін Коши есебін бірінші ретті дифференциалдық теңдеулер жүйесін шешуге келтіруге болады.

7.10. Дербес туындылы теңдеулерді шешу әдістері. Лаплас теңдеуі

Жылуөткізгіштік теңдеуді үшін аралас есепті қарастырамыз.

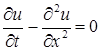(15.8)

теңдеуін және қанағаттандыратын 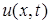функциясын табу керек.

Бастапқы шарт

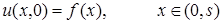, (15.9)

және шекаралық шарттар

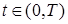, . (15.10)

берілген.

Есепті шешу үшін тор әдісін қолданамыз. Әдістің негізінетуындының н әндерін шекті-айырымды қатынаспен алмастыру жатыр. Тәуелсіз екі айнымалы бар жағдайды қарастырамыз. А йталық хОу жазықтығында 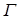шекарасымен қандай да бір 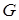облысы берілсін (Сурет 1).

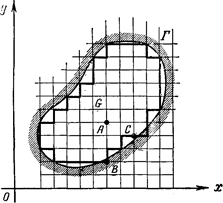
Сурет 1

Жазықтықта екі паралель түзулер жиынтығын қарастырамыз:

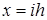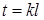, , i=0,1,2,…, k=0,1,2,…

Осы түзулердің қиылысқан нүктелерін түйіндер деп атайды.

Іздеп отырған и=и(х,у) функцияның мәндері тор түйіндерінде 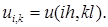деп белгілейік. Әр ішкі түйіндердегі дербес туындыны шекті айырым қатынастары арқылы алмастырамыз:

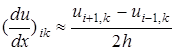
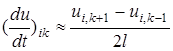
Шекаралық нүктелерде келесі түрдегі формуланы қолданамыз

, .

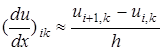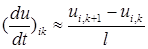Екінші ретті дербес туынды да сәйкесінше алмастырылады

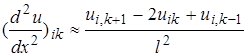
Енді 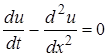түріндегі теңдеуден келесі теңдеуге көшеміз

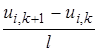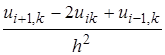- =0.

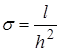деп алып, ішкі түйіндер үшін есептеуге арналған теңдеуді аламыз

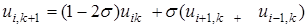(15.11)

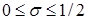болғанда (15.11) теңдеулері орнықты болады. 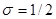болған кезде (15.9) теңдеуі мына түрде жазылады

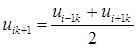(15.12)

Айталық 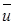(x,t) – (15.8)-(15.10) есептің шешімі болсын, 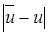– дәл мәннің тор әдісімен есептелген мәннен ауытқуы. Онда есептеу қателігі келесі формуламен есептелу керек

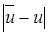
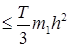, (15.13)

мұндағы = ,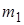

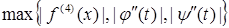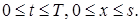
8. Интерполяция және оның түрлері. квадраттық интерполяциялар.

1. Интерполяция және оның түрлері.

Сызықты интерполяция. Сызықты интерполяцияда берілген нүктелерді қисық сызықтар арқылы қосамыз. Бұл жергілікті интерполяцияға жатады, себебі берілген нүктеге көршілес жатқан екі нүктені қарастырамыз.

Белгісіз функцияның мәні келесі түрде ізделінеді

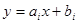. (12.1)

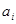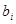және коэффиценттерін табу үшін, 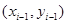және 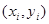нүктелері арқылы өтетін түзудің канондық теңдеуін жазамыз

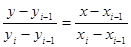. (12.2)

Бұл жерден

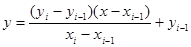. (12.3)

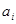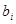Сосын (12.1) және (12.3) өрнектерін салыстыра отырып және коэффиценттерін табамыз

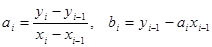. (12.4)

Квадраттық интерполяция.Квадраттық интерполяцияда функцияның мәнің келесі түрде ізделінеді

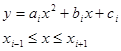(12.5)

Бұл жердегі белгісіз 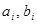және 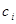коэффициенттерін табу үшін, үш нүкте 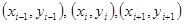арқылы өтетін параболла үшін теңдеулер жүйесін жазамыз