Собственные числа и собственные векторы самосопряженного оператора

Порядок выполнения работы:

Часть 1
1. Найти собственные числа и собственные векторы линейного оператора А.
2. Полученные собственные векторы проверить на ортогональность, а также согласно определению собственного числа и собственного вектора.
3. Провести преобразование матрицы линейного оператора к базису из собственных векторов.

Часть 2
1. Составить матрицу квадратичной формы, найти ее собственные числа и собственные векторы.
2. Полученные собственные векторы проверить на ортогональность, а также согласно определению собственного значения и собственного вектора.
3. Преобразовать заданное уравнение, перейдя в базис из ортонормированных собственных векторов, привести уравнение к каноническому виду.
4. Сделать чертеж исходной системы координат, новой системы координат и построить кривую второго порядка.

Литература

1. Высшая математика. Раздел: Линейная алгебра и аналитическая геометрия. Учебное пособие по выполнению типовых расчетов. - М., МИСиС, 1990, № 687, стр. 69-87.

Собственные значения и собственные векторы самосопряженного оператора. Приведение уравнения второго порядка к каноническому виду

Цель работы

1. Найти собственные значения и собственные векторы линейного оператора, имеющего симметрическую матрицу. Преобразовать матрицу линейного оператора к ортогональному базису из собственных векторов.
2. Привести уравнение кривой второго порядка к каноническому виду, изобразить эту кривую на плоскости.

Теоретическое введение

1. Линейные операторы, их собственные значения и собственные векторы.
В линейном пространстве L задан оператор А, если каждому вектору 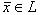по некоторому правилу поставлен в соответствие вектор .
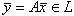Оператор A называется линейным, если для любых векторов пространства, и для любого действительного числа λ выполняются равенства:
, .
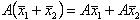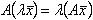Рассмотрим линейный оператор A в трехмерном линейном пространстве. Выберем в этом пространстве некоторый базис 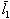, , 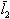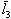. Оператор A приводит в соответствие каждому вектору x с координатами x₁, x₂, x₃ в выбранном базисе вектор 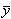, координаты которого в том же базисе вычисляются по формулам:

­ ­ ­

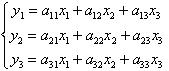(9.1)

или в матричной записи 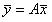, где A – матрица линейного оператора в базисе , , :

­ ­ ­

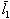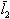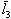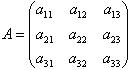(9.2)

Столбцы этой матрицы являются координатами векторов, которые оператор A ставит в соответствие базисным векторам , , :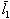

­ ­ ­ ­ ­ ­

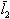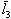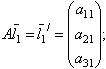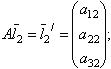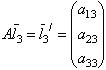(9.3)

Ненулевой вектор 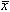называется собственным вектором линейного оператора A, если найдется такое число λ, что выполняется равенство: 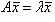. Само число λ называется собственным значением линейного оператораA, соответствующим вектору 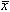. Собственные значения линейного оператора с матрицей (9.2) являются корнями характеристического уравнения, которое можно записать в виде |A – λE| = 0 или

­ ­ ­

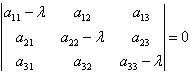(9.4)

Собственным вектором, соответствующим собственному значения λ является любой вектор 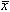= (x₁, x₂, x₃), координаты которого удовлетворяют системе линейных однородных уравнений:

­ ­ ­

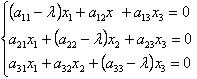(9.5)

Собственные векторы определяются условием (9.3) с точностью до числового множителя, поэтому решая систему (9.5), можно одну из ненулевых координат вектора 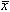принять равной любому конкретному значению.
Самосопряженный линейных оператор в любом ортонормированном базисе имеет симметрическую матрицу, т.е. матрицу A, совпадающую со своей транспонированной (A = A^T). Все его собственные значения – вещественны; собственные векторы такого линейного оператора, соответствующие различным собственным значениям, ортогональны, т.е. их скалярные произведения равны нулю. Последний факт можно использовать для контроля при нахождении собственных векторов.
Пусть координаты векторов линейного пространства и матрица линейного оператора рассматриваются относительно фиксированного базиса 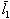, , 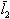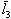. Допустим, что имеется другой – новый базис 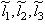. Если линейному оператору в исходном базисе 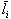соответствует матрица A, а в новом базисе 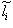– матрица 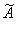, то между этими матрицами существует связь

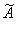= T -1AT­ ­ ­

(9.6)

где T – матрица перехода из исходного базиса в новый. Чтобы построить матрицу перехода T, надо координаты новых базисных векторов в исходной системе координат записать в столбцы матрицы T.
В случае, когда характеристическое уравнение имеет простые корни λ₁, λ₂, λ₃ соответствующие им собственные векторы

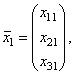
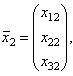
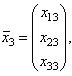
в свою очередь, образуют базис.
Матрица перехода T из исходного базиса в базис из собственных векторов записывается в виде:

­ ­ ­

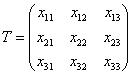(9.7)

матрица линейного оператора A в базисе из собственных векторов будет диагональная, причем на диагонали будут стоять соответствующие собственные числа:

­ ­ ­

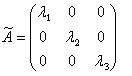(9.8)

2. Исследование полного уравнения кривой второго порядка.
Пусть уравнение кривой второго порядка в некоторой декартовой системе координат задано в виде:

a11x2 + 2a12xy + a22 y2 + 2a1x + 2a2 y + a = 0 ­ ­ ­

(9.9)

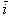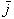Обозначим, как обычно, через и единичные векторы, направленные по осям декартовой системы координат. Группу старших членов уравнения (9.9) a₁₁x² + 2a₁₂xy + a₂₂ y² можно рассматривать как квадратичную форму от координат x, y вектора (x, y). Эта квадратичная форма связана с симметрической матрицей

­ ­ ­

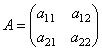(9.10)

Обозначим ортонормированный базис из ее собственных векторов ē₁ и ē₂, а соответствующие им собственные значения – λ₁ и λ₂. В указанном базисе квадратичная форма a₁₁x² + 2a₁₂xy + a₂₂ y² приводится к каноническому виду:

­ ­ ­

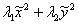(9.11)

Собственные числа λ₁ и λ₂ можно найти из характеристического уравнения

|A – λE| = 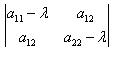= 0­ ­ ­

(9.12)

координаты векторов ē_i = (e_1i, e_2i ) – из системы однородных уравнений

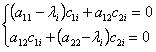, i = 1,2­ ­ ­

(9.13)

Напомним, что векторы ē₁ и ē₂ должны быть нормированными (единичной длины), поэтому, найдя произвольное решение системы (9.13) – (c_1i, c_2i ) в качестве собственного вектора следует взять:
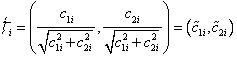, i = 1,2.
Нумерацию собственных векторов всегда можно выбрать так, чтобы поворот от ē₁ к ē₂, совершался против часовой стрелки. Тогда можно считать, что новый базис ē₁, ē₂ получается из старого 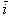, 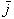поворотом на некоторый угол φ (рис. 9.1).

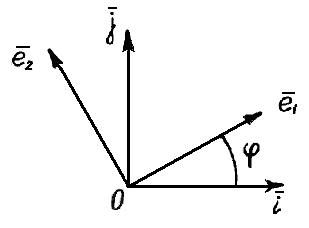
Рис.9.1. Взаимное расположение базисов 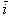, 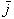и ē₁, ē₂.

Введем в рассмотрение матрицу T, столбцы которой являются координатами собственных векторов:

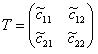
Тогда старые координаты x, y в базисе ē₁, ē₂ и новые x′, y′ в базисе ē₁, ē₂, связаны соотношениям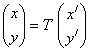и:

или ­ ­ ­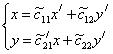

(9.14)

С помощью формул (9.14) делаем замену переменных x, y на x′, y′ в уравнении (9.9). После преобразований мы придем к уравнению вида

λ1x′ 2 + λ2 y′ 2 + 2b1 x′ + 2b2 y′ + b = 0­ ­ ­

(9.15)

Уравнение (9.15) можно исследовать способом выделения полных квадратов, а затем заменой переменных, соответствующей параллельному переносу начала координат.

Содержание типового расчета

Условие типового расчета содержит симметрическую матрицу линейного оператора A размером 3х3, а также уравнение кривой второго порядка. Необходимо:
1. Найти собственные значения и собственные векторы линейного оператора. Провести контроль расчетов, используя определение собственного значения и собственного вектора, а также проверив ортогональность полученных собственных векторов. Составить матрицу перехода к базису из найденных собственных векторов, преобразовать матрицу оператора A к новому базису.
2. Привести уравнение кривой второго порядка к каноническому виду и изобразить эту кривую на плоскости.