Классификация языков и грамматик по хомскому

Формальная грамматика – это математическая система, определяющая язык посредством порождающих правил.
Определение 1.9. Формальной грамматикой называется четверка вида:

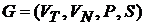, (1.1)

где VN- конечное множество нетерминальных символов грамматики (обычно прописные латинские буквы);
VT - множество терминальных символов грамматики (обычно строчные латинские буквы, цифры и т.п.),VT ÇVN =Æ;
Р - множество правил вывода грамматики, являющееся конечным подмножеством множества (VT ÈVN)+ ´(VT ÈVN)*; элемент (a, b) множества Р называется правилом вывода и записывается в виде a®b(читается: «из цепочкиa выводится цепочка b»);
S - начальный символ грамматики, S принадлежащий N.

Классификация грамматик в иерархии американского математика Хомского осуществляется по структуре правил вывода. В расширенной иерархии Хомского выделяется четыре типа грамматик.

Тип 0. Грамматика 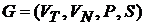называется грамматикой типа 0 (грамматикой без ограничений или грамматикой с фразовой структурой), если на ее правила вывода не наложено никаких ограничений, кроме тех, которые указаны в определении грамматики.

Тип 1.Грамматика 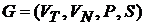называется контекстно-зависимой грамматикой (КЗ-грамматикой), если каждое правило вывода из множества Р имеет вид a®b, где aÎ (VT È VN)+, b Î (VT È VN)* и |a| £ |b|. Расширение допускает не более одного e-правила, т.е. правила вида А®e, АÎVN.
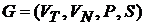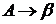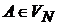Тип 2. Грамматика называется контекстно-свободной грамматикой (КС-грамматикой), если ее правила вывода имеют вид: , где и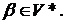
Тип 3.Грамматика 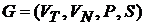называется регулярной грамматикой (Р-грамматикой), выровненной вправо, если ее правила вывода имеют вид , где .
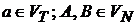Грамматика 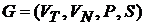называется регулярной грамматикой (Р-грамматикой), выровненной влево, если ее правила вывода имеют вид 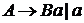, где .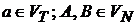

Расширение допускает единственное e-правило вида S®e, но в этом случае начальный символ грамматики S не должен встречаться в правых частях правил.

Определение 1.15. Язык L(G) называется языком типа k, если его можно описать грамматикой типа k, где k – максимально возможный номер типа грамматики.
Пример 1.7.ЯзыквидаL={0n1n | n>0} порождается КЗ-грамматикой (тип 1) G1 (пример 1.4) и КС-грамматикой (тип 2) G2= ({0, 1}, {S}, P2, S), где
множество правил вывода P2 содержит правила вида S® 0S1|01.
Так как не существует регулярной грамматики (тип 3), порождающей данный язык, то язык L является языком типа 2 или КС-языком.
Соотношение типов грамматик и языков представлено на рисунке 1.1.

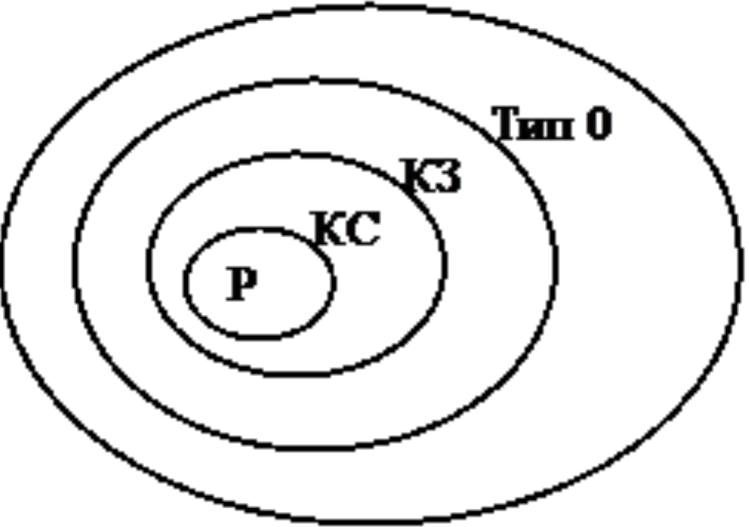
Р – регулярная грамматика;КС – контекстно-свободная грамматика;

КЗ – контекстно-зависимая грамматика;
Тип 0 – грамматика типа 0.

Рисунок 1.1 – Соотношение типов формальных языков и грамматик

Пример 1.8. Примеры различных типов формальных языков и грамматик по классификации Хомского. Терминалы будем обозначать строчными символами, нетерминалы – прописными буквами, начальный символ грамматики – S.

а) Язык типа 0 L(G)= 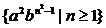определяется грамматикой с правилами вывода:

• 1) S ® aaCFD;
• 2) AD ® D;
• 3) F ® AFB | AB;
• 4) Cb ® bC;
• 5) AB ® bBA;
• 6) CB ® C;
• 7) Ab ® bA;
• 8) bCD ® e.

б) Контекстно-зависимый язык L(G)={anbncn | n³1} определяется грамматикой с правилами вывода:

• 1) S ® aSBC | aBC;
• 2) CB ® BC;
• 3) aB ® ab;
• 4) bB ® bb;
• 5) bC ® bc;
• 6) cC ® cc.

в) Контекстно-свободный язык L(G)={(aс)n(cb)n | n>0} определяется грамматикой с правилами вывода:

• 1) S ® aQb | accb;
• 2) Q ® cSc.

г) Регулярный язык L(G)={w^ | wÎ{a, b}+, где нет двух рядом стоящих а} определяется грамматикой с правилами вывода:

• 1) S ® A^ | B^;
• 2) A ® a | Ba;
• 3) B ® b | Bb | Ab.

Определение 1.16.Грамматики G1 и G2 называются эквивалентными, если они определяют один и тот же язык, т.е. .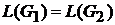
Определение 1.17.Грамматики G1 и G2 называются почти эквивалентными, если заданные ими языки различаются не более чем на пустую цепочку символов, т.е. .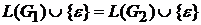
Пример 1.9.Для грамматики G1 эквивалентной будет грамматика G2 = ({0, 1}, {S}, P3, S), где P2: S® 0S1|01, т.к. L(G1)=L(G2)={0n1n | n>0} (пример 1.7).

Почти эквивалентной для грамматики G1 будет грамматика G3 = ({0, 1}, {S}, P3, S), где множество правил вывода P3 содержит правила вида S® 0S1|e, т.к. L(G3)={0n1n | n³0}.