Операции над пределами последовательностей
1. Предел суммы (разности) двух сходящихся последовательностей равен сумме (соответственно, разности) их пределов:
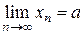 ,
, 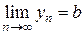

 .
.
2. Предел произведения двух сходящихся последовательностей равен произведению их пределов:
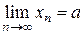 ,
, 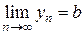

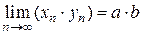 .
.
В частности:
· постоянный множитель можно выносить за знак предела:
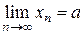 ,
, 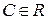

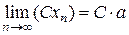 ;
;
· предел натуральной степени от сходящейся последовательности равен этой степени от ее предела:
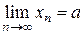

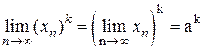 ,
, 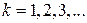
3. Предел частного двух сходящихся последовательностей равен частному их пределов:
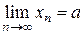 ,
, 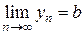
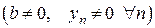

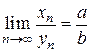 .
.
4. Предел корня к – й степени от сходящейся последовательности равен корню этой же степени от предела последовательности:
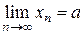 ,
, 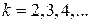

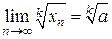 .
.
Отметим, что пределы переменных, стоящие в левых частях операций (1) – (3), могут существовать без того, чтобы существовали отдельно пределы 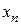 и
и 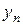 .
.
Например, если
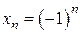 ,
, 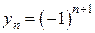 ,
,
то 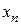 и
и 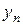 не имеют пределов, в то время как
не имеют пределов, в то время как
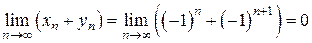 ,
,
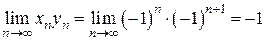 .
.
Операции над пределами во многих случаях дают возможность узнать, имеет ли числовая последовательность предел и чему он равен, если она есть результат конечного числа арифметических действий над несколькими другими последовательностями, существование и величина пределов которых известны.
Неопределенности различного вида
Пусть даны две последовательности  ,
, 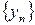 и
и 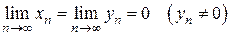 . Рассмотрим отношение этих последовательностей. О пределе этого отношения последовательностей заранее ничего определенного сказать нельзя, так как в зависимости от самих последовательностей предел их отношения может принимать различные значения. Например:
. Рассмотрим отношение этих последовательностей. О пределе этого отношения последовательностей заранее ничего определенного сказать нельзя, так как в зависимости от самих последовательностей предел их отношения может принимать различные значения. Например:
если  ,
,  , то
, то  ;
;
если 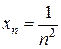 ,
, 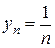 , то
, то 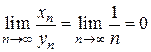 ;
;
если 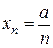 ,
, 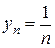 , то
, то 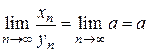 ;
;
если 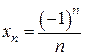 ,
, 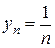 , то
, то 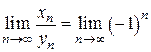 ,
,
а этот предел не существует.
Таким образом, для нахождения предела последовательности 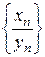 недостаточно знать, что
недостаточно знать, что 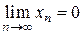 ,
, 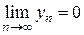 . Нужны еще дополнительные сведения о характере изменения
. Нужны еще дополнительные сведения о характере изменения  и
и 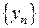 .
.
Для нахождения этого предела в каждом конкретном случае требуются специальные приемы.
Возникают неопределенности различного вида.
1.Если 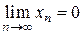 ,
, 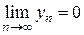 , то говорят, что выражение
, то говорят, что выражение 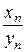 представляет собой неопределенность вида
представляет собой неопределенность вида 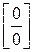 .
.
2.Если  ,
, 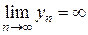 , то выражение
, то выражение 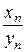 также представляет собой неопределенность и ее называют неопределенностью вида
также представляет собой неопределенность и ее называют неопределенностью вида 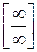 .
.
3.Если 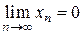 ,
, 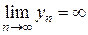 , то для выражения
, то для выражения  получаем неопределенность вида
получаем неопределенность вида 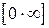 .
.
4.Если 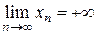 ,
, 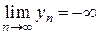 , то выражение
, то выражение 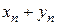 представляет собой неопределенность вида
представляет собой неопределенность вида 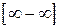 .
.
Раскрыть соответствующую неопределенность – это значит найти предел (если он существует) соответствующего выражения.
§3. Неопределенность вида 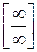
Правило.Чтобы раскрыть неопределенность вида 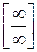 надо числитель и знаменатель почленно разделить на переменную величину в наибольшей степени.
надо числитель и знаменатель почленно разделить на переменную величину в наибольшей степени.
Пример 1.
Вычислить предел числовой последовательности
 .
.
Решение.
Дробь 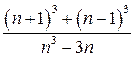 - есть отношение двух бесконечно больших величин, о котором без исследования ничего определенного сказать нельзя –неопределенность вида
- есть отношение двух бесконечно больших величин, о котором без исследования ничего определенного сказать нельзя –неопределенность вида  . Здесь также нельзя применить теорему о пределе частного, так как в условии этой теоремы предполагается, что пределы числителя и знаменателя существуют, а в нашем случае при
. Здесь также нельзя применить теорему о пределе частного, так как в условии этой теоремы предполагается, что пределы числителя и знаменателя существуют, а в нашем случае при 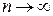
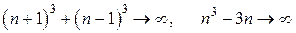 .
.
В этом случае поступают так: числитель и знаменатель дроби делят на наивысшую степень n,встречающуюся в членах дроби (в данном случае на n  ).
).
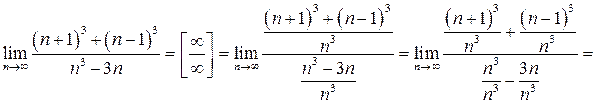

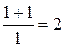 .
.
 .
.
Ответ:  .
.
Пример 2.
Вычислить предел числовой последовательности
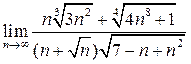 .
.
Решение.
Здесь неопределенность вида  . Разделим числитель и знаменатель дроби на наивысшую степень n, встречающуюся в дроби, т.е. на
. Разделим числитель и знаменатель дроби на наивысшую степень n, встречающуюся в дроби, т.е. на 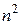 :
:
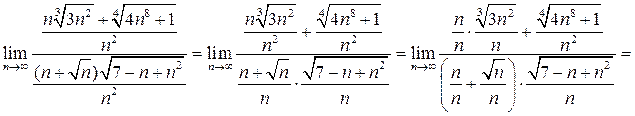
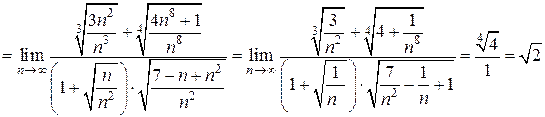 .
.
 .
.
Ответ: 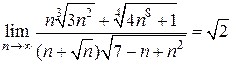 .
.
Пример 3.
Вычислить предел 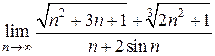 .
.
Решение.
При 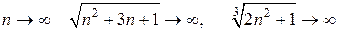 ,
,
т.е. возникает неопределенность вида 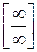 .
.
Последовательность sin n ограничена ( 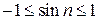 ).
).
Разделим числитель и знаменатель дроби на n
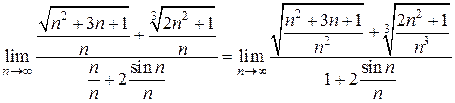 =
=
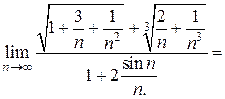
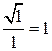 ,
,
т.к. 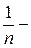 бесконечно малая последовательность при
бесконечно малая последовательность при 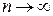 и произведение бесконечно малой последовательности на ограниченную – есть бесконечно малая последовательность, поэтому
и произведение бесконечно малой последовательности на ограниченную – есть бесконечно малая последовательность, поэтому 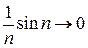 при
при 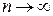 .
.
Ответ:
 .
.
§4. Неопределенность вида 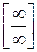 в случае арифметической, геометрической прогрессий и факториалов
в случае арифметической, геометрической прогрессий и факториалов
Правило 1.
Чтобы раскрыть неопределенность вида 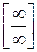 в случае арифметической прогрессии надо воспользоваться формулой суммы первых n членов арифметической прогрессии:
в случае арифметической прогрессии надо воспользоваться формулой суммы первых n членов арифметической прогрессии: 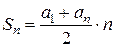 .
.
Пример 1.
Вычислить предел числовой последовательности
 .
.
Решение.
В знаменателе стоит сумма членов арифметической прогрессии. Воспользуемся формулой суммы первых n членов арифметической прогрессии.
В нашем случае 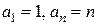 , тогда
, тогда
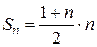 .
.
Получаем,  =
= 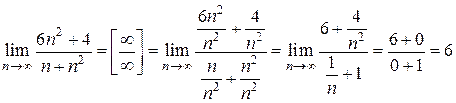 .
.
Ответ:
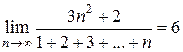 .
.
Правило 2.
Чтобы раскрыть неопределенность вида 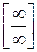 в случае геометрической прогрессии надо воспользоваться формулой суммы первых n членов геометрической прогрессии:
в случае геометрической прогрессии надо воспользоваться формулой суммы первых n членов геометрической прогрессии: 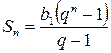 .
.
Пример 2.
Вычислить предел числовой последовательности
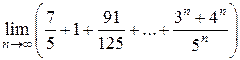 .
.
Решение.
Данная последовательность представляет собой сумму двух геометрических прогрессий:
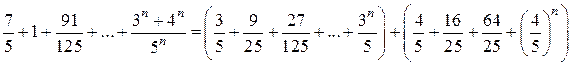 .
.
Применим формулу суммы первых n членов геометрической прогрессии. Для первой прогрессии 
для второй прогрессии 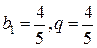 .
.
Имеем,
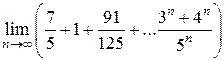 =
=
= 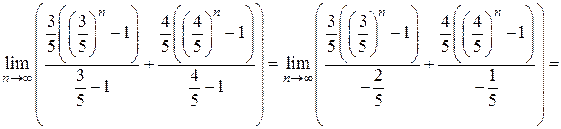

т.к. если число 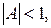
то  при
при 
Ответ:
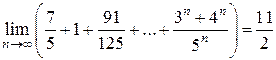 .
.
Правило 3.
Чтобы раскрыть неопределенность вида 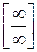 в случае факториалов надо выразить все факториалы последовательности через наименьший и сократить на него.
в случае факториалов надо выразить все факториалы последовательности через наименьший и сократить на него.
Пример 3.
Вычислить предел числовой последовательности
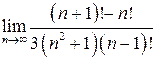 .
.
Решение.
По определению 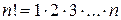 ,
,
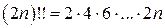 ,
,
 .
.
Поэтому, числитель и знаменатель стремятся к 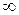 , т.е. мы имеем неопределенность вида
, т.е. мы имеем неопределенность вида 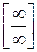 . Выберем наименьший факториал и выразим через него все остальные. В нашем примере наименьшим будет
. Выберем наименьший факториал и выразим через него все остальные. В нашем примере наименьшим будет 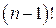 . Тогда
. Тогда 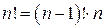 ,
,  . Имеем
. Имеем

Здесь  при
при 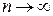 .
.
Ответ:  .
.
§5. Неопределенность вида 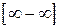
Правило.
Неопределенность вида 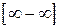 , получающаяся в результате алгебраической суммы иррациональных выражений, устраняется или приводится к типу
, получающаяся в результате алгебраической суммы иррациональных выражений, устраняется или приводится к типу 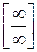 путем домножения и деления на одно и то же выражение, приводящее к формулам сокращенного умножения. В случае квадратных корней последовательность домножается на сопряженное выражение и применяется формула
путем домножения и деления на одно и то же выражение, приводящее к формулам сокращенного умножения. В случае квадратных корней последовательность домножается на сопряженное выражение и применяется формула 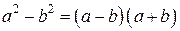 . В случае кубических корней последовательность домножается на неполный квадрат суммы или разности и применяется формула
. В случае кубических корней последовательность домножается на неполный квадрат суммы или разности и применяется формула 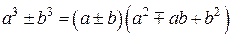 .
.
Пример 1.
Вычислить предел числовой последовательности
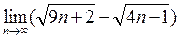 .
.
Решение.
При вычислении данного предела мы не мажем применить теорему о пределе разности двух переменных, ибо эта теорема верна только в том случае, когда обе переменные имеют предел. В нашем случае при 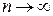
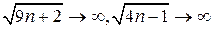 , и мы имеем дело с разностью двух положительных бесконечно больших величин. Без специального исследования этой разности ничего определенного сказать нельзя, т.е. имеем неопределенность
, и мы имеем дело с разностью двух положительных бесконечно больших величин. Без специального исследования этой разности ничего определенного сказать нельзя, т.е. имеем неопределенность 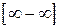 . Данная неопределенность раскрывается путем избавления от иррациональности. Вспоминая формулу
. Данная неопределенность раскрывается путем избавления от иррациональности. Вспоминая формулу 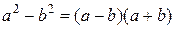 , умножим и разделим выражение
, умножим и разделим выражение 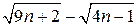 на сопряженное
на сопряженное 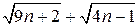 .
.

После преобразований получили дробь, у которой числитель и знаменатель бесконечно большие последовательности ( 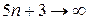 ,
, 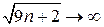 ,
, 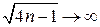 , а следовательно, и
, а следовательно, и 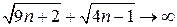 ). Возникает неопределенность
). Возникает неопределенность 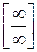 , которая раскрывается путем деления числителя и знаменателя на n в наибольшей степени, в нашем случае на n.
, которая раскрывается путем деления числителя и знаменателя на n в наибольшей степени, в нашем случае на n.
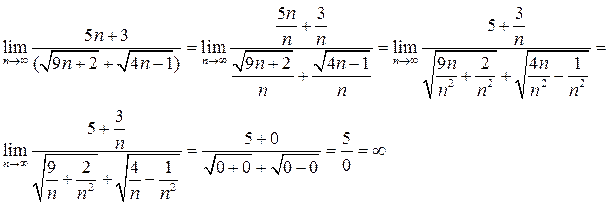
так как при 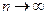 предел числителя равен 5, а знаменатель есть величина бесконечно малая, как сумма двух бесконечно малых величин. Т.е. мы имеем дело с величиной, которая обратна бесконечно малой, а такая величина есть бесконечно большая.
предел числителя равен 5, а знаменатель есть величина бесконечно малая, как сумма двух бесконечно малых величин. Т.е. мы имеем дело с величиной, которая обратна бесконечно малой, а такая величина есть бесконечно большая.
Ответ:
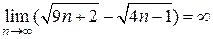 .
.
Пример 2.
Вычислить предел числовой последовательности
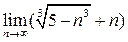 .
.
Решение.
При 
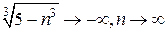 , поэтому имеем дело с неопределенностью вида
, поэтому имеем дело с неопределенностью вида 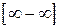 .
.
Для раскрытия неопределенности применим формулу  .
.
Положим 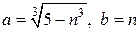 , а затем умножим и разделим на неполный квадрат разности выражения
, а затем умножим и разделим на неполный квадрат разности выражения 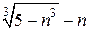 . Имеем,
. Имеем,
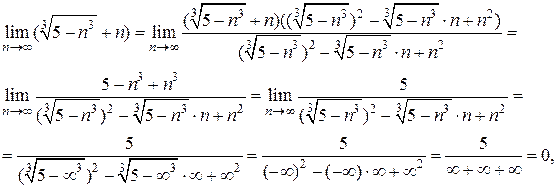
т.к. знаменатель дроби при 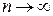 есть сумма трех положительных бесконечно больших величин, а поэтому есть величина бесконечно большая. Величина же, обратная бесконечно большой, есть величина бесконечно малая, предел которой равен нулю.
есть сумма трех положительных бесконечно больших величин, а поэтому есть величина бесконечно большая. Величина же, обратная бесконечно большой, есть величина бесконечно малая, предел которой равен нулю.
Ответ:  .
.
