Тұрақтылық аудандарын көрсету
Жоғарыда қарастырылған тұрақтылық критерияларының көмегімен параметрлері берілген автоматты реттеу жүйесі тұрақты ма жоқ па екенін анықтауға болады. Дегенмен критерийлер жүйе тұрақты болып қалуы үшін сол параметрді немесе екі параметрді бір мезгілде қандай аралықта ауыстыруға болатынын анықтап алмайды. мұны тек күшейту коэффициентіне қатысты кейбір тұрақтылық критерилердің көмегімен айтуға болады.
Тұрақтылық аудандарын көрсету мәселесімен алғашқы рет И.Л. Вышнеградский айналысты. Ол бұл мәселені үшінші реттегі дифференциялды теңдеулермен жазылған жүйелерге қатысты шешіп береді.
1947 ж. Ю.И. Неймарк сызықтандырылған жүйелердің тұрақтылық аймағын бір комплексті немесе екі нақты параметрлер бойынша кез – келген ретті дифференциялдық теңдеулермен берілген жүйелер үшін көрсету әдісін ойлап тапты. Бұл әдіс Д – бөлшектеудің мәні төмендегідей. Екі коэффициенттен бөлек (мысалы, 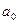 және
және  ) барлық коэффициенттері белгілі және өзгермейді.
) барлық коэффициенттері белгілі және өзгермейді.
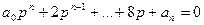 (5.21)
(5.21)
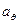 мен
мен 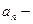 ң кейбір мәндері түбірдің бір бөлігі
ң кейбір мәндері түбірдің бір бөлігі 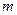 санымен оң жақ компелекстік жазықтықта, ал екінші бөлігі
санымен оң жақ компелекстік жазықтықта, ал екінші бөлігі 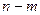 санымен сол жақ комплекстік жазықтықта жатыр дейік. 5.12. суретте түбірлердің жалпы саны
санымен сол жақ комплекстік жазықтықта жатыр дейік. 5.12. суретте түбірлердің жалпы саны 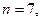
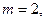
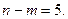
Алгебралық теңдеу коэффициенттері мен олардың түбірлерінің комплекстік жазықтықта тармақталуының арасында үздіксіз тәуелділік бар екені белгілі. Теңдеу коэффициенттерінің мәнін өзгерткен кезде түбірлердің жазықтықтағы күйі өзгереді. Коэффициенттердің тізбектеп өзгерткеннен нақты түбірлердің біреуі немесе екі тұтасқан комплекстік түбірлержорамал өсьне түседі, ал содан кейін басқа жартылай жазықтыққа өтеді, және осылай, түбірлердің жарты жазықтықтар арасында тармақталуы өзгереді. 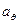 және
және  коэффициент мәндерін өзгерте отырып, барлық түбірлердің сол жақ комплекстік жартылай жазықтыққа орналасып, жүйе тұрақты болуына қол жеткізуге болады.
коэффициент мәндерін өзгерте отырып, барлық түбірлердің сол жақ комплекстік жартылай жазықтыққа орналасып, жүйе тұрақты болуына қол жеткізуге болады.
Дегенмен коэффициенттерді түбірлер орын ауыстыра отырып, сол жазықтықта қалатын шектерде әрқашан өзгертуге болады, және сонда, түбірлердің тармақталуы бұрынғыдай болып қалады. 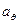 және
және  коэффициентерінің жазықтығында осы коэффициентердің мәндерінің аймағын көрсетуге болады, ол кезде барлық түбірлер сол жақ комплекстік жазықтықта орналасып, жүйе тұрақты күйінде қалады. осы тұрақтылық аймағы. Осы аймақтан тыс шығып кеткен коэффициентердің мәндерінде жүйе тұрақтылығын жоғалтады. Тұрақтылық аймағының шекарасы болып ең болмағанда бір түбірі жорамал өсьте орналасатын коэффициенттер мәндері болып табылады.
коэффициентерінің жазықтығында осы коэффициентердің мәндерінің аймағын көрсетуге болады, ол кезде барлық түбірлер сол жақ комплекстік жазықтықта орналасып, жүйе тұрақты күйінде қалады. осы тұрақтылық аймағы. Осы аймақтан тыс шығып кеткен коэффициентердің мәндерінде жүйе тұрақтылығын жоғалтады. Тұрақтылық аймағының шекарасы болып ең болмағанда бір түбірі жорамал өсьте орналасатын коэффициенттер мәндері болып табылады.
Осыдан, тұрақтылық шекарасы комплекстік жазықтықтың жорамал өсінің коэффициенттері өсінде бейнеленуі болып табылады. 5.13. суретте коэффициенттер жазықтығындағы 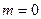 (яғни оң жақ жартылай жазықтықта түбірлер жоқ) тұрақтылық аймағы болып табылатын аймақ көрсетілген.
(яғни оң жақ жартылай жазықтықта түбірлер жоқ) тұрақтылық аймағы болып табылатын аймақ көрсетілген.
Д– бөлшектеу ұғымын түсіне отырып, тұрақтылық аймағын бір параметр бойынша (комплекстіктің жеке жағдай болып, табылатын комплекстіге немесе нақтыға) және екі нақты параметр бойынша көрсетудің ережелерін қарастыруға өтеміз.
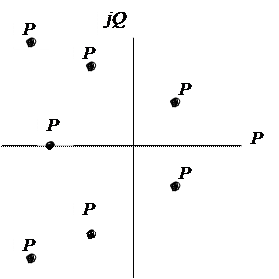
5.12. Сурет. Түбірлердің комплекстік жазықтықта тармақталуы
Бір парамтер жазықтықты Д – бөліктеу.Кез – келген Б параметрі (мысалы, уақыт тұрақтысы) сипаттамалы теңдеудің бірнеше коэффициенттеріне сызықты түрде (бір дәрежеде) кіреді, бұл жағдайда оны мына түрде жазуға болады. 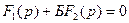 (5.22)
(5.22)
|
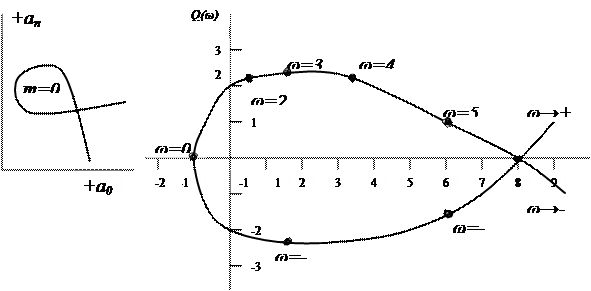
5.13. Сурет. Параметрлер 5.14. Сурет. Бір параметрді Д – бөлшектеу
жазықтығын Д– бөлшектеу мысалы
Б параметрін айнымалы деп есептейік. Әдетте ол нақты сандардың жанында беріледі. Бұл сандарды өзінің жазықтығы бар комплексті деп санауға болады, ол жазықтықта түбірлер жазықтығының жорамал өсі беріледі. (5.22) өрнегіненаламыз 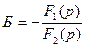 (5.23)
(5.23)
Ең болмағанда бір түбірі жорамал жазықтықта орналасатын Б параметрінің мәнін алу
үшін (5.23) өрнектегі p операторын jw жорамал сонмен алмастырып, алынған комплекстік
санда нақты және жорамал бөлігін ажыратамыз. 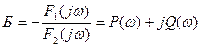 (5.24)
(5.24)
Барлық мүмкін жорамал түбірлерге сәйкес келетін Б параметрлерінің барлық мүмкін мәндерін алу үшін (5.24) өрнекке 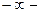 тен +
тен +  ке дейінгі аралықтағы W мәндерін беріп, P(W) мен Q(w) – ң сәйкес мәндерін есептеп шығарамыз, және осы координаттарда түбірлер жазықтығының жорамал өсінің Б параметрінің комплекстік жазықтықтағы бейнесі, немесе Б параметрі бойынша Д – бөлшектеудің шекарасы болып табылатын сызықтық құрамыз (5.14. сурет).
ке дейінгі аралықтағы W мәндерін беріп, P(W) мен Q(w) – ң сәйкес мәндерін есептеп шығарамыз, және осы координаттарда түбірлер жазықтығының жорамал өсінің Б параметрінің комплекстік жазықтықтағы бейнесі, немесе Б параметрі бойынша Д – бөлшектеудің шекарасы болып табылатын сызықтық құрамыз (5.14. сурет).
Тұрақты жүйеде барлық түбірлер, егер - 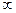 – тен +
– тен +  ке дейінгі бағытта қозғалысқа жорамал өсьтің сол жағында орналасады. Д – бөлшектеу сызығы жорамал өсьтің бейнесі болғандықтан, тұрақтылық аймағы да, егерсол арқылы w =
ке дейінгі бағытта қозғалысқа жорамал өсьтің сол жағында орналасады. Д – бөлшектеу сызығы жорамал өсьтің бейнесі болғандықтан, тұрақтылық аймағы да, егерсол арқылы w =  мәнінен w =
мәнінен w =  мәнгедейінгі бағытта қозғалса, осы сызықтың сол жағында орналасады. Тұрақтылық аймаған беру үшін Д – бөлшектеу сызығына -
мәнгедейінгі бағытта қозғалса, осы сызықтың сол жағында орналасады. Тұрақтылық аймаған беру үшін Д – бөлшектеу сызығына - 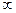 – тен +
– тен +  ке көрсетілген орын ауыстыру кезінде сол жақтан штриховка жүргізіледі.
ке көрсетілген орын ауыстыру кезінде сол жақтан штриховка жүргізіледі.
Ішінде ең көп штриховка жүргізілген аймақ тұрақтылық өсі болуы мүмкін. 5.14. сурет. бұл аймақ I. Кез – келген тұрақтылық критериясының көмегімен бізді қызықтырушы аймақта жатқан нақты өсьтің кез – келген нүктесі үшін жүйе тұрақтылығы тексеріледі.
Егер жүйе осы нүкте үшін тұрақты болса, онда бұл аймақ тұрақтылық аймағы болып табылады. Тұрақтылық аймағы болуы да мүмкін. Сәйкесінше, қарастырылып жатқан параметрдің кез – келген мәнінде жүйе тұрақсыз.
Екі нақты параметрлер жазықтығын Д – бөлшектеу. Екі жағдай болуы мүмкін: 1) параметрлер текдеуге сызықты түрде кіреді; 2) параметрлер теңдеуге бейсызықты түрде кіреді.
Сипаттамалық теңдеуге бейсызықты түрде кіретін параметрлер бір – біріне көбейтіле алмайды және дәрежелері бірден жоғары емес әдетте мұндай параметрлер болып күшейту коэффициенті мен уақыт тұрақтысының біреу болып табылады.
Сипаттамалық теңдеуге бейсызықты түрде кіретін параметрлер бір – бірімен көбейтіле алады. Әдетте мұндай параметрлер уақыт тұрақтылары болып табылады.
Б мен В парамтерлер сызықты түрде кірген жағдайда, бұл параметрлерді сипаттмалы теңдеулер жүйесінде көрсете отырып мына түрде көрсетуге болады.
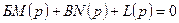 (5.25)
(5.25)
p–ны 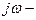 ге алмастырып және жорамал бөліктен бөліп, аламыз
ге алмастырып және жорамал бөліктен бөліп, аламыз
БМ( j  ) + BN ( j
) + BN ( j  ) +L( j
) +L( j  ) = Б
) = Б 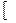 М1(
М1(  )+ jМ2 (
)+ jМ2 (  )
) 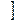 +
+
+B 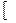 N1(
N1(  )+ jN2(
)+ jN2(  )
) 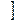 +
+ 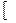 L1(
L1(  )+ jL2(
)+ jL2(  )
) 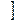 =0, (5-26)
=0, (5-26)
осыдан
P(  )=БМ1(
)=БМ1(  )+BN1(
)+BN1(  )+L1(
)+L1(  ) = 0 ;
) = 0 ;
Q(  ) = БМ2(
) = БМ2(  )+BN2(
)+BN2(  )+L2(
)+L2(  )=0. (5-27)
)=0. (5-27)
Д – бөлшектеу шекарасының нүктесін табу үшін, (5.27) теңдеуін Б мен В – ға қатысты шешеміз.
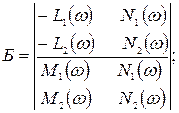
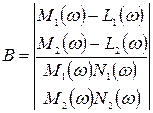 (5.28)
(5.28)
Егер мына анықтауыш
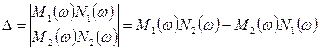 (5.29)
(5.29)
ол нөльге тең болмаса, онда  ң әрбір мәніне Б мен В – ң нақты мәндері сәйкес келеді, олар
ң әрбір мәніне Б мен В – ң нақты мәндері сәйкес келеді, олар  -
- 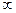 – тен +
– тен +  ке дейін үздіксіз өзгерткен кезде Б мен В параметрлер жазықтығындағы Д – бөлшектеу сызығының нүктелер координатасы болып табылады.
ке дейін үздіксіз өзгерткен кезде Б мен В параметрлер жазықтығындағы Д – бөлшектеу сызығының нүктелер координатасы болып табылады.
(5.28) өрнегі (5.27) теңдеуінде сызықты түрда тәуелсіз болып қалатын ғана  ң мәндері үшін әділетті. Соңғылары
ң мәндері үшін әділетті. Соңғылары  мен
мен 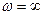 үшін сызықты тәуелсіз болып қалмайды. Сондықтан (5.28) өрнегімен ерекше сызықтармен толықтырылатын Д – бөлшектеудің теңдеулері
үшін сызықты тәуелсіз болып қалмайды. Сондықтан (5.28) өрнегімен ерекше сызықтармен толықтырылатын Д – бөлшектеудің теңдеулері  мен
мен 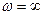 мәндерін (5.26) теңдеуге қою арқылы алынады.
мәндерін (5.26) теңдеуге қою арқылы алынады.
Мысалы. 4.1. суретте жүйені күшейту коэффициенті бойынша Д– бөлшектеуді жүргізейік, ол үшін (5.5) сипаттамалық теңдеуін пайдаланып, ондағы K күшейту коэффициентін айнымалы деп аламыз.
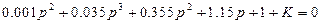 (5.37)
(5.37)
Бұл өрнектегі  ны jw-ға алмастырамыз
ны jw-ға алмастырамыз
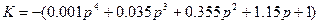
және нақты және жорамал бөліктерін бөліп аламыз
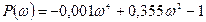 ;
;
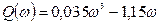 . (5-39)
. (5-39)
(5.39) өрнекке w-ң - 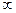 – тен +
– тен +  ке дейінгі аралықтағы әртүрлі мәндерін қойып шығып, P(w) мен Q(w) –ң сәйкес мәндерін есептеп аламыз. Есептің нәтижелері 5.3. кестеде енгізілген. 5.14. кестеде берілген берілгенднр бойынша 5.14. суретте Д- бөлшектеу сызығы салынған және егре w-ң -
ке дейінгі аралықтағы әртүрлі мәндерін қойып шығып, P(w) мен Q(w) –ң сәйкес мәндерін есептеп аламыз. Есептің нәтижелері 5.3. кестеде енгізілген. 5.14. кестеде берілген берілгенднр бойынша 5.14. суретте Д- бөлшектеу сызығы салынған және егре w-ң - 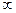 – тен +
– тен +  ке дейін өзгерген кезде оның бойымен орын ауыстырса, сол жақтан штрихтелген
ке дейін өзгерген кезде оның бойымен орын ауыстырса, сол жақтан штрихтелген
5.3 – кесте
| ω | P(ω) | Q(ω) | ω | P(ω) | Q(ω) |
| -6 | 9.044 | -0.650 | -1.000 | 0.000 | |
| -5.73 | 8.100 | 0.000 | -0.686 | -1.115 | |
| -5 | 6.335 | 1.375 | +0.244 | -2.040 | |
| -4 | 3.784 | 2.360 | 1.759 | -2.506 | |
| -3 | 1.759 | 2.506 | 3.784 | -2.360 | |
| -2 | +0.244 | 2.040 | 6.335 | -1.375 | |
| -1 | -0.686 | 1.005 | 5.73 | 8.100 | 0.000 |
| -1.000 | 0.000 | 9.044 | +0.650 |
Тұрақтылықтың ықтимал аймағы / аймағы болуы мүмкін, өйткені ол толығымен штрихтелген. Бұл шындыққа үйлеседі, өйткені басқа критериялардың көмегімен бұрын K = 4 мәнінде жүйе тұрақты екенін анықтайды.
Д – бөлшектеу қисығын қарастырғанымыздан жүйе 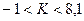 кезінде тұрақты болып қалатыны көрініп тұр.
кезінде тұрақты болып қалатыны көрініп тұр.
Негізгі әдебиет: 1 [179-195]; 2 [147-165].
Қосымша әдебиет: 1 [178-194].
Бақылау сұрақтар:
- Критикалық күшейту коэффициенті дегеніміз не.
- Найквистің амплитуда – фазалыық тұрақтылық критериясын құрып беріңіз.
- Тұрақтылықты логарифмді жиілікті сипаттамалар бойынша талдау қалай жүргізіледі.
- Қандай жағдайларда қай тұрақтылық критериясын пайдаланған қолайырақ.
№ 7 Дәрістің конспектісі
Дәрістің тақырыбы: Сызықты жүйелерді реттеу процесінің сапасын зерттеу.(Сапаның тура көрсеткіштері. Жүйенің жүйенің өтпелі процесін құру әдістері ( операторлық трапеция әдісі, модельдеу әдісі). Түбірлерді үйлестіру әдісімен сапаны зерттеу. Сапаны интегралды түрде бағалау әдісі. Сапаны жиіліктік әдіспен зерттеу).
Сапа көрсеткіштері
Реттеу процесінің сапасы деп реттеу жүйесінің параметрлері мен басқарушы және қоздырушы әсердің сапасына тәуелді тұрақты жүйенің өтпелі процесінің сипатын айтамыз.
Сапа көрсеткіштері деп жүйенің қандай – да бір типтік сыртқы әсерден (көбінесе бірлік сатылы әсер) пайда болған өтпелі процестегі әрекетін сипаттаушы шамаларды айтамыз.
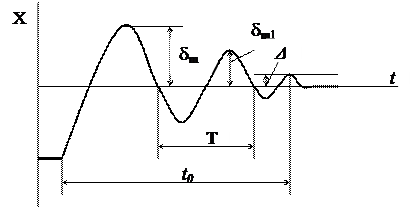
6.1. Сурет. Өтпелі процесс сапасының көрсеткіштері
Негізгі сапа көрсеткіштерін қарастырайық.
1. Реттеу уақытты t0 – реттелетін шаманың берілген мәннен ауытқуы алдында берілген 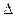 шамадан кіші болып қалады (6.1 сурет).
шамадан кіші болып қалады (6.1 сурет).
2. Қайта реттеушамалары – реттелетін шаманың жаңа берілген мәннен бастапқы мәннен бастапқы мәннен қарама – қарсы жаққа 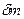 максималды ауытқуы. Реттелетін шама жаңа берілген мәнге тек бір жақтан ғана, бастапқы және жаңа берілген мәндермен шектелген аралықтан шықпай жақындаған жағдайларда қайта реттелу болмайды.
максималды ауытқуы. Реттелетін шама жаңа берілген мәнге тек бір жақтан ғана, бастапқы және жаңа берілген мәндермен шектелген аралықтан шықпай жақындаған жағдайларда қайта реттелу болмайды.
3. Орнатылған ауытқу – реттелетін шаманың орнықты процесте берілген мәннен ауытқу шамасы.
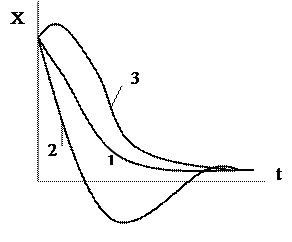
6.2. Сурет. Өтпелі процестің алуан түрлері
мұндағы А – бастапқы тербеліс амплитудысы;
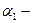 комплекстік түбірдің нақты бөлігінің мәні, 1/ сек;
комплекстік түбірдің нақты бөлігінің мәні, 1/ сек;
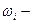 комплекстік түбірдің жорамал мәні – бұрыштық тербеліс жиілігі, 1/ сек;
комплекстік түбірдің жорамал мәні – бұрыштық тербеліс жиілігі, 1/ сек;
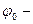 бастапқы фазаның жылжымасы; рад
бастапқы фазаның жылжымасы; рад
4. Өтпелі процестің өшіп қалу сипаты монотонды, апериодты немесе тербелісті болуы мүмкін.
Монотонды деп реттелетін шама орнықтылығын мәнге тербелу периоды әртүрлі бір екі немесе бірінеше тербелістен кейін және қайта реттеу арқылы келетін процесті айтамыз. (6.2. сурет. 2 мен 3 қисықтары).
Тербелістік процесс деп реттелетін шама орнатылған мәнге гармоникалық тербеліспен келетін процесті айтамыз (6.1. сурет).
Жоғары ретті жүйенің тербелістік процесін өшіп қалуы төмендегі заңдылықпен жүретін жеке құраушыларға бөлуге болады: 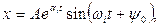 (6.1)
(6.1)
Тербеліс периодының шамасы
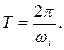
Екі көршілес максималды ауытқулар арасындағы қатынас
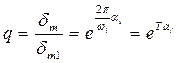 (6.2)
(6.2)
Осы қатынастың натуралды логарифмі
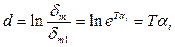 (6.3)
(6.3)
бұл логарифмді өшіпқалу декременті деп аталады.
(6.3) өрнегінен өтпелі процестің құраушыларының тербелістерінің өшіп қалу жылдамдығы сәйкес екі біріккен комплекстік түбірдің нақты бөлігінің 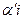 мәніне тікелей пропорционал логарифмді өшіп қалу декремента шамасынан тура тәуелділікте орналасқаны көрініп тұр.
мәніне тікелей пропорционал логарифмді өшіп қалу декремента шамасынан тура тәуелділікте орналасқаны көрініп тұр.
5. Өтпелі процестің тербелістігі – реттелетін шаманың оның жаңа орнықты шамасының жанынан тербелу саны.
Ол әдетте берілген саннан аспау керек.
Мысал. 4.1. суретте. бейнеленген автоматты реттеу жүйесінің (5.5) сипаттамалық теңдеуінің түбірлерін табамыз. 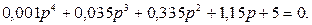
Теңдеуді жоғары дәрежедегі коэффициентке бөлеміз
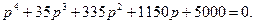 (6.6)
(6.6)
Осы теңдеудің соңғы 3 мүшелерінен квадраттық теңдеу құрамыз
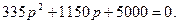
Бұл теңдеуді жоғары дәрежедегі коэффициентке бөліп, мынаны аламыз
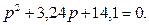 (6.7)
(6.7)
Бұл квадраттық теңдеудің түбірлері комплексті. Бұл теңдеуді бірінші жорамал деп есептеп, оған (6.6) теңдеуді бөлеміз
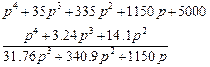
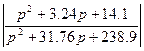
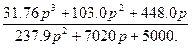
Разделив трехчлен, полученный в остатке, на коэффициент при р, получим второе приближение
p 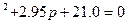
и делим на него уравнение (6-6)
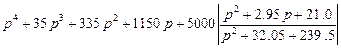

--
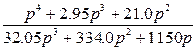
--
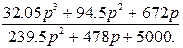
239,5 –ке бөліп, үшінші жақындықты аламыз 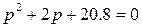
Оған, (6.6) –ны бөлеміз. Есепті осыған ұқсас жүргізе отырып, төртінші, содан кейін бесінші жақындықты да аламыз.
және 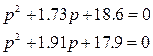 (6.8)
(6.8)
Алтыншы жақындық
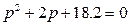 (6.9)
(6.9)
ол бесіншіден аз ғана ерекшеленеді және сондықтан осыдан тоқтаймыз.
Бұл теңдеудің түбірлері 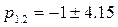 j.
j.
(6.6) басқарудың келесі түбірлері соңғы бөлу кездегі жеке түрде алынған 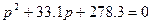 басқару түбірлерін береді.
басқару түбірлерін береді.
Бұл түбірлерді анықтаймыз 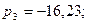
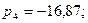
Қарастырылған жүйе үшін тұрақтылық дәрежесі, яғни жорамалдан жақын түбірге дейінгі ара – қашықтығы α =-11/сек. Тұрақтылық дәрежесінің 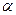 шамасы бойынша реттеу уақытын анықтауға болады, егер жүйенің өшіп қалу уақытын жорамал өське жақын түбірмен анықталатын құраушылардың өшіп қалу уақытына шамамен тең деп алсақ. Мұны (6.3) өрнегінің көмегімен, оған көршілес амплитудалар
шамасы бойынша реттеу уақытын анықтауға болады, егер жүйенің өшіп қалу уақытын жорамал өське жақын түбірмен анықталатын құраушылардың өшіп қалу уақытына шамамен тең деп алсақ. Мұны (6.3) өрнегінің көмегімен, оған көршілес амплитудалар 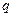 қатынасының орнына бастапқы мен соңғы ауытқулар қатынасын
қатынасының орнына бастапқы мен соңғы ауытқулар қатынасын 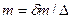 , қоя отырып (6.1. сурет), ал ондағы Т тербеліс перидының орнына t0, реттеу уақытын,
, қоя отырып (6.1. сурет), ал ондағы Т тербеліс перидының орнына t0, реттеу уақытын, 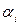 тұрақтылық дәрежесінің орнына
тұрақтылық дәрежесінің орнына 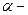 ны қоя отырып жасауға болады. Түрлендіру нәтижесінде аламыз.
ны қоя отырып жасауға болады. Түрлендіру нәтижесінде аламыз.
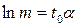 , (6.10)
, (6.10)
осыдан реттеу уақыты
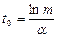 (6.11)
(6.11)
Қарастырылған мысал үшін қайта реттеуді азайтудың берілген қысқалығы 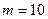 болған кездегі реттеу табамыз.
болған кездегі реттеу табамыз.
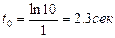 (6.12)
(6.12)
Реттелу уақытын шамамен анықтау қаншалықты ықтималды болып табылатынын тексерейік. Ол үшін (6.9) сипаттмалық теңдеу сәйкес келетін екінші ретті дифференциалдық теңдеуді шешеміз. Бұл теңдеуді (4.28) теңдеуінің көмегімен алуға болады, егер сол жақтағы жақша ішіне (6.9) сипаттмалық теңдеуді, ал оң жағын өзгеріссіз қалдырсақ. Оң жақтағы минусты жібереміз. Лаплас түрлендіру кезінде 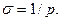
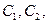 және
және 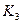 мәндерін §5.2 мысалының берілгендері бойынша есептеп аламыз. (4.28) теңдеуінің оң жақ бөлігін сол жақ бөлігі бөлінген p кездегі коэффициентке бөлеміз. Барлық табылған мәндердің қойылымынан кейін, аламыз.
мәндерін §5.2 мысалының берілгендері бойынша есептеп аламыз. (4.28) теңдеуінің оң жақ бөлігін сол жақ бөлігі бөлінген p кездегі коэффициентке бөлеміз. Барлық табылған мәндердің қойылымынан кейін, аламыз.
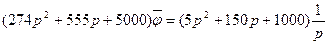
осыдан 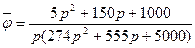 (6.13)
(6.13)
Бейнеден оригиналға өте отырып, аламыз
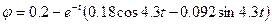 (6.14)
(6.14)

6.3. Сурет. Жеңілдетілген дифференциялды теңдеу шешімі бойынша тұрғызылған өтпелі процестің қисығы
(6.14) өрнегі қарастырғаннан, жаңа орнатылған мәннен максималды ауытқуы 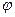 0,12- ге тең екені көрініп тұр. 2,6 сек-тан кейін жаңа орнатылған мәннен
0,12- ге тең екені көрініп тұр. 2,6 сек-тан кейін жаңа орнатылған мәннен 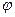 ауытқудың амплитудалық мәні
ауытқудың амплитудалық мәні 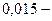 ті құрайды, осыдан
ті құрайды, осыдан 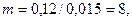 ал 2,3 сек-тан кейінгі ауытқу 0б01- болады. Бұл берілгендер (6.12) өрнегі бойынша алынған нәтижелермен жеткілікті түде келіседі. Тұрақтылық дәрежесін
ал 2,3 сек-тан кейінгі ауытқу 0б01- болады. Бұл берілгендер (6.12) өрнегі бойынша алынған нәтижелермен жеткілікті түде келіседі. Тұрақтылық дәрежесін 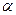 сонымен қатар сипаттамалық теңдеудің түбірін таппай – ақ анықтауға болады, дегенмен осы кездегі есептеулер сонша күрделі болып келеді, сондақтан бұл тәсілді пайдалану ұсынылмайды.
сонымен қатар сипаттамалық теңдеудің түбірін таппай – ақ анықтауға болады, дегенмен осы кездегі есептеулер сонша күрделі болып келеді, сондақтан бұл тәсілді пайдалану ұсынылмайды.
Тербелістік анықтау тәсілін қарастырайық. Жүйедегі тербелістер сипаттамалық теңдеулер түбірінің арасында мына түрдегі 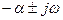
біріккен комплекстік түбірлері бар болған жағдайда қадағаланады.
Тербелістік комплекстік түбірдің жорамал бөлігінің нақты бөлігіне қатынасымен анықталады.
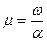
Егер сипаттамалық теңдеуде бірнеше біріккен түбірлер бар болса, онда тербелістік аса баяу берілетін ең кіші нақты бөлікті түбірлер бойынша анықталады.
Жоғарыда қарастырылған мысал үшін тербелістікті анықтаймыз. (6.5) сипаттамалық теңдеудің қосылған комплекстік түбірлері бар 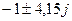
Өтпелі процестің құраушыларының тербелістігі мына түбірлерге сәйкес келеді 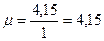
Ол өтпелі процестегі реттелетін шама орнықты мәнге келуден алдын одан төрт рет өтеді (6.3. сурет).
Негізгі әдебиет:
Қосымша әдебиет:
Бақылау сұрақтар:
1. Автоматты реттеу жүйесінің негізгі сапа көрсеткіштері.
2. Автоматты реттеу жүйе сапасын зерттеудің қандай әдістері бар.
3. Сипаттамалқы теңдеу түбірлерінің клмплекстік жазықтықта тармақталуы мен жүйе сапасы арасында қандай байланыс бар.
4. Өтпелі процестің сапасына жүйенің беріліс функция нөльдері мен полюстерінің тармақталуы қалай әсер етеді.
5. Сапаны интегралды бағалаудың мәні және қандай жағдайларда қолданылады.
№8 Дәрістің конспектісі
Дәрңс тақырыбы. Сызықты жүйені реттеу процесініңсапасын зерттеу. (Тура сапа көрсеткіштері. Жүйенің өтпелі процесін құру әдістері (операторлық, трапеция әдісі, модельдеу әдісі. Түбірлерін үйлестіру әдісімен сапаны зерттеу. Сапаны интегралды бағалау әдісі. Сапаны жиіліктік әдіспен зерттеу).
Өтпелі процесті анықтаудың негізгі тәсілдері
Автоматты басқару жүйесін есептеуді аяқталған кезде, тұрақтылығы мен берілген қиғаш (жанама) сапа көрсеткіштері,н қамтамасыз ету шартында құрылымы мен жүйе параметрлерінің мәндері таңдап алынған процесінде (өтпелі процесс уақыты, қайиа реттеу шамасы және т.б.). Әдетте кез – келген типтік әсерден жүйелегі өтпелі процестің қисығы болжаммен тұрғызылады.
Жүйенің аса сипатты жұмыс істеу режимінің өтпелі процестерін әртүрлі анықтау әдістерін (шығыс шама мен қателіктің уақыт бойынша өзгеру графигінің түрінде) екі негізгі топқа бөлуге болады.
Бірінші топқа басқару жүйесінің дифференциялды теңдеуін шамамен шешудің әртүрлі (аналитикалық, графикалық, графоаналитикалық) тәсілдері кіреді, олардың ең көп тарағаны Лаплас түрлендіруін пайдалануға негізделген операторлық әдісі болып табылады.
Екінші топты автоматты басқару жүйесінің жиіліктік сипаттмасын пайдалануға негізделген әдістер құрайды. Мұнда ең танымалы трапеция тәріздеснақты жиіліктік сипаттма көмегімен өтпелі процестің қисығын құру әдісі болып табылады.
Операторлық әдісті пайдалану негізде дифференциялды теңдеулерді (шаманың операторлық бейнесіне өту кезінде) алгебраландыру арқасында автоматты басқару жүйе теңдеуін құру процесі едәуір жеңілденеді, ол жеке үзбелердің беріліс функциясын анықтау мен басқару жүйенсінің құрылымдық схемасын түрлендіруге алып келеді.
Ф(p) тұрақталған жүйенің беріліс функциясын анықтағаннан кейін шығыс шаманың операторлық бейнесі формула негізінде мына түрде алынуы мүмкін
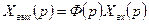
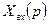 бейнесіне қатысты оригинал болып табылатын
бейнесіне қатысты оригинал болып табылатын 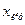 типтік кіріс әсері ретінде көбінесе бірлік (секіріс түрдегі) уақыт функциясы түрдегі әсер қолданылады.
типтік кіріс әсері ретінде көбінесе бірлік (секіріс түрдегі) уақыт функциясы түрдегі әсер қолданылады.
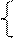 1 при t ≥ 0.
1 при t ≥ 0.
Хвх(t)=1(t) = 0 при t < 0,
оның Лаплас бойынша операторлық бейнесі 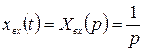
бірлік функциядан бөлек автоматты басқару жүйесін зерттеу кезіндегі типтік әсер ретінде (негізінде, қадағалау жүйенлер), сонымен қатар келесі кіріс әсерлері де қолданылады:
сызықты уақыт функциясы түрінде
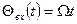 при
при 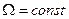 , болғанда
, болғанда
оның операторлық бейнесі 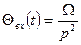
квадраттық уақыт функциясы түрінде 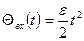
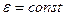 , болғанда;
, болғанда;
оның оператолық бейнесі 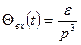
синустық уақыт функция түрінде
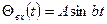 болғанда
болғанда 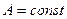 ,
, 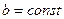 , болғанда,
, болғанда,
оның 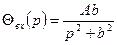
Операторлық есептеулер бойынша бірқатар басқармалардафукцияның операторлық функциясы Лаплас түрлендіруі бойынша емес, ал Карсон – Хевисойд деп аталатын түрлендіруімен анықталады, ол Лаплас интегралының алдында p көбейткішінің бар болуымен ерекшеленеді. сондақтан осы басқарушы кестелерін пайдалана отырып, барлық операторлық бейнелерді p – ға бөлу қажет.
Егер Ф (p) жүйесінің беріліс функциясы белгілі және кіріс әсері берілген болса, онда өтпелі процесті анықтау 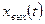 оригиналын оның
оригиналын оның 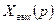 операторлық бейнесі бойынша табуға алып келеді. Осы кезде көп бөлігінде нөльдермен қабылданатын бастапқы шарттар берілуі қажет.
операторлық бейнесі бойынша табуға алып келеді. Осы кезде көп бөлігінде нөльдермен қабылданатын бастапқы шарттар берілуі қажет.
Онша жоғары емес ретті жүйелердегі оригиналдарды табу үшін операторлық бейне кестелері қолданылуы мүмкін.
Үштен жоғары ретті жүйелерде әдетте мағынасы келесі түрде қорытылатын Хейвисойдтың бөлшектеуінің екінші теоремасын қолданады. Кез – келген 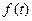 функцияның
функцияның 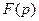 операторлық бейнесі бөлшек түрінде берілсін
операторлық бейнесі бөлшек түрінде берілсін
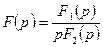
мұндағы 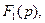
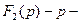 дан полиномдар.
дан полиномдар.
Сонда оригинал мына сияқты анықталуы мүмкін
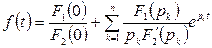
мұндағы
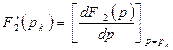
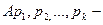 арасында қысқа және нөльдік түбірлер жоқ алгебралық теңдеулердің түбірлерінің мәні.
арасында қысқа және нөльдік түбірлер жоқ алгебралық теңдеулердің түбірлерінің мәні.
Бөлшектеу теоремасын пайдалану дифференциялды теңдеуді шешудің классикалық әдістерін қолданғанкезде қажетті тұрақты интегралдауды анықтау процедурасының күрделілігін болдырмауға мүмкіндік береді, бірақ зерттеліп жатқан басқару жүйесінің сипаттмалық теңдеуі болып табылатын 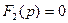 теңдеу түбірін табудан арылттырмайды.
теңдеу түбірін табудан арылттырмайды.
Сипаттмалық теңдеу түбірлерінің жорамал мәнін анықтаудың аса тиімдісі көпмүшелерді бөлу әдісі мен инерциялы әдісі болып табылады, олар мысалдарда қолданылған.
Өтпелі процесті трапециялы нақты жиіліктік сипатта көмегімен қисығын құру басқару жүйесіндегі өтпелі процесті анықтайтын 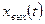 функциясы мен
функциясы мен 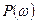 тұйықталған басқару жүйесінің беріліс функциясына
тұйықталған басқару жүйесінің беріліс функциясына  қойып алынған.
қойып алынған. 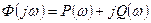
комплекстік өрнегінің нақты бөлігін беретін 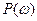 жиіліктік функция арасында бірмәнді байланыстың бар болуына негізделген.
жиіліктік функция арасында бірмәнді байланыстың бар болуына негізделген.
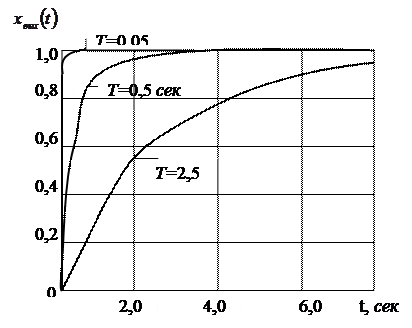
6.5 сурет. Бірлік кіріс функциясы кезіндегі инерциялы үзбенің 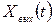 қисықтары.
қисықтары.
Қадағалау жүйелерінде өтпелі процесс көбінесе 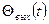 жүйенің шығыс шамасы емес,
жүйенің шығыс шамасы емес, 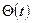 қатесінің өзгеру графигінің түрінде анықталады. Бұл жағдайда тұйықталған жүйенің беріліс функцисы мына формуламен анықталады.
қатесінің өзгеру графигінің түрінде анықталады. Бұл жағдайда тұйықталған жүйенің беріліс функцисы мына формуламен анықталады. 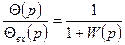
ал бастапқы шарт мына қатынасты ескеру арқылы қайта есептеледі.