Координатний метод на площині

Основні поняття і теореми

Програму розробив

Доцент Баран Олег Іванович

Варіант 12.09.2010

Миколаїв 2010

ПЛАНІМЕТРІЯ

Теореми, аксіоми, означення.

Необхідна і достатня умови.

Доведення теореми від супротивного.

Пряма лінія, промінь, відрізок, кути і їх вимірювання.

Перпендикуляр коротше похилої, а відрізок коротше ламаної.

Кути з паралельними сторонами. Кути з взаємно перпендикулярними сторонами.

Паралельні прямі, аксіома паралельності, ознаки паралельності прямих.

Теорема Фалеса. Застосування теореми Фалеса до розв’язування задач. Поділ відрізка у заданому відношенні. Поділ відрізка у середньому і крайньому відношенні (Золотий поділ відрізка).

Стандартний прямокутник. Подати геометричне доведення тотожностей:

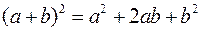та .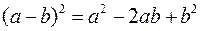

Ізопериметрична задача. Задача Дідони.

Елементи теорії графів. Проблема чотирьох фарб.

ТРИКУТНИКИ

Залежності між сторонами трикутника.

Ознаки рівності трикутників.

В трикутнику проти більшого кута лежить більша сторона.

Сума кутів трикутника (Перша теорема Піфагора).

Висоти, медіани та бісектриси трикутника, їх означення та головні властивості. Обчислення медіан, бісектрис та висот трикутника через його сторони:

, , .

, , .

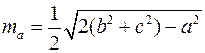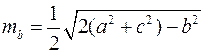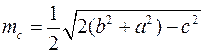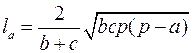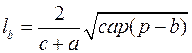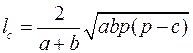Теорема про те, що висоти (медіани, бісектриси) трикутника перетинаються в одній точці. Медіани у точці перетину діляться у відношенні 2:1. Медіани розбивають трикутник на шість рівновеликих трикутників. Висоти трикутника у точці перетину утворюють шість кутів, попарно рівних кутам цього трикутника. Відрізки, що сполучають основи висот гострокутного трикутника, утворюють трикутник, бісектрисами якого є висоти даного.

Довести, що з усіх трикутників, вписаних у даний гострокутний трикутник, ортоцентричний (вершини якого співпадають з основами висот даного трикутника) має найменший периметр.

Обчислення довжин висот, медіан та бісектрис трикутника в залежності від його сторін.

Довести, що .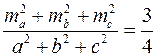

Середня лінія трикутника та її властивості.

Теорема про зовнішній кут трикутника та наслідки з неї.

Теорема про бісектрису внутрішнього та зовнішнього кутів трикутника. Кут між бісектрисами внутрішнього та зовнішнього кутів при одній вершині. Узагальнена теорема синусів:

.

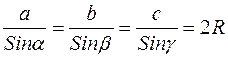Теорема косинусів:

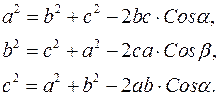
Вписане та описане коло трикутника. Зовнівписане коло.

Довести, що в довільному трикутнику мають місце співвідношення між його елементами:

1. ,

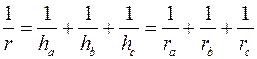2. ,

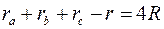3. ,

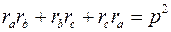4. ,

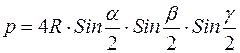5. ,

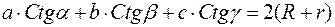6.

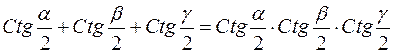
В прямокутному трикутнику сума діаметрів вписаного і описаного кіл дорівнює сумі катетів.

Довести, що в довільному трикутнику відстань d між центрами вписаного та описаного кіл визначається за формулою: 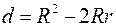(формула Ейлера). Наслідок: .

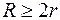Довести, що в довільному трикутнику відстань d між центрами вписаного і зовні вписаного кіл визначається за формулою: 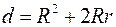, де r – радіус відповідного зовні вписаного кола.

Довести, що радіус вписаного в трикутник кола не перевищує половину радіусу описаного навколо нього кола. Прямокутні трикутники. Теорема Піфагора (пряма і обернена) та її наслідки. Різні способи доведення теореми Піфагора.

Довести, що в довільному прямокутному трикутнику куб його гіпотенузи більше суми кубів його катетів. В прямокутному трикутнику сума катетів дорівнює сумі діаметрів вписаного та описаного кіл. Середнє пропорційне та його зв’язок з прямокутним трикутником. Довести, що в прямокутному трикутнику бісектриса прямого кута ділить навпіл кут між медіаною та бісектрисою, проведеними до гіпотенузи.

Подібність трикутників. Ознаки подібності трикутників, ознаки подібності прямокутних трикутників.

Ортоцентр, центроїд (точка перетину медіан) і центр описаного навколо довільного трикутника кола лежать на одній прямій (пряма Ейлера). Центроїд ділить відрізок між центром вписаного кола і ортоцентром відповідно у відношенні 2:1.

Для довільного трикутника виконується рівність:

,

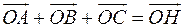де O – центр вписаного кола, а H – ортоцентр трикутника.

Середини сторін трикутника, основи його висот і середини відрізків висот, які сполучають його вершини з ортоцентром, лежать на одному колі (коло дев’яти точок, або коло Ейлера). Радіус цього кола вдвічі менший за радіус описаного навколо трикутника кола.

Коло Ейлера дотикається до вписаного і зовні вписаних кіл трикутника, а його центр лежить на прямій Ейлера і ділить відрізок між центром вписаного кола і ортоцентром навпіл.

Теорема Морлея.

Пряма та обернена теорема Менелая.

1. Якщо деяка пряма не проходить через вершини трикутника ABC, але перетинає його сторони BC, CA, AB або їх продовження відповідно в точках L, M, N, то має місце рівність:

.

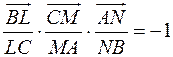2. Якщо точки L, M, N, які не співпадають з вершинами трикутника ABC, але лежать відповідно на його сторонах BC, CA, AB або їх продовження відповідно і має місце рівність:

,

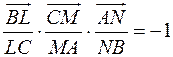то ці три точки лежать на одній прямій.

Пряма та обернена теорема Чеви.

Центр ваги суцільного чи каркасного однорідного трикутника.

Обчислення площі трикутника:

1) ;

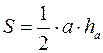2) ;

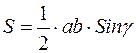3) ;

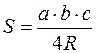4) ;

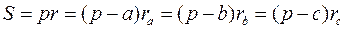5) ;

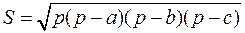6) ;

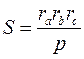7) ;

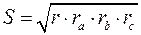8) ;

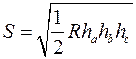9) ;

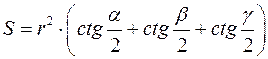10) ;

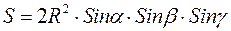11) ;

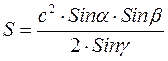12) ;

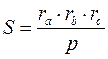13) ;

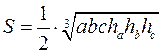14) ;

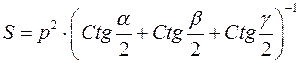15) ;

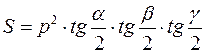16) 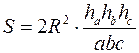та інші.

Довести, що сума відстаней від довільної точки в середині правильного трикутника до його сторін дорівнює його висоті. Довести, що сума відстаней від довільної точки основи рівнобедреного трикутника до його сторін, дорівнює висоті, яку проведено до бічної сторони. Довести, що точки симетричні ортоцентру гострокутного трикутника відносно його сторін лежать на описаному колі.

КОЛО І КРУГ

Означення кола, основні властивості. Дотичні до кола. Діаметр, перпендикулярний до хорди. Вимірювання кутів, пов’язаних з колом: центральні, вписані кути і кути, сторони яких (або їх продовження) перетинають коло.

Довжина кола, площа круга, сектора і сегмента.

Теорема про січну та дотичну.

Теорема про хорди в колі, які перетинаються (пряма і обернена теорема).

У всякому описаному навколо кола чотирикутнику суми довжин протилежних сторін рівні. У всякому вписаному в коло чотирикутнику суми протилежних його кутів рівні 180^о.

Для того, щоб навколо чотирикутника можна було описати коло, необхідно і достатньо, щоб добуток його діагоналей дорівнював сумі добутків його протилежних сторін (пряма і обернена теорема Птолемея).

Теорема Брахмагупти: площа вписаного в коло чотирикутника може бути обчислена за формулою:

,

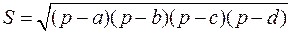а у випадку, коли коло одноразово і вписане в інший чотирикутник маємо:

.

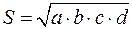Два різних кола не можуть мати більше двох спільних точок.

Площу описаного навколо кола многокутника можна обчислити за формулою:

,

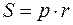де r – радіус кола, а р – його півпериметр.

Коло Аполлонія. Кола Форда.

Основи перпендикулярів, які опущені з довільної точки кола на сторони вписаного в нього трикутника, лежать на одній прямій (коло Симпсона).

МНОГОКУТНИКИ

Паралелограм, його властивості. Ознаки паралелограма. Діагоналі паралелограма в точці перетину діляться навпіл. Сума квадратів діагоналей паралелограма дорівнює сумі квадратів його сторін. Площа паралелограма та її обчислення.

Ромб і квадрат. Трапеція. Середня лінія трапеції та її властивості. Площа трапеції та її обчислення. Довести, що у довільній трапеції середини непаралельних сторін і діагоналей належить одній прямій. Довести, що у довільній трапеції середини основ, точка перетину її діагоналей та точка перетину бічних сторін належить одній прямій. Довести, що в довільній трапеції відрізок, який сполучає середини її діагоналей, дорівнює піврізниці основ трапеції і їм паралельний. Довести, що в довільній трапеції відрізок паралельний основі з кінцями на її бічних сторонах в точці перетину діагоналей ділиться навпіл.

В трапеції можна вказати чотири відрізки, які паралельні основам з кінцями на бокових сторонах, довжини яких дорівнюють відповідним середнім основ:

Відрізок, паралельний основі трапеції з кінцями на бічних сторонах	Довжина відповідного відрізка в залежності від довжин основ трапеції a і b	Назва відповідної середньої
Відрізок, який проходить через точку перетину діагоналей		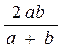середнє гармонічне
Відрізок, який ділить трапецію на дві подібні трапеції		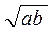середнє геометричне
Середня лінія трапеції		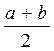середнє арифметичне
Відрізок, який ділить площу трапеції на дві рівновеликі частини		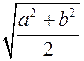середнє квадратичне
Співвідношення між відповідними середніми: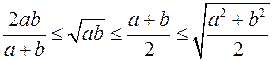

Площа чотирикутника обчислюється за формулою:

.

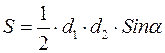Довести, що в опуклому чотирикутнику відрізки, які сполучають відповідно середини його протилежних сторін і середини діагоналей перетинаються в одній точці і діляться нею навпіл.

Сума кутів опуклого n-кутника. Теорема Варіньйона: відрізки, що сполучають послідовно середини сторін чотирикутника, утворюють паралелограм.

Рівновеликі многокутники.

ПЕРЕТВОРЕННЯ ПЛОЩИНИ

Вектори, їх властивості, операції над векторами.

Скалярний добуток векторів та його застосування.

Рух площини. Паралельний переніс, центральна і осьова симетрія, обертання, гомотетія.

КООРДИНАТНИЙ МЕТОД НА ПЛОЩИНІ

Декартові координати на площині. Віддаль між двома точками.

Координати векторів. Скалярний добуток векторів у координатній формі.

Рівняння прямої, яка проходить через дві задані точки. Рівняння прямої у відрізках. Кутовий коефіцієнт прямої, кут між двома прямими. Криві на площині, рівняння дотичної в даній точці.