Разложение определителя по строке или столбцу

Задание. Разложив по первой строке, вычислить определитель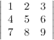

Решение.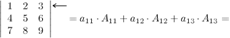

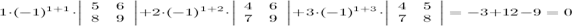
Ответ.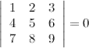

11. Пусть задана система n линейных уравнений с n неизвестными .

Начальный определитель , 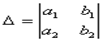. Если 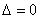то решений бесконечно. Если 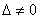решение 1. Найдем 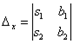и

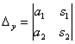
Корни уравнения находим по формулам: ,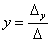

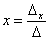12. Строчный ранг матрицы равен её столбцовому рангу. ранг матрицы – это максимальное количество линейно независимых строк. Или: ранг матрицы – это максимальное количество линейно независимых столбцов. Метод окаймляющих миноров:

1)Проверку миноров 2-го порядка начинаем с углового минора 2) Ищем не нулевой минор 3),

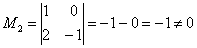значит, ранг матрицы не менее двух. 4) Приделываем ноги младшему коллеге 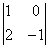,который будет входить во все рассматриваемые миноры высших порядков: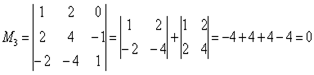

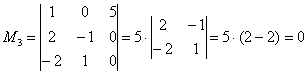
Продолжаем искать не нулевой!! Свешиваем ноги!

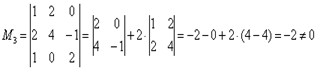Других миноров 3-го порядка, которые содержат младший ненулевой минор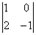– нет. И если бы «сине-коричневый» определитель тоже съел бублик, то 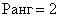. Проверим 4х4 так как минор=определитель= 0 Вывод: максимальный порядок ненулевого минора равен трём, значит, .

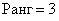13. Основные виды матриц:
Квадратная – (m=n)
Нулевая – все элементы = 0.
Транспонированная матрица — матрица В, полученная из исходной матрицы A заменой строк на столбцы.
Единичная – все элементы главной диагонали равны 1, все остальные 0.

14. Если имеется однородное линейное дифференциальное уравнение c постоянными коэффициентами р₀у⁽ⁿ⁾ + p₁y^(n-1) + … + p_ny = 0,

то алгебраическое уравнение p₀λⁿ + p₁λ^n-1 + … + p_n = 0

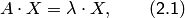называется его характеристическим уравнением.Собственный вектор — понятие в линейной алгебре, определяемое для квадратной матрицы или произвольного линейного преобразования как вектор, умножение матрицы на который или применение к которому преобразования даёт коллинеарный вектор è || .

называется собственным вектором матрицы 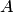. Число 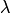в равенстве (2.1) называется собственным значением. Говорят, что собственный вектор 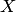соответствует (принадлежит) собственному значению 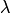. X – кол.строк??

15. Евкли́дово простра́нство - в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. пространство имеет размерность равную 3. Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. В трехмерном пространстве всегда можно расположить двумерное!

16.

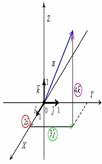
Радиус-вектор точки - это вектор с началом в начале координат, концом - в данной точке.Координаты радиус-вектора равны координатам точки.Скаля́рное произведе́ние иногда внутреннее произведение — операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Примеры применения??

17. 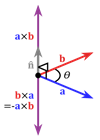Векторное произведение — это псевдовектор, перпендикулярный плоскости, но при этом в действительности является вектором. Геометрическая интерпретация -Обьяснение какого-либо математического процесса с помошью геометрических методов (Как пример геометрическая интерпритация функции - ее график).применения в физике - например, момент силы F, приложенной к точке М относительно точки О

18. Сме́шанное произведе́ние векторов — скалярное произведение вектора 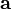на векторное произведение векторов 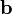и 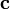: 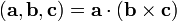. Условия компланарности векторов

• Три вектора компланарны если их смешанное произведение равно нулю.
• Три вектора компланарны если они линейно зависимы.

19. Полярная система координат