Предпосылки метода наименьших квадратов

В результате построения с помощью МНК уравнения регрессии получается не точное значение, а отличающееся от точного на некоторую величину :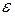

.

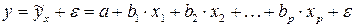После того как проведена оценка параметров модели, рассчитывая разности фактических и теоретических значений 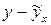можно получить оценки случайной составляющей 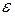. В задачу регрессионного анализа входит не только построение самой модели, но и исследование остаточных величин.

Необходимость этого объясняется тем, что при использовании МНК предполагалось, что остатки представляют собой независимые случайные величины и их среднее значение равно 0; они имеют одинаковую (постоянную) дисперсию.

Таким образом, исследование остатков предполагают проверку наличия следующих предпосылок МНК

Случайных характер остатков

Для проверки строится график зависимости остатков 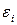от теоретических значений результативного признака. Если на графике получена горизонтальная полоса, то остатки 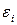представляют собой случайные величины и МНК оправдан, а теоретические значения 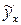хорошо аппроксимируют фактические значения y. Пример случайности остатков приведен на рисунке:

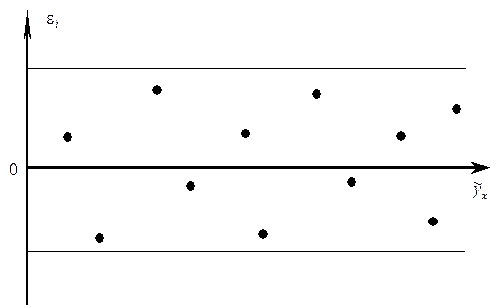
Возможны различные случаи зависимости остатков от теоретических значений 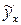. Приведем примеры

Нулевая средняя величина остатков, не зависящая от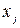

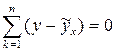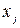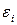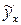Эта предпосылка означает, что . Это условие выполнимо для линейных моделей. Для определения независимость величины остатков от , как и в случае определения независимости от , строится график 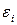от 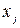. Если остатки на графике расположены в виде горизонтальной полосы, то они независимы от значений 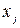. Если же зависимость присутствует, то модель является неадекватной.

Гомоскедастичность

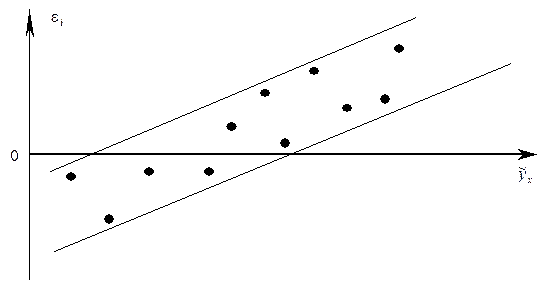
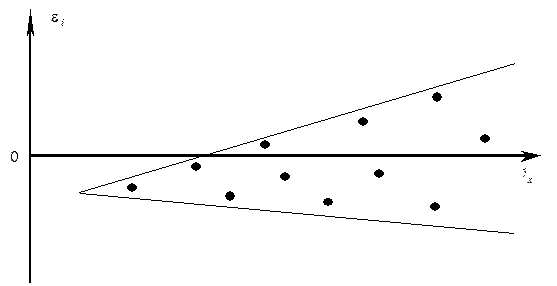
Гомоскедастичность остатков означает, что дисперсия каждого отклонения одинакова для всех значений x. Если это условие не соблюдается, то имеет место гетероскедастичность. Наличие гетероскедастичности можно наглядно видеть из поля корреляции (смотри рисунок).

Т.к. дисперсия характеризует отклонение то из рисунков видно, что в первом случае дисперсия остатков растет по мере увеличения x, а во втором – дисперсия остатков достигает максимальной величины при средних значениях величины x и уменьшается при минимальных и максимальных значениях x. Наличие гетероскедастичности будет сказываться на уменьшении эффективности оценок параметров уравнения регрессии. Наличие гомоскедастичности или гетероскедастичности можно определять также по графику зависимости остатков от теоретических значений .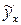

Отсутствие автокорреляции остатков

Под автокорреляцией остатков понимают зависимость распределения значений остатков 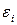друг от друга. Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений. Оценить эту зависимость можно вычислив коэффициент корреляции между этими остатками по формуле, аналогичной (6)

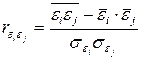. (10)

Если этот коэффициент окажется существенно отличным от нуля, то остатки автокоррелированны.

Пример. Проверить для уравнения регрессии, полученного ранее, выполнение предпосылок МНК.

Вычисляем теоретические значения по уравнению регрессии полученному ранее, а остатки по формуле 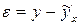и записываем в таблицу

Номер предприятия
, (%)
, (%)
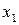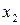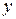, (тыс. ру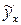б.)
, (тыс. руб.)	5,79	11,31	19,07	27,87
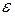, (тыс. руб.)	0,21	-0,31	-0,07	0,13

Теперь для проверки случайного характера остатков построим график их зависимости от теоретических значений .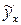

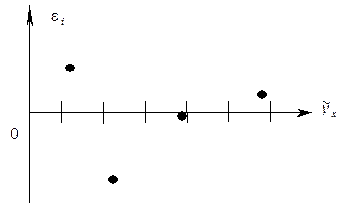
Хотя по четырем точкам судить трудно, но в целом можно сделать вывод, что остатки распределены случайно. Из этого же рисунка можно сделать вывод о гомоскедастичности остатков, т. к. дисперсия каждого отклонения одинакова для всех значений x.

Вычислим теперь величину суммарного отклонения:

.

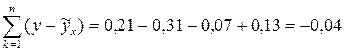По малости этой величины можно сделать вывод о практически нулевой средней величине остатков.

Коэффициент автокорреляции остатков находим по следующим рядам данных:

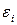, (тыс. руб.)	-0,31	-0,07	0,13
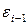, (тыс. руб.)	0,21	-0,31	-0,07

;

;

;

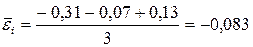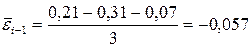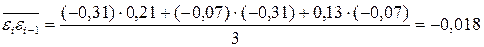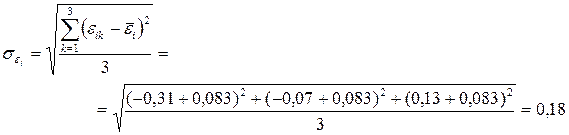
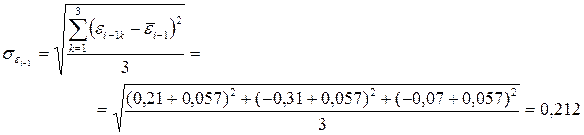
Отсюда находим

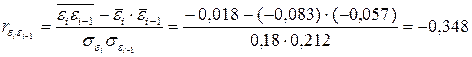
Коэффициент корреляции не так велик, и его можно считать приемлемым. Таким образом мы установили, что у нас были все предпосылки к тому, чтобы применять МНК и линейное уравнение регрессии к исходным данным.