Выбор осей координат. Углы Крылова (корабельные углы). Кинематические уравнения корабельного носителя на волнении

Вращательным движением твердого тела вокруг неподвижной точки называется такое его движение, при котором одна точка твердого тела или неизменно с ним связанная остается неподвижной относительно выбранной системы отсчета. Его еще называют сферическим движением, поскольку траектория любой точки тела лежит на поверхности сферы с центром в неподвижной точке. Примером такого движения служит волчок, у которого остается неподвижной точка опоры.

Число степеней свободы свободно движущегося в пространстве твердого тела равно шести. Если во время движения тела одна его точка остается неподвижной, то число степеней свободы такого тела при его вращении вокруг этой неподвижной точки будет равно трем и для оценки его положения необходимо задать три независимых параметра. Сделать это можно различными способами. Например, А.Н. Крылов в качестве таких параметров предложил так называемые корабельные углы, определяющие положение твердого тела (корабля) относительно системы координат, связанной своим началом с его центром тяжести (рис. 3.1).

Рис. 3.1

За оси неподвижной системы координат приняты CXYZ, а за оси жестко связанные с кораблем – Cxyz (рис. 3.1). Ось СХ направлена от кормы к носу корабля, ось CZ –к его правому борту, а ось CY образует с ними правую систему координат (вертикально вверх). Положение подвижной системы координат Cxyz, неизменно связанной с кораблем, относительно неподвижной CXYZ для каждого момента времени определяется тремя углами Крылова: углом дифферента , углом крена , углом рыскания (рис. 3.2).

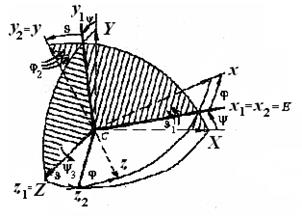
Рис. 3.2

Как видно на рис. 3.2, плоскость CXY пересекает плоскость Cxy по некоторой прямой 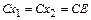, образующей угол с осьюCX и угол с осью Cx. Плоскость CYZ пересекает плоскость Cхy полинии Cy₁, образующей угол с осью Cy. Рассмотрим переход от системы CXYZ к системе Cxyz, выполненный с помощью трех поворотов.

Для совмещения системы CXYZ с системой Cxyz достаточно:

1) повернуть систему CXYZ вокруг третьей из координатных осей CZ на угол дифферента 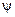, в результате чего получим систему Cx₁y₁z₁, причем Cz₁=CZ (рис. 3.3);

Рис. 3.3

2) повернуть систему 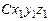вокруг первой из координатных осей 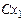на угол крена 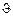, в результате чего получим систему 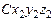, при этом 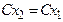(рис. 3.4);

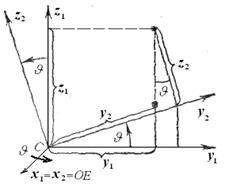
Рис. 3.4

3) повернуть систему вокруг второй из координатных осей на угол рыскания (рис. 3.5), в результате чего приходим к системе Cxyz .

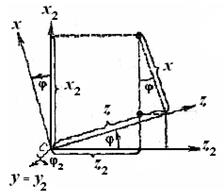
Рис. 3.5

Формулы преобразования координат связаны следующими соотношениями:

1) от CXYZ к 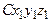(рис. 3.3)

X = x₁ cos y - y₁ sin y + 0 ,

Y =x₁ sin y + y₁ cos y + 0 , (3.1)

Z = 0 + 0 + z₁ ,

или в матричной форме:

[X] ={ a_3y}^т [x₁] , или 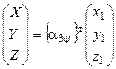, (3.2)

где 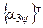- матрица, транспонированная к матрице 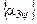, описывающей поворот системы CXYZ вокруг третьей координатной оси СZ на угол дифферента y,

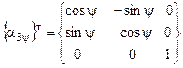; (3.3)

2) от системы 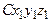к системе 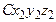(рис. 3.4)

x₁ = x₂ + 0 + 0 ,

y₁ = 0 + y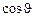₂ - z ₂ 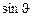, (3.4)

z₁ = 0 + y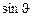₂ + z₂ ,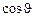

или в матричной форме

[x₁] = 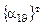[x₂] , или 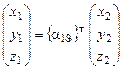, (3.5)

где 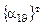– матрица, транспонированная к матрице 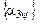, задающей преобразование поворота от осей системы 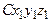к осям системы 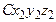вокруг первой из координатных осей 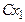на угол крена 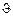, при этом = ,

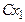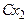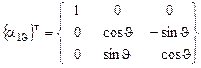; (3.6)

3) от системы координат 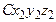к системе Cxyz (рис. 3.5)

x₂ = x cos j + 0 + z sin j,

y₂ = 0 + y + 0 , (3.7)

z₂ = -x sin j + 0 + z cos j,

или в матричной форме [x₂]= 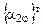[x], или

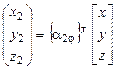. (3.8)

Причем поворотная матрица {a_2j }^т – это матрица, транспонированная к матрице { a_2j }, задающей преобразование поворота от осей системы 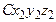к осям системы Cxyz на угол рысканияjвокруг второй из координатных осей 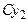= 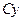, имеет вид

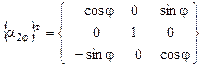. (3.9)

Для любой точки М тела с координатами x, y, z в подвижной системе координат, жестко связанной с ним, и с ее же координатами X, Y, Z – в неподвижной системе координат можно установить взаимосвязь проекций вектора точки 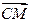на оси двух систем координат,

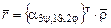, (3.10)

или в матричном виде

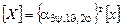или 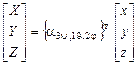, (3.11)

где углы Крылова являются некоторыми функциями времени: угол дифферента 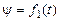,угол крена 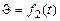,угол рыскания .

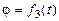Матрица 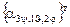транспонирована к матрице направляющих косинусов 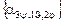, задающей преобразование поворота от осей неподвижной системы CXYZ к осям подвижной системы Cxyz, неизменно связанной с кораблем. Очевидно, что при движении тела координаты x, y, z остаются постоянными в отличие от координат X, Y, Z.

Подставляя в (3.2) соотношения (3.5) и (3.8), получаем:

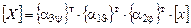. (3.12)

Сравнивая (3.11) и (3.12), находим, что искомая матрица 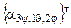является произведением трех поворотных матриц

=

=

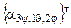
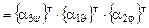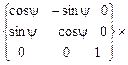
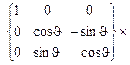
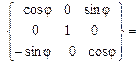
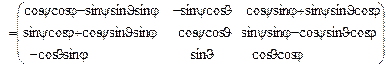.(3.13)

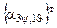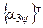
Подставляя в (3.2) соотношение (3.5), получаем промежуточное соотношение, которое может понадобиться в дальнейшем, [X] = [x₂]. Промежуточная поворотная матрица = 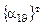находится как произведение двух матриц поворота:

=

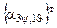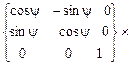
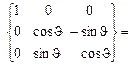
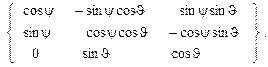= (3.13a)

Углы Эйлера

В тех случаях, когда угловая скорость вращения в одном направлении значительно больше, чем в двух других (генераторы, моторы, турбины, гироскопы), для определения положения тела в качестве трех независимых параметров выбирают три угла Эйлера: угол прецессииy (t),угол нутацииq (t) иугол ротации (собственного вращения) j (t). Их названия заимствованы из астрономии.

Чтобы задать эти углы, рассмотрим вращение твердого тела вокруг неподвижной точки О. Пусть даны некоторая система отсчета и связанная с ней неподвижная система координат ОXYZ, относительно которой движется твердое тело, и связанная с твердым телом система координат Оxyz, которая движется относительно первой (рис. 3.6 … 3.8). Это означает, что первая и вторая системы координат имеют общее начало O, а углы, образуемые осями Оxyz с осями ОXYZ, изменяются, т.е. система Оxyz
поворачивается вместе с твердым телом вокруг неподвижной точки О (рис. 3.5 … 3.8).

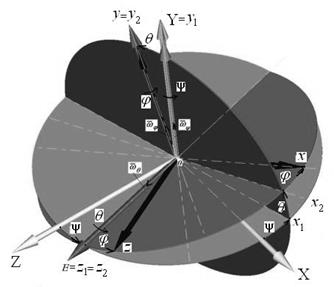Рис. 3.6

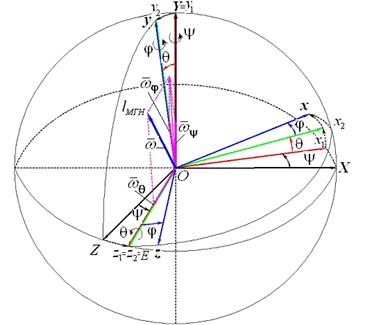
Рис. 3.7

Плоскость ОXZ (заштрихованный овал) пересекает плоскость Оxz (белый овал) по некоторой (рис. 3.8) прямой Оz⁽¹⁾ =Оz⁽²⁾ = OE, образующей угол y с неподвижной осью ОZ, и угол j с подвижной осью Оz, которая называется «линией узлов» ОЕ с единичным ортом . Кроме того, плоскость Оxz образует с плоскостью ОXZ угол q, равный углу между осями ОY и Оy.

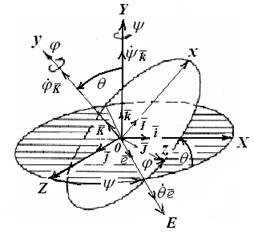
Рис. 3.8

Неподвижная ось ОY,вокруг которойповорачивается твердое тело на угол прецессииy, называется осью прецессии с единичным ортом .

Изменение угла нутацииq сопровождается вращением твердого тела вокруг линии узлов Оz₁ = Оz₂ = OE, называемой осью нутации.

Наконец, угол ротации (собственного вращения)j характеризует вращение тела вокруг оси Oy = Oy₂, называемой осью ротации (собственного вращения) с единичным ортом .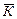

На рис 3.6 … 3.8 все углы положительные, т.е. против хода часовой стрелки, если смотреть на поворот тела с положительных направлений осей вращения OY, OE и Oy.

Движение твердого тела в любой момент времени полностью определяется положением подвижной связанной с твердым телом системы координат Оxyz относительно неподвижной системы координат ОXYZ, т.е. заданием кинематических уравнений вращения тела вокруг неподвижной точки О: угла прецессии 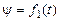,угланутации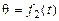иугларотации (собственного вращении) .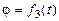