Равновесные процессы. Максимальная работа.

Рассмотрим процесс расширения системы от объема V₁ до объема V₂, происходящий путем уменьшения внешнего давления на некоторую конечную величину ΔР. За каждым уменьшением давления следует скачкообразное увеличение объема ΔV. Расширение продолжается до тех пор, пока система не перейдет в равновесное состояние, в которой будет оставаться до нового уменьшения давления, производимого извне (нижняя ломаная линия).

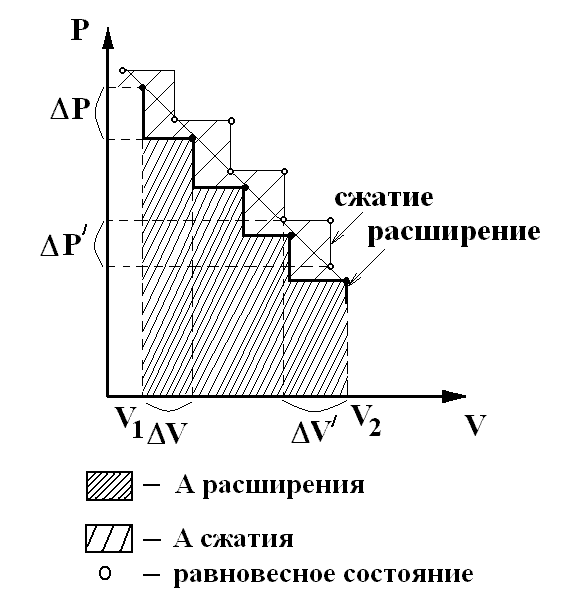
Произведем сжатие аналогичным путем: увеличивая давление на некоторую конечную величину ΔР’ объем системы уменьшается на ΔV’. Точки равновесного состояния процесса сжатия лежат на той же прямой, что и равновесные точки процесса расширения, но не совпадают с ними. (Верхняя ломаная линия). Из рисунка видно, что работа расширения, соответствующая площади трапеции под нижней ломаной линией меньше работы сжатия, соответствующей площади трапеции, ограниченной верхней ломаной линией. Такая картина реализуется в неравновесном процессе. Процесс расширения в рассмотренном примере не является равновесным, т.к. возврат системы в исходное состояние происходит по пути, отличному от прямого. Если процесс неравновесен и необратим, то в нем совершается меньшее количество работы, чем та, которую необходимо затратить, чтобы по окончании вернуть систему в исходное состояние.

Если же расширение провести последовательно и многократно на бесконечно малую величины dV, то процесс будет совершаться в состоянии, бесконечно близком к равновесию, поскольку бесконечно малому изменению объема dV будет соответствовать бесконечно малое изменение давления dР. Тогда ломанные кривые прямого и обратного пути станут бесконечно близки друг другу, а работа расширения станет максимальной. Такой процесс будет протекать бесконечно медленно, т. к. число скачков dV (dР) бесконечно велико, а время, необходимое для совершения каждого скачка конечно.

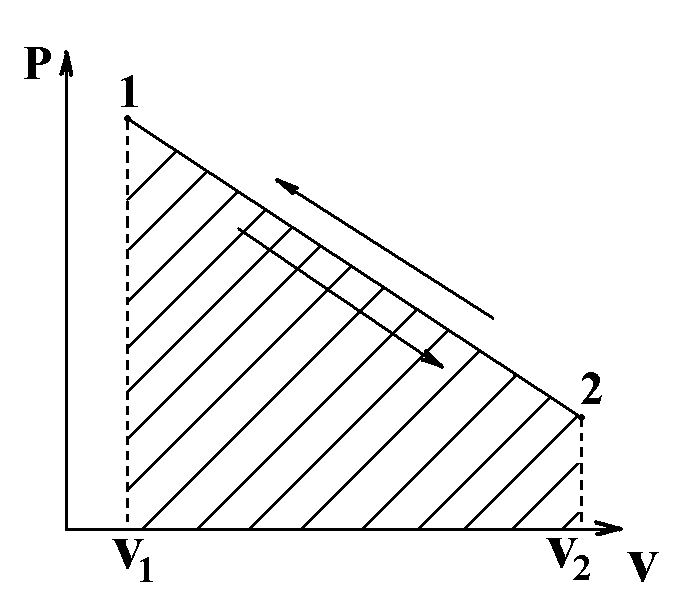
А_расш = А_сжат= А_макс

Процесс, который идет в прямом и обратном направлении через одни и те же состояния, бесконечно близкие к равновесию, называется равновесным.

Равновесная работа имеет максимальную величину по сравнению с работой неравновесного процесса. Это количество работы, которое необходимо затратить, чтобы вернуть систему в исходное состояние. А_макс является пределом, недостижимым на практике, но к которому стремятся приблизиться в реальных процессах. Примерами равновесных процессов являются идеальные механические процессы, протекающие без трения.

Обратимый процесс – такой равновесный процесс, который протекает в прямом и в обратном направлениях таким образом, что не только система, но и окружающая ее среда возвращается в исходное состояние и в результате не остается никаких изменений во всех телах, принимающих участие в процессе.

Равновесный т/д процесс является абстракцией, все реальные физические процессы в той или иной степени неравновесны. Примерами крайне неравновесных процессов является переход тепла от более нагретого тела к более холодному, расширение газа в пустоту, самопроизвольное смешение газов или жидкостей. Все эти процессы идут самопроизвольно, необратимо и быстро.

Уравнения состояния

Если система находится в равновесии, то ее свойства взаимосвязаны. Полная зависимость между свойствами системы может быть отражена различными уравнениями, но наибольшее значение имеют уравнения состояния, которые связывают P, T, V и состав или другие свойства. Эти уравнения не могут быть выведены ни из уравнений т/д, а получают их опытным путем или методами статистической физики.

Например:

А) Уравнение состояния идеального газа ( уравнение Менделеева-Клапейрона)

PV = nRT

Б) Уравнение состояния реального газа (уравнение Ван-дер-Ваальса)

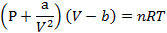
a – cродство к взаимному притяжению,

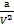- поправка на взаимное притяжение молекул,

в – поправка, учитывающая собственный объем молекул.

Наличие уравнений состояния приводит к тому, что для однозначной характеристики системы достаточно знать несколько параметров, а остальные можно вывести из уравнения состояния. Для простейшей системы, состоящей из одной фазы, основными параметрами состояния являются P, T, и V. В более сложных системах переменными в уравнения состояния могут входить концентрации компонентов и др.

Лекция №7