Катушки на постоянное напряжение
 |
Рассмотрим схему включения индуктивности на постоянное напряжение (рис. 11.3).
Запишем для этой схемы уравнение по второму закону Кирхгофа для независимой переменной – тока.
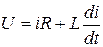. (11.1)
Ищем решение этого уравнения в виде суммы общего и частного решений, то есть в виде суммы свободной и принужденной составляющих
i =inp+iсв.
Находим принужденную составляющую в послекоммутационном установившемся режиме по закону Ома
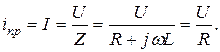
Так как для постоянного тока частота равна нулю, и, соответственно, индуктивное сопротивление будет равно нулю.
Для определения свободной составляющей решаем уравнение (11.1) при нулевых источниках
.
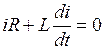Составляем характеристическое уравнение. Его можно составить двумя способами:
1) как уже рассматривали выше, делаем замену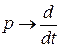 
, тогда
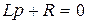, или 
;
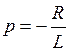2) записываем выражение для полного сопротивления цепи и приравниваем его нулю
,
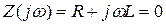заменяя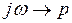 
, получим 
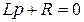, или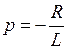 
.
Решение для свободной составляющей тока ищем в виде
.
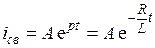Полный ток
.
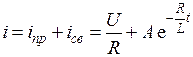
Постоянную интегрирования А находим, основываясь на независимых начальных условиях и законах коммутации.
До включения цепи тока в ней не было, то есть i(-0) = 0. Согласно второму закону коммутации в момент времени t = 0: i(+0) = i(-0) = 0, следовательно,
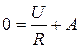. Отсюда 
.
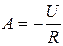В окончательном виде решение запишется
.
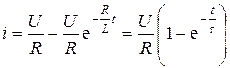Здесь через τ обозначили величину, обратную корню характеристического уравнения и имеющую противоположный знак:
.
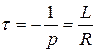Эта величина называется постоянной времени переходного процесса и характеризует скорость изменения тока во время переходного процесса. Количественно она равна времени, в течение которого ток изменится в е ≈ 2,7 раз.
Из полученного решения видно, что принужденная составляющая не зависит от времени и равна току установившегося режима. Свободная составляющая изменяется по экспоненциальному закону и имеет место все время, пока происходит накапливание энергии в катушке, что показано на рис. 11.4.
Теоретически переходной процесс длится бесконечно долго, так как экспонента стремится к нулю, достигая его только в бесконечности. Практически считается, что переходной процесс заканчивается за время t = (3…5)τ. Длительность переходного процесса определяется только структурой и параметрами электрической цепи.
Найдем закон изменения напряжения на индуктивности.
.
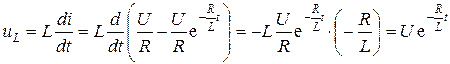Из полученного выражения видно, что индуктивное напряжение имеет только свободную составляющую. Действительно в установившемся режиме в цепи постоянного тока индуктивность представляет собой короткое замыкание, следовательно, напряжение на ней равно нулю.
 |
Из рис. 11.4 видно, что в первый момент переходного процесса индуктивное напряжение скачком увеличивается до величины общего напряжения U, а затем экспоненциально уменьшается до нуля.
 |
При отключении цепи, содержащей резистивный и индуктивный элементы, обычно одновременно эти элементы замыкают накоротко (рис. 11.5).
После отключения ток в короткозамкнутом контуре поддерживается за счет энергии, запасенной в катушке. Эта энергия рассеивается в резистивном элементе, и через некоторое время ток прекращается.
Уравнение состояния для данного контура можно записать по второму закону Кирхгофа
.
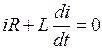Принужденная составляющая
.
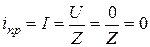Для определения свободной составляющей составим характеристическое уравнение
.
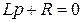Найдем корень характеристического уравнения
.
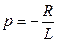Тогда свободная составляющая определится выражением
.
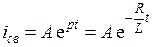Общий ток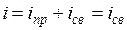 
.
Найдем постоянную интегрирования. До коммутации в цепи протекал ток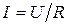 
, следовательно, согласно первому закону коммутации в первый момент переходного процесса t = 0 ток останется таким же:
.
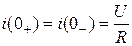Тогда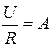 
,
ток переходного процесса определится выражением
.
 |
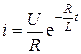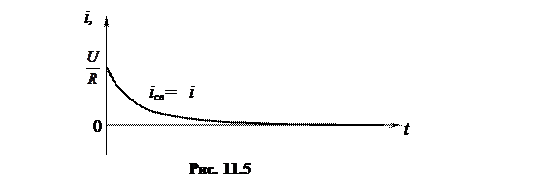Таким образом, при отключении индуктивности ток в течение переходного режима будет экспоненциально уменьшаться от максимального значения до нуля (рис. 11.5)