Абсолютная и условная сходимости рядов
Возьмем знакопеременный ряд 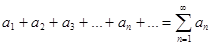 , где числа
, где числа 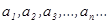 могут быть как положительными, так и отрицательными, причем их расположение в ряде произвольно.
могут быть как положительными, так и отрицательными, причем их расположение в ряде произвольно.
Рассмотрим ряд, составленный из абсолютных величин членов этого ряда 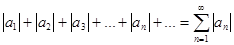 .
.
Определение: Знакопеременный ряд 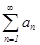 называется абсолютно сходящимся, если сходится ряд , составленный из модулей его членов
называется абсолютно сходящимся, если сходится ряд , составленный из модулей его членов 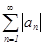 .
.
Из сходимости ряда 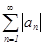 следует сходимость ряда
следует сходимость ряда 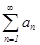 .
.
Определение: Если ряд 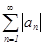 расходится, а сам знакопеременный ряд
расходится, а сам знакопеременный ряд 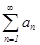 сходится, то он называется условно сходящимся.
сходится, то он называется условно сходящимся.
Так как ряд 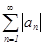 является рядом с положительными членами, то для исследования вопроса о его сходимости можно применять рассмотренные раннее признаки сходимости: признаки сравнения, Даламбера, интегральный и др.
является рядом с положительными членами, то для исследования вопроса о его сходимости можно применять рассмотренные раннее признаки сходимости: признаки сравнения, Даламбера, интегральный и др.
Пример 1: Исследовать ряд на абсолютную или условную сходимость: 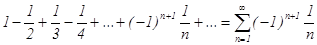 .
.
Решение: Составим ряд из модулей: 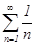 - это гармонический ряд, он расходится. Для исследования на сходимость исходного знакочередующегося ряда применим признак Лейбница:
- это гармонический ряд, он расходится. Для исследования на сходимость исходного знакочередующегося ряда применим признак Лейбница: 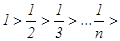 - первое условие выполнено;
- первое условие выполнено;
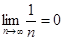 - второе условие выполнено.
- второе условие выполнено.
Таким образом , по признаку Лейбница ряд сходится.
Так как ряд из модулей расходится, а сам знакочередующийся ряд сходится, значит, он сходится условно.
Пример 2: Исследовать ряд на абсолютную или условную сходимость: 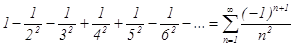 .
.
Решение: Составим ряд из абсолютных величин членов дан-
ного ряда: 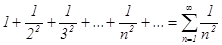 - это обобщенно-степенной ряд. Так как показатель степени
- это обобщенно-степенной ряд. Так как показатель степени 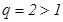 , то он сходится. Если сходится ряд из модулей, то знакочередующийся ряд сходится абсолютно.
, то он сходится. Если сходится ряд из модулей, то знакочередующийся ряд сходится абсолютно.
Степенные ряды
Определение: Выражение вида 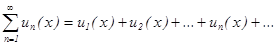 называется функциональным рядом.
называется функциональным рядом.
Определение:Степенным рядом называется функциональный ряд вида 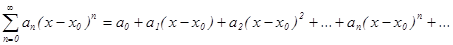 где x – независимая переменная,
где x – независимая переменная, 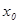 - фиксированное число,
- фиксированное число, 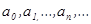 - постоянные коэффициенты.
- постоянные коэффициенты.
При 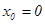 степенной ряд принимает вид:
степенной ряд принимает вид:

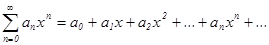 .
.
Определение: Областью сходимости степенного ряда называется совокупность всех значений x, при которых данный ряд сходится.
Нахождение области сходимости состоит из двух этапов:
1) Определяется интервал сходимости степенного ряда, т.е. интервал 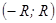 числовой оси, симметричный относительно точки x=0 и обладающий тем свойством, что при всех
числовой оси, симметричный относительно точки x=0 и обладающий тем свойством, что при всех 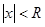 - ряд сходится. R – радиус сходимости находится по формуле:
- ряд сходится. R – радиус сходимости находится по формуле: 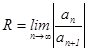 .
.
2) Исследуется сходимость ряда 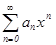 на концах интервала сходимости, т.е. в точках x= -R и x=R .
на концах интервала сходимости, т.е. в точках x= -R и x=R .
В зависимости от результатов исследования, область сходимости запишется одним из следующих неравенств:
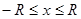 или
или 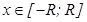 ;
;
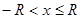 или
или 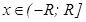 ;
;
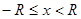 или
или 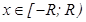 ;
;
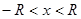 или
или 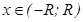 .
.
Для степенного ряда вида 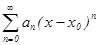 интервал сходимости имеет вид
интервал сходимости имеет вид 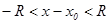 или
или 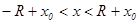 .
.
Пример 1:Найти область сходимости степенного ряда 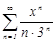 .
.
Решение: Найдем радиус сходимости степенного ряда .
В данном случае 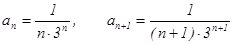 , тогда
, тогда
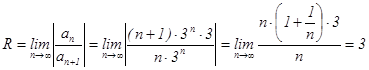
Запишем интервал сходимости: 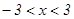 . Исследуем сходимость ряда на концах интервала.
. Исследуем сходимость ряда на концах интервала.
При 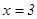 получаем числовой ряд
получаем числовой ряд 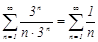 - это гармонический ряд, он расходится.
- это гармонический ряд, он расходится.
При 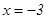 получаем знакочередующийся ряд
получаем знакочередующийся ряд 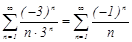 . Исследуем его на сходимость с помощью признака Лейбница:
. Исследуем его на сходимость с помощью признака Лейбница: 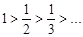 и
и 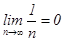
Оба условия признака Лейбница выполняются, следовательно ряд сходится.
Рассмотрим ряд из модулей его членов 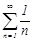 . Как показано выше данный ряд расходится. Отсюда можно сделать вывод, что при
. Как показано выше данный ряд расходится. Отсюда можно сделать вывод, что при 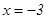 заданный степенной ряд сходится условно.
заданный степенной ряд сходится условно.
Ответ: Область сходимости ряда 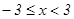 .
.
