Регресія. Метод найменших квадратів.
Частіше використовується так званий регресійний аналіз.
Регресією називається підгонка параметрів простої функції для найкращої апроксимації експериментальних даних(від латинського approximo – наближаюсь).
Для пошуку оптимальних значень параметрів функцій часто використовують метод найменших квадратів. Суть цього методу полягає в тому, щоб знайти такі коефіцієнти полінома, при яких сума квадратів відхилень(різниць між обчисленими та експериментальними значеннями функції) була мінімальною.
Нехай в результаті експерименту одержано таблицю значень функції y=f(x):
| x | x0 | x1 | x2 | … | xn |
| y | y0 | y1 | y2 | … | yn |
Необхідно апроксимувати цю функцію поліномом степені m (m<n)
Pm(x)=a0+a1x+a2x2+a3x3+… amxm..
За методом найменших квадратів знаходяться ті значення коефіцієнтів a0, a1, a2, …, am, для яких сума квадратів відхилень (невязки)
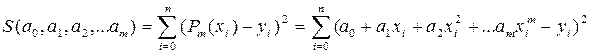
приймає мінімальне значення.
Використовуючи необхідні умови існування екстремуму функції декількох змінних, одержано систему рівнянь для визначення невідомих a0, a1, a2, …, am
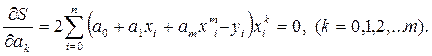
Якщо m=1, то функція y=f(x) апроксимується поліномом першої степені
P1(x)=a0+a1x.
Система рівнянь для визначення параметрів a0, a1 виглядає наступним чином
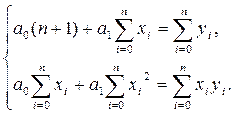
Якщо m=2, то функція y=f(x) апроксимується поліномом другої степені
P2(x)=b0+b1x+ b2x2.
Система рівнянь для визначення параметрів b0, b1, b2 виглядає наступним чином
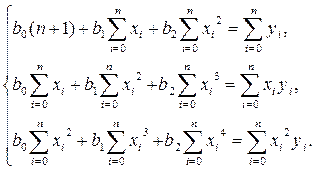
Для зручності при обчисленнях можна створити таблицю, яка наведена нижче:
| і | хі | хі2 | хі3 | хі4 | уі | хі уі | хі2 уі |
| х0 | х02 | х03 | х04 | у0 | х0 у0 | х02 у0 | |
| х1 | х12 | х13 | х14 | у1 | х1 у1 | х12 у1 | |
| … | … | … | … | … | … | … | … |
| … | … | … | … | … | … | … | … |
| n | хn | хn2 | хn3 | хn4 | уn | хn уn | хn2 уn |
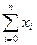 | 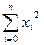 | 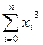 | 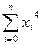 | 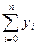 | 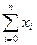 | 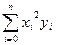 |
Лінійна регресія є найпростішою, але використовується частіше за інші види регресії. Суть її в знаходженні таких значень параметрів a і b, щоб пряма y = a + bx найкращим чином апроксимувала заданий набір точок.
Окрім апроксимації невідомої функції за допомогою прямої, використовується апроксимація за допомогою поліномів різного ступеня. Можна використовувати поліном будь-якого ступеня, Але не більший, ніж число точок у вибірці мінус один. При n=1отримаємо лінійну регресію. Частіше використовується поліноміальна регресія від другого до п’ятого ступеня.
Приклад 1
Дана таблиця, в якай вказана температура тіла в різні моменти часу. Необхідно знайти функцію, яка описує залежність температури від часу, тобто дозволяє знайти температуру тіла в заданий в момент часу.
| t | 0' | 10' | 20' | 30' |
| T | 60º | 90º | 80º | 20º |
Порядок виконання роботи
1 Знайти найпростішу функцію, яка при заданих значеннях аргументу (часу) приймала би ті самі значення функції (температури), що вказані в таблиці. Найпростішою функцією, зручною для обчислень, є поліном (ціла раціональна функція). Оскільки в таблиці вказані чотири значення функції, будемо шукати поліном третього ступеня.
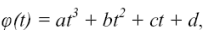
або
T = at3 + bt2 + ct + d.
2 Підібрати невідомі коефіцієнти a, b, c, d. Підберемо їх так, щоб при t = 0, 10, 20, 30 поліном прийняв відповідно значення T = 60, 90, 80, 20.
2.1 Підставимо послідовно значення t у поліном і прирівняємо відповідним значенням T. Отримаємо систему рівнянь:
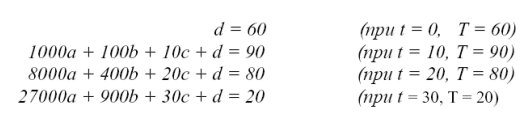
2.2 Розв’язати систему рівнянь і одержати
a = –1/600, b = –3/20, c = 14/3.
2.3 Записати формулу для полінома, вона буде мати вигляд:
T = – (1/600)t3 – (3/20)t2 + (14/3)t + 60.
3 Користуючись одержаним виразом, можна знайти температуру тіла в кожен момент часу від 0' до30'.
Наприклад, в момент t = 17' :
T = – (1/600)173– (3/20)172+ (14/3)17 + 60 = 87,8, тобто T= 87,8º.
Приклад 2 (Лінійна інтерполяція)
Потрібно побудувати лінійний інтерполяційний поліном для функції, яка задана у вигляді таблиці:
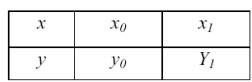
з такими чисельними значеннями
| х | ||
| у |
Порядок виконання роботи
1 Побудувати для двох вузлів інтерполяції формулу:
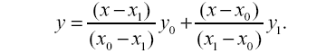
2 Підставити задані чисельні значення у формулу
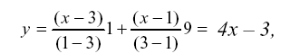
або
y = 4x – 3.
3 Побудувати графік функції, він має вигляд прямої лінії.
Приклад 3
Потрібно побудувати інтерполяційний квадратичний поліном для функції, яка задана у вигляді таблиці:
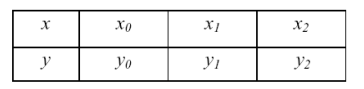
з такими чисельними значеннями:
| x | |||
| y |
Порядок виконання роботи
1 Побудувати для трьох вузлів інтерполяції квадратичний поліном у вигляді:
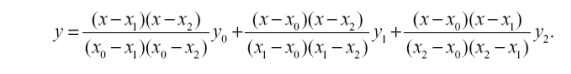
2 Підставити задані чисельні значення і отримати:
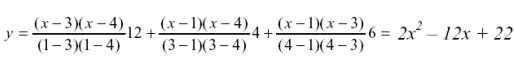
або y=2x2– 12x + 22.
3 Побудувати графік функції.
Приклад 4
Функція у=f(x) задана табличною у вузлах
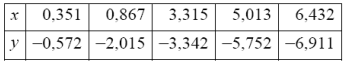
Порядок виконання роботи
1 Побудувати інтерполяційний лінійний сплайн.
1.1 Використати наступну кусково-лінійну апроксимацію
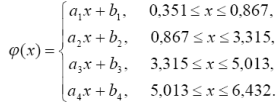
1.2 Побудувати систему рівнянь для визначення невідомих
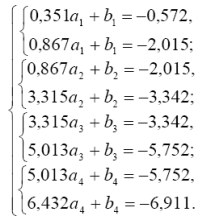
1.3 Із розв’язання систему одержано
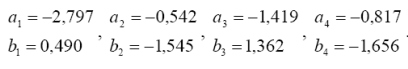
1.4 Лінійний сплайн матиме вигляд
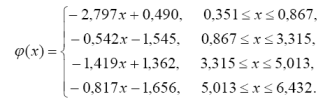
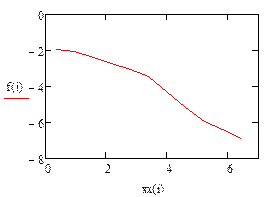
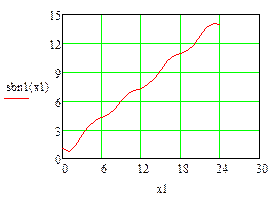
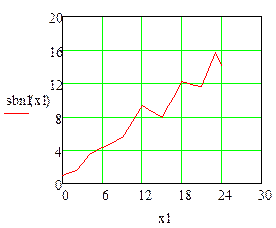
1.5 Побудувати графік лінійного сплайну (рис.1.1).
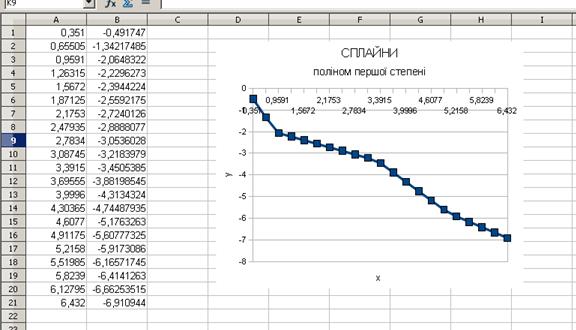
Рисунок 1.1– Графік лінійного сплайну (OPENOffice)
В системі MathCad графік інтерполяційного лінійного сплайна може бути представлено наступним чином
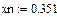 |
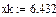 |
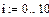 |
 |
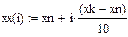 |
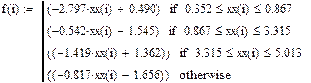 |
2 Побудувати інтерполяційний квадратичний сплайн.
2.1 Записати апроксимацію
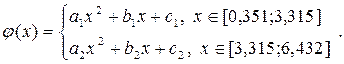
2.2 Скласти систему рівнянь
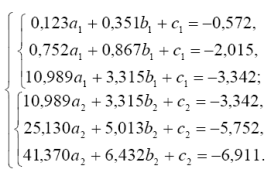
2.3 Розв’язуючи систему, одержимо
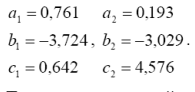
2.4 Квадратичний сплайн має вигляд
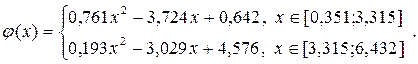
2.5 Побудувати графік квадратичного сплайну (рис.1.2).
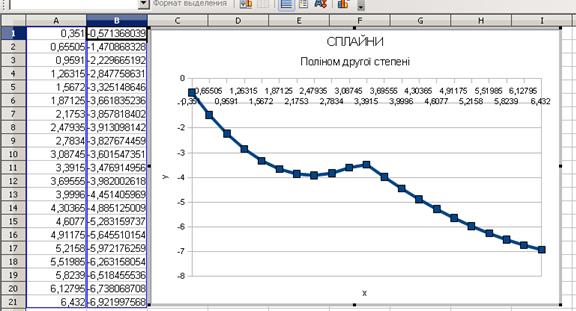
Рисунок 1.2 – Графік квадратичного (OPENOffice)
сплайну
3 Приклад обчислення лінійних, квадратичних, кубічних спалайнів в системі MathCad
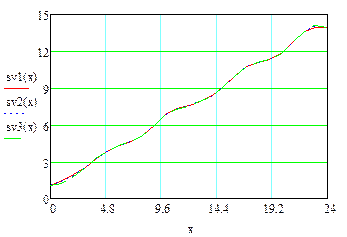 |
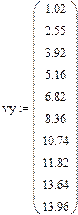 |
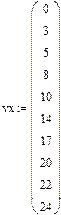 |
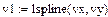 |
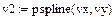 |
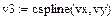 |
 |
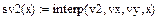 |
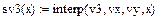 |
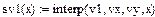 |
В–сплайнова інтерполяція
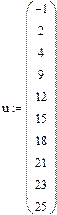 |
 |
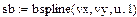 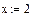 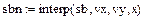 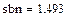 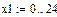 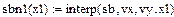 |
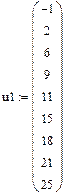 |
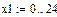 |
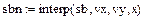 |
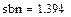 |
 |
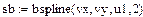 |
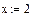 |
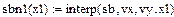
 |
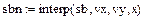 |
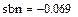 |
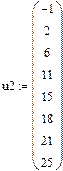 |
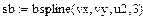 |
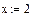 |
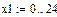 |
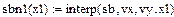 |
Приклад 5
Побудувати інтерполяційний поліном Лагранжа 4 степені 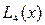 у вигляді лінійної комбінації
у вигляді лінійної комбінації 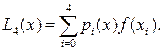
Порядок виконання роботи
1 Обчислити базисні поліноми
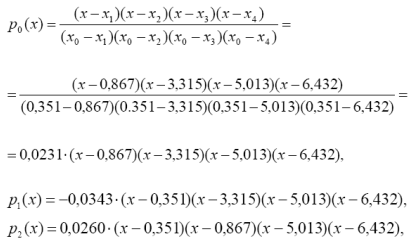
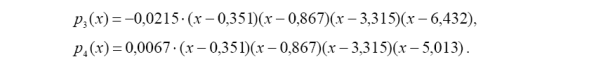
2 Інтерполяційний поліном Лагранжа матиме вигляд
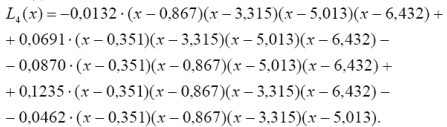
3 Обчислити значення полінома в точках х1 і х4
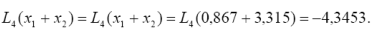
4 Побудувати графік полінома Лагранжа (рис. 1.3).
5 Представити на одному графіку інтерполяційні сплайни і поліном Лагранжа (рис.1.4).
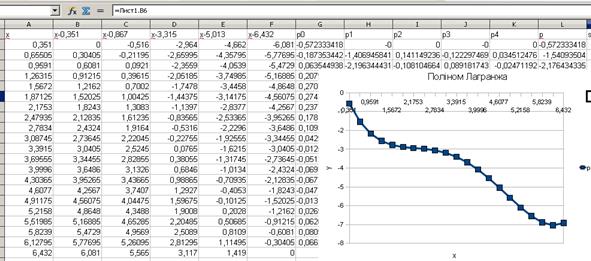
Рисунок 1.3 – Графік полінома Лагранжа
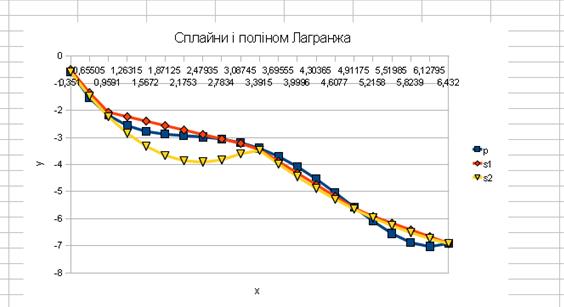
Рисунок 1.4 – Графік полінома Лагранжа і сплайнів
Приклад 6
Дана таблиця, яка отримана шляхом експерименту. Потрібно методом найменших квадратів знайти емпіричну формулу залежності у вигляді лінійної функції.
| x | ||||||||||
| y | 1,02 | 2,5 | 3,92 | 5,16 | 6,82 | 8,36 | 10,74 | 11,82 | 13,64 | 12,96 |
Порядок виконання роботи
1 Визначити значення Мх , Мху, Мхх, Му.
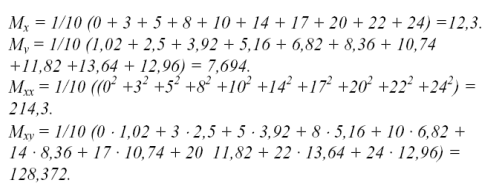
2 Знайти параметри a та b системи
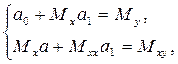
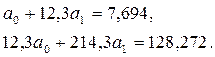
Розв’язавши систему, отримаємо: a = 1,109; b = 0,535. Лінійна функція має вигляд: y = 0,535x + 1,109.
Приклад 7
Функція задана у вигляді таблиці
| х | -3 | -1 | |||||
| у | 2,9 | 1,0 | -0,2 | -1,5 | -0,4 | 0,5 | 2,0 |
Порядок виконання роботи
1 Створити таблицю для додаткових обчислень
| і | хі | хі2 | хі3 | хі4 | уі | хі уі | хі2 уі |
| -3 | -27 | 2,9 | -8,7 | 26,1 | |||
| -1 | -1 | 1,0 | -1,0 | ||||
| -0,2 | |||||||
| -1,5 | -1,5 | -1,5 | |||||
| -0,4 | -0,8 | -1,6 | |||||
| 0,5 | 1,5 | 4,5 | |||||
| 8,0 | 32,0 | ||||||
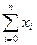 =6 =6 | 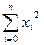 = 40 = 40 | 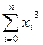 =72 =72 | 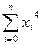 =436 =436 | 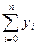 =4,3 =4,3 | 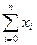 =-2,5 =-2,5 | 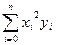 =60,5 =60,5 |
2 Записати систему рівнянь для знаходження коефіцієнтів а0 і а1 полінома першої степені
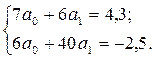
3 Знайти розв’язок системи рівнянь а0=0,766; а1=-0,177.
4 Записати поліном першої степені Р1(х)=0,766-0,177х.
5Записати систему рівнянь для апроксимуючого полінома другої степені відносно коефіцієнтів b0, b1, b2
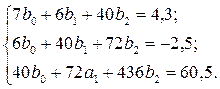
6 Обчислити коефіцієнти b0, b1, b2 полінома другої степені b0=-0,458; b1=-0,454; b2=0,256.
7 Записати поліном другої степені Р2(х)=-0,458-0,454х+0,256х2.
8 Побудувати графіки апроксимуючих поліномів першої і другої степені.
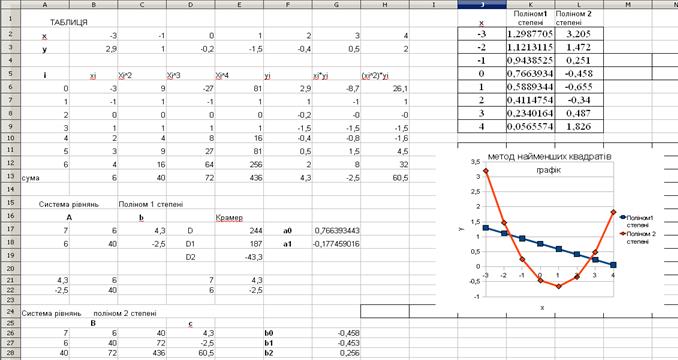
Рисунок 1. 5 – Результат побудови апроксимуючих поліномів
в Open Office.Calc
Контрольні питання
1 Дати визначення апроксимації.
2 Інтерполяція і екстраполяція.
3 Метод найменших квадратів.
4 Сплайн - апроксимація.
ЛАБОРАТОРНА РОБОТА № 2
